人教版数学九年级 上册24.2.2 圆的切线复习课 课件(15张)
文档属性
| 名称 | 人教版数学九年级 上册24.2.2 圆的切线复习课 课件(15张) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-26 09:58:29 | ||
图片预览


文档简介
切线的判定
.O
.O
.O
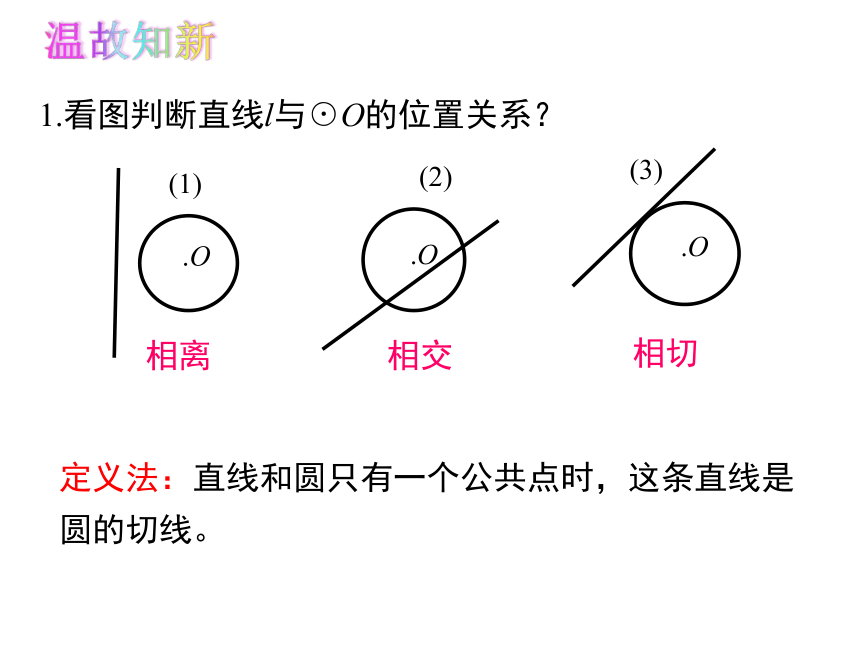
1.看图判断直线l与☉O的位置关系?
(1)
(2)
(3)
相离
相交
相切
定义法:直线和圆只有一个公共点时,这条直线是圆的切线。
2. ☉O的最大弦长为10,若圆心O到直线l的距离为d=5,
则直线l与☉O 的位置关系是 .
相切
数量关系法:圆心到直线的距离等于半径(即d=r)时,这条直线与圆相切。
O
A
B
C
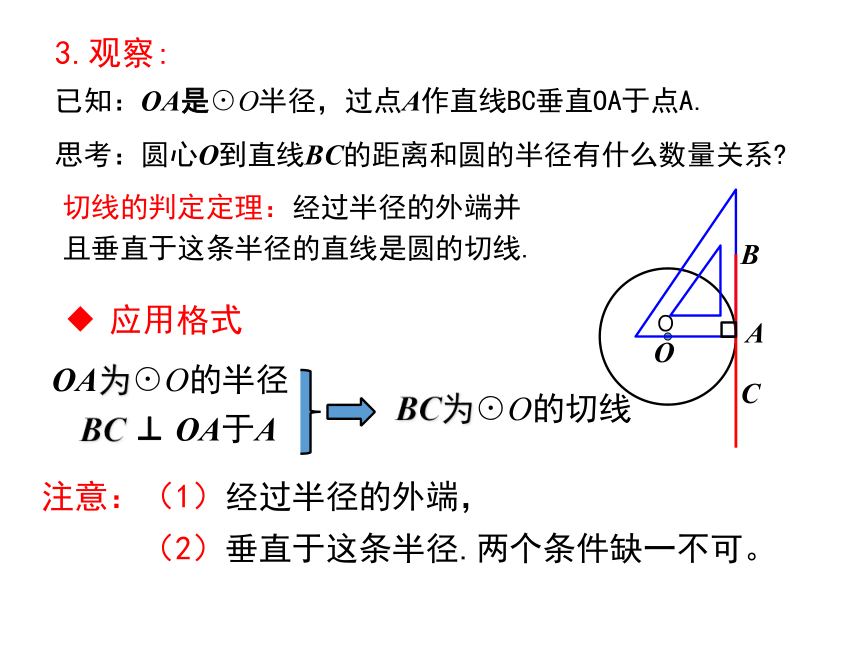
3.观察:
已知:OA是☉O半径,过点A作直线BC垂直OA于点A.
O
切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
BC ⊥ OA于A
BC为☉O的切线
应用格式
OA为☉O的半径
思考:圆心O到直线BC的距离和圆的半径有什么数量关系?
注意:(1)经过半径的外端,
(2)垂直于这条半径.两个条件缺一不可。
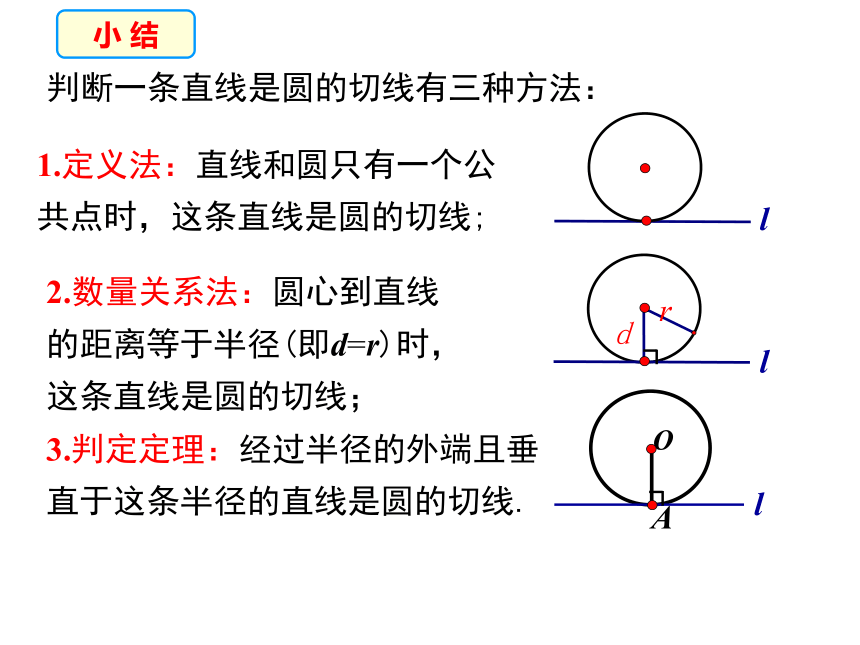
判断一条直线是圆的切线有三种方法:
1.定义法:直线和圆只有一个公共点时,这条直线是圆的切线;
2.数量关系法:圆心到直线的距离等于半径(即d=r)时,这条直线是圆的切线;
3.判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.
l
A
l
O
l
r
d
小 结
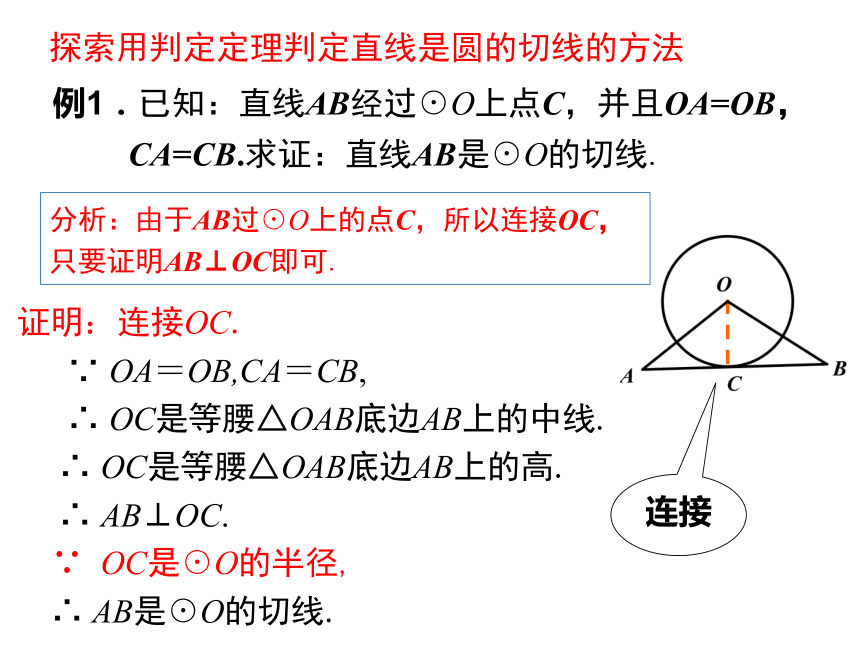
例1.已知:直线AB经过☉O上点C,并且OA=OB,
CA=CB.求证:直线AB是☉O的切线.
分析:由于AB过☉O上的点C,所以连接OC,只要证明AB⊥OC即可.
证明:连接OC.
∵ OA=OB,CA=CB,
∴ OC是等腰△OAB底边AB上的中线.
∴ OC是等腰△OAB底边AB上的高.
∴ AB⊥OC.
∵ OC是☉O的半径,
∴ AB是☉O的切线.
探索用判定定理判定直线是圆的切线的方法
连接
例2..如图,OA=OB=5,AB=8, ☉O的直径为6.
求证:直线AB是☉O的切线.
作垂直
分析:由于AB与☉O无交点,所以作OC⊥AB于点C,只要证明OC=半径即可.
∵ ☉O的直径为6
∴ OC是☉O的半径,
∴ AB是☉O的切线.
证明:作OC⊥AB于点C.
∵ OA=OB,
∴ OC是等腰△OAB底边AB上的高.
∴ OC是等腰△OAB底边AB上的中线
C
例1.如图,已知直线AB经过☉O上点C,并且OA=OB,CA=CB
求证:直线AB是☉O的切线.
例2.如图,OA=OB=5,AB=8, ☉O的直径为6.
求证:直线AB是☉O的切线.
作垂直
连接
证切线时辅助线的添加方法
(1) 有交点,连圆心,证垂直.
(2) 无交点,作垂直, 证半径.
证明圆切线的思路:先判断直线与圆是否有交点,
再确定添加辅助线的方法.
C
证明:连接OP.
∵AB=AC,∴∠B=∠C.
∵OB=OP,∴∠B=∠OPB,
∴∠OBP=∠C.
∴OP∥AC.
∵PE⊥AC,
∴PE⊥OP.
∵OP是☉O的半径
∴PE为☉O的切线.
1.如图,△ABC中,AB=AC,以AB为直径的☉O 交
边BC于P,PE⊥AC于E. 求证:PE是☉O的切线.
O
A
B
C
E
P
证明:作OE⊥CD于点E.
∵ DA是☉O 的切线
∴DA⊥OA.
∵ DO平分∠ADC
∴OE=OA
∵OE是☉O的半径
∴CD为☉O的切线.
2.如图,AB是☉O的直径,DA切☉O于点A,DO平分∠ADC。 求证:CD是☉O的切线。
3.如图,AB是☉O的直径,BC⊥AB于点B,连接OC,
弦AD?OC求证:CD是☉O的切线
证明:连接OD.
∵OA=OD,∴∠A=∠ADO.
∵OC∥AD.
∴∠COB=∠A,∠COD=∠ADO,
∴∠COB=∠COD.
∵OB=OD,OC=OC.
∵BC⊥AB,∴ ∠B=90°
∴ ∠CDO=90°,∴CD⊥OD,
∴CD是☉O的切线.
∵OD是☉O的半径
≌
O
A
B
C
E
P
圆切线证明的思路:
1.从复杂图形中抽象出基本的几何图形;
2.再判断有无交点
有交点,连半径,证垂直(证位置关系)
无交点,做垂直,证半径(证数量关系)
如图,△ABC内接于☉O,过A点作直线DE,∠BAE=∠C,试确定直线DE与☉O的位置关系,并证明你的结论。
.O
.O
.O
1.看图判断直线l与☉O的位置关系?
(1)
(2)
(3)
相离
相交
相切
定义法:直线和圆只有一个公共点时,这条直线是圆的切线。
2. ☉O的最大弦长为10,若圆心O到直线l的距离为d=5,
则直线l与☉O 的位置关系是 .
相切
数量关系法:圆心到直线的距离等于半径(即d=r)时,这条直线与圆相切。
O
A
B
C
3.观察:
已知:OA是☉O半径,过点A作直线BC垂直OA于点A.
O
切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
BC ⊥ OA于A
BC为☉O的切线
应用格式
OA为☉O的半径
思考:圆心O到直线BC的距离和圆的半径有什么数量关系?
注意:(1)经过半径的外端,
(2)垂直于这条半径.两个条件缺一不可。
判断一条直线是圆的切线有三种方法:
1.定义法:直线和圆只有一个公共点时,这条直线是圆的切线;
2.数量关系法:圆心到直线的距离等于半径(即d=r)时,这条直线是圆的切线;
3.判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.
l
A
l
O
l
r
d
小 结
例1.已知:直线AB经过☉O上点C,并且OA=OB,
CA=CB.求证:直线AB是☉O的切线.
分析:由于AB过☉O上的点C,所以连接OC,只要证明AB⊥OC即可.
证明:连接OC.
∵ OA=OB,CA=CB,
∴ OC是等腰△OAB底边AB上的中线.
∴ OC是等腰△OAB底边AB上的高.
∴ AB⊥OC.
∵ OC是☉O的半径,
∴ AB是☉O的切线.
探索用判定定理判定直线是圆的切线的方法
连接
例2..如图,OA=OB=5,AB=8, ☉O的直径为6.
求证:直线AB是☉O的切线.
作垂直
分析:由于AB与☉O无交点,所以作OC⊥AB于点C,只要证明OC=半径即可.
∵ ☉O的直径为6
∴ OC是☉O的半径,
∴ AB是☉O的切线.
证明:作OC⊥AB于点C.
∵ OA=OB,
∴ OC是等腰△OAB底边AB上的高.
∴ OC是等腰△OAB底边AB上的中线
C
例1.如图,已知直线AB经过☉O上点C,并且OA=OB,CA=CB
求证:直线AB是☉O的切线.
例2.如图,OA=OB=5,AB=8, ☉O的直径为6.
求证:直线AB是☉O的切线.
作垂直
连接
证切线时辅助线的添加方法
(1) 有交点,连圆心,证垂直.
(2) 无交点,作垂直, 证半径.
证明圆切线的思路:先判断直线与圆是否有交点,
再确定添加辅助线的方法.
C
证明:连接OP.
∵AB=AC,∴∠B=∠C.
∵OB=OP,∴∠B=∠OPB,
∴∠OBP=∠C.
∴OP∥AC.
∵PE⊥AC,
∴PE⊥OP.
∵OP是☉O的半径
∴PE为☉O的切线.
1.如图,△ABC中,AB=AC,以AB为直径的☉O 交
边BC于P,PE⊥AC于E. 求证:PE是☉O的切线.
O
A
B
C
E
P
证明:作OE⊥CD于点E.
∵ DA是☉O 的切线
∴DA⊥OA.
∵ DO平分∠ADC
∴OE=OA
∵OE是☉O的半径
∴CD为☉O的切线.
2.如图,AB是☉O的直径,DA切☉O于点A,DO平分∠ADC。 求证:CD是☉O的切线。
3.如图,AB是☉O的直径,BC⊥AB于点B,连接OC,
弦AD?OC求证:CD是☉O的切线
证明:连接OD.
∵OA=OD,∴∠A=∠ADO.
∵OC∥AD.
∴∠COB=∠A,∠COD=∠ADO,
∴∠COB=∠COD.
∵OB=OD,OC=OC.
∵BC⊥AB,∴ ∠B=90°
∴ ∠CDO=90°,∴CD⊥OD,
∴CD是☉O的切线.
∵OD是☉O的半径
≌
O
A
B
C
E
P
圆切线证明的思路:
1.从复杂图形中抽象出基本的几何图形;
2.再判断有无交点
有交点,连半径,证垂直(证位置关系)
无交点,做垂直,证半径(证数量关系)
如图,△ABC内接于☉O,过A点作直线DE,∠BAE=∠C,试确定直线DE与☉O的位置关系,并证明你的结论。
同课章节目录
