人教版数学九年级下册课件:29.2三视图(共24张PPT)
文档属性
| 名称 | 人教版数学九年级下册课件:29.2三视图(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-26 10:03:44 | ||
图片预览





文档简介
3.3 三视图
猜猜他们是什么关系?
从不同的方向观察同一物体时,可能看到不同的图形.
为了能完整确切地表达物体的形状和大小,必须从多方面观察物体。
从上面看
从正面看
从左边看
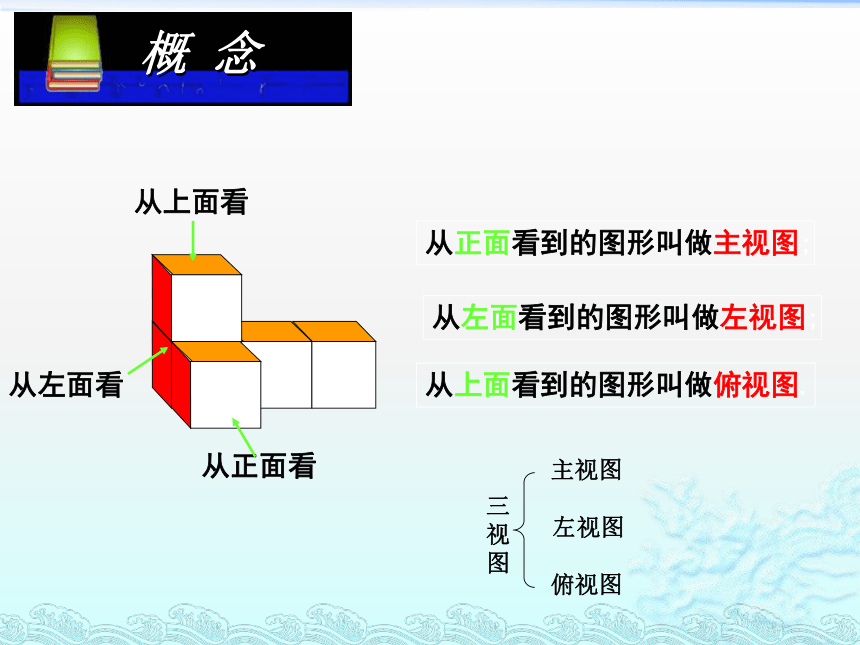
概 念
从正面看
从上面看
从左面看
从正面看到的图形叫做主视图;
从左面看到的图形叫做左视图;
从上面看到的图形叫做俯视图.
三视图
主视图
左视图
俯视图
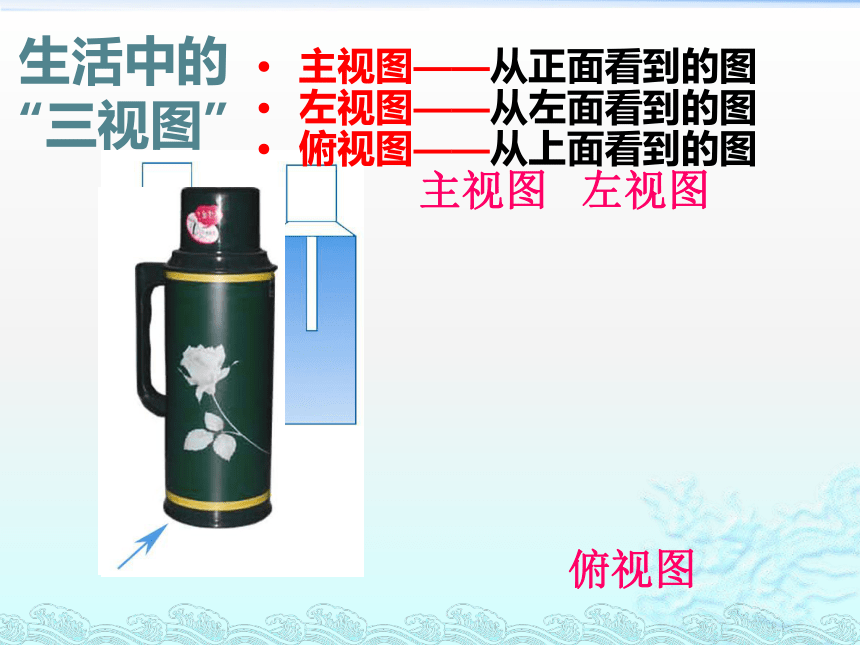
生活中的
“三视图”
俯视图
主视图
左视图
主视图——从正面看到的图
左视图——从左面看到的图
俯视图——从上面看到的图
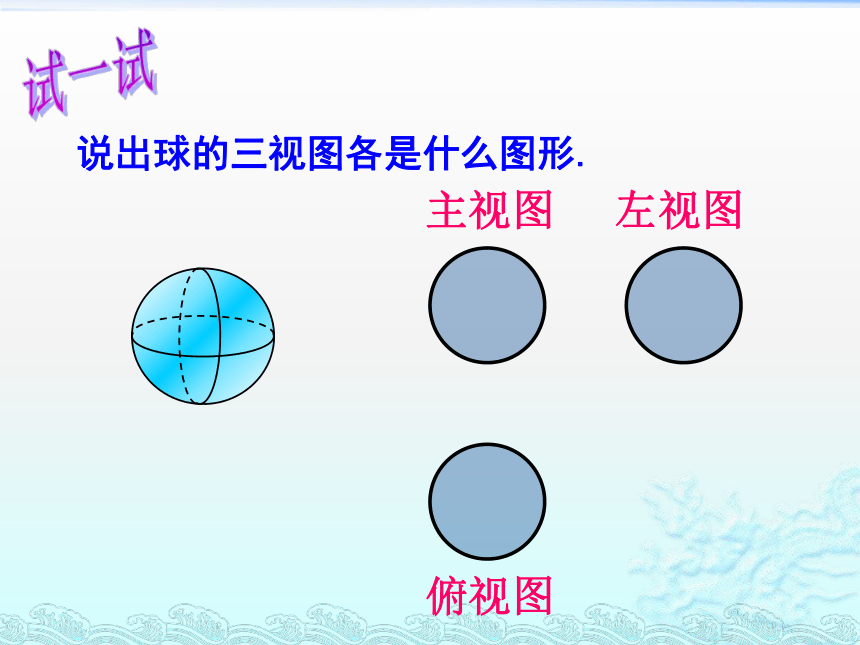
说出球的三视图各是什么图形.
试一试
俯视图
主视图
左视图
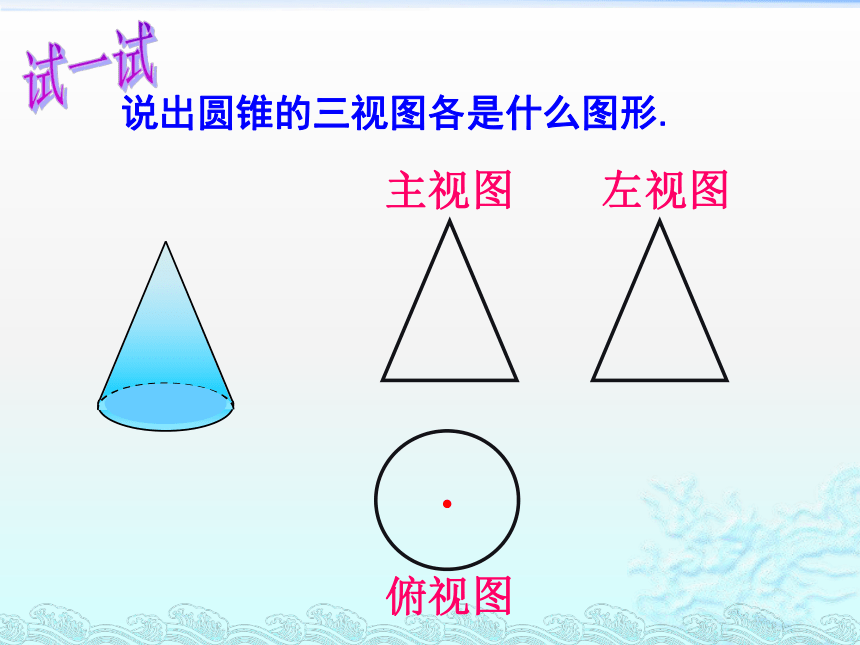
说出圆锥的三视图各是什么图形.
试一试
俯视图
主视图
左视图
说出正四棱锥的三视图各是什么图形.
试一试
俯视图
主视图
左视图
画三视图时,看得见的线都要画上去.
b
a
h
俯视图
b
主视图
a
h
长对正
高平齐
宽相等
左视图
h
b
b
a
h
a
任选两个视图
进行观察,
其中有没有
相等的线段
画三视图必须遵循的法则:
主视方向
例1
一个长方体的立体图如图3-18所示,请画它的三视图.
图3-18
已知一个直三棱柱的底面是等腰直角三角形,如图.请画出它的三视图.
学有所用
例2
由5个相同的小立方块搭成的几何体如图3-20所示,请画出它的三视图:
图3-20
长对正
高平齐
宽相等
左视图
俯视图
主视图
解: 所求三视图如图3-21.
图3-21
1.用4个小立方块搭成的几何体如图.请画出它的三视图.
2.用5块正方体搭成几何体,然后画出所搭几何体的三视图。
学有所用
你会了吗
1.一个直六棱柱和长方体如图所示放置.你能说出下面(a),(b),(c)三个视图分别是从哪个方向看到的吗?
(a) (b) (c)
A
B
C
D
2、由四个大小相同的小立方体搭成的几何体的左视图如图所示,则这个几何体的搭
法不能是( )
D
你会了吗
1.一个直六棱柱的主视图和俯视图如图所示,请补画它的左视图。
六棱柱
主视图
俯视图
左视图
主视图
俯视图
( 第1题 )
挑战提高
挑战提高
用4个完全相同的小立方块搭成一个主视图和俯视图都是如图所示图形的几何体,则不同的搭法有( )
A. 1种 B. 2种 C. 3种 D. 4种
一个几何体的视图是唯一的,但从视图反过来考虑几何体时,它有多种可能性。
B
体会.分享
说能出你这节课的收获和体验让大家与你分享吗?
主视方向
主视图
左视图
俯视图
宽相等
长对正
高平齐
例1
一个长方体的立体图如图3-18所示,请画它的三视图.
解: 所求三视图如图3-19.
图3-18
图3-19
主视图
左视图
俯视图
宽相等
长对正
高平齐
主视图——从正面看到的图
俯视图——从上面看到的图
左视图——从左面看到的图
画物体的三视图时,要符合如下原则:
位置:主视图 左视图
俯视图
大小:长对正,高平齐,宽相等.
畅所欲言:这节课我们主要学习了什么?
从不同方向观察同一物体时,可能看到不同的图形。
三视图
本节课给我们的启示:
从不同方向观察同一物体时,可能看到不同的图形,从不同角度分析同一件事或同一个人,结果可能也不一样。作为我们同学,要学会全面地评价每一个同学,我们今后看物、看人、看事都应从多角度、多方向分析,这样,我们就会发现许多美好的、闪光的东西,从而感受到我们生活是多么的美好!
作业:
1.作业本3.3
谢谢指导!
猜猜他们是什么关系?
从不同的方向观察同一物体时,可能看到不同的图形.
为了能完整确切地表达物体的形状和大小,必须从多方面观察物体。
从上面看
从正面看
从左边看
概 念
从正面看
从上面看
从左面看
从正面看到的图形叫做主视图;
从左面看到的图形叫做左视图;
从上面看到的图形叫做俯视图.
三视图
主视图
左视图
俯视图
生活中的
“三视图”
俯视图
主视图
左视图
主视图——从正面看到的图
左视图——从左面看到的图
俯视图——从上面看到的图
说出球的三视图各是什么图形.
试一试
俯视图
主视图
左视图
说出圆锥的三视图各是什么图形.
试一试
俯视图
主视图
左视图
说出正四棱锥的三视图各是什么图形.
试一试
俯视图
主视图
左视图
画三视图时,看得见的线都要画上去.
b
a
h
俯视图
b
主视图
a
h
长对正
高平齐
宽相等
左视图
h
b
b
a
h
a
任选两个视图
进行观察,
其中有没有
相等的线段
画三视图必须遵循的法则:
主视方向
例1
一个长方体的立体图如图3-18所示,请画它的三视图.
图3-18
已知一个直三棱柱的底面是等腰直角三角形,如图.请画出它的三视图.
学有所用
例2
由5个相同的小立方块搭成的几何体如图3-20所示,请画出它的三视图:
图3-20
长对正
高平齐
宽相等
左视图
俯视图
主视图
解: 所求三视图如图3-21.
图3-21
1.用4个小立方块搭成的几何体如图.请画出它的三视图.
2.用5块正方体搭成几何体,然后画出所搭几何体的三视图。
学有所用
你会了吗
1.一个直六棱柱和长方体如图所示放置.你能说出下面(a),(b),(c)三个视图分别是从哪个方向看到的吗?
(a) (b) (c)
A
B
C
D
2、由四个大小相同的小立方体搭成的几何体的左视图如图所示,则这个几何体的搭
法不能是( )
D
你会了吗
1.一个直六棱柱的主视图和俯视图如图所示,请补画它的左视图。
六棱柱
主视图
俯视图
左视图
主视图
俯视图
( 第1题 )
挑战提高
挑战提高
用4个完全相同的小立方块搭成一个主视图和俯视图都是如图所示图形的几何体,则不同的搭法有( )
A. 1种 B. 2种 C. 3种 D. 4种
一个几何体的视图是唯一的,但从视图反过来考虑几何体时,它有多种可能性。
B
体会.分享
说能出你这节课的收获和体验让大家与你分享吗?
主视方向
主视图
左视图
俯视图
宽相等
长对正
高平齐
例1
一个长方体的立体图如图3-18所示,请画它的三视图.
解: 所求三视图如图3-19.
图3-18
图3-19
主视图
左视图
俯视图
宽相等
长对正
高平齐
主视图——从正面看到的图
俯视图——从上面看到的图
左视图——从左面看到的图
画物体的三视图时,要符合如下原则:
位置:主视图 左视图
俯视图
大小:长对正,高平齐,宽相等.
畅所欲言:这节课我们主要学习了什么?
从不同方向观察同一物体时,可能看到不同的图形。
三视图
本节课给我们的启示:
从不同方向观察同一物体时,可能看到不同的图形,从不同角度分析同一件事或同一个人,结果可能也不一样。作为我们同学,要学会全面地评价每一个同学,我们今后看物、看人、看事都应从多角度、多方向分析,这样,我们就会发现许多美好的、闪光的东西,从而感受到我们生活是多么的美好!
作业:
1.作业本3.3
谢谢指导!
