苏科版八年级下册数学课件:第9章 中心对称图形复习(19张)
文档属性
| 名称 | 苏科版八年级下册数学课件:第9章 中心对称图形复习(19张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 645.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-26 00:00:00 | ||
图片预览





文档简介
初中数学八年级上册
(苏科版)
中心对称图形(复行四边形
矩形
菱形
正方形
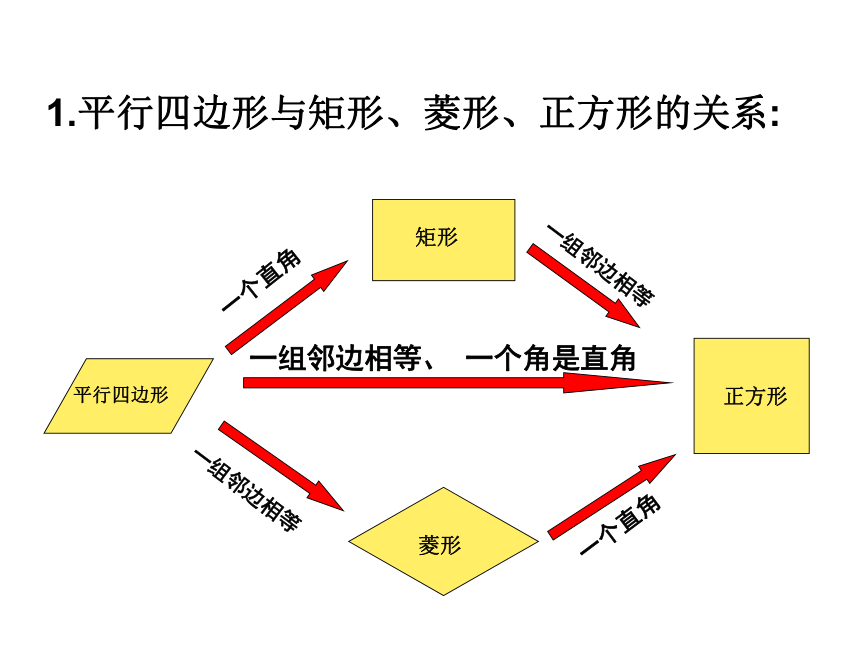
一组邻边相等
一个直角
一组邻边相等
一个直角
一组邻边相等、
一个角是直角
1.平行四边形与矩形、菱形、正方形的关系:
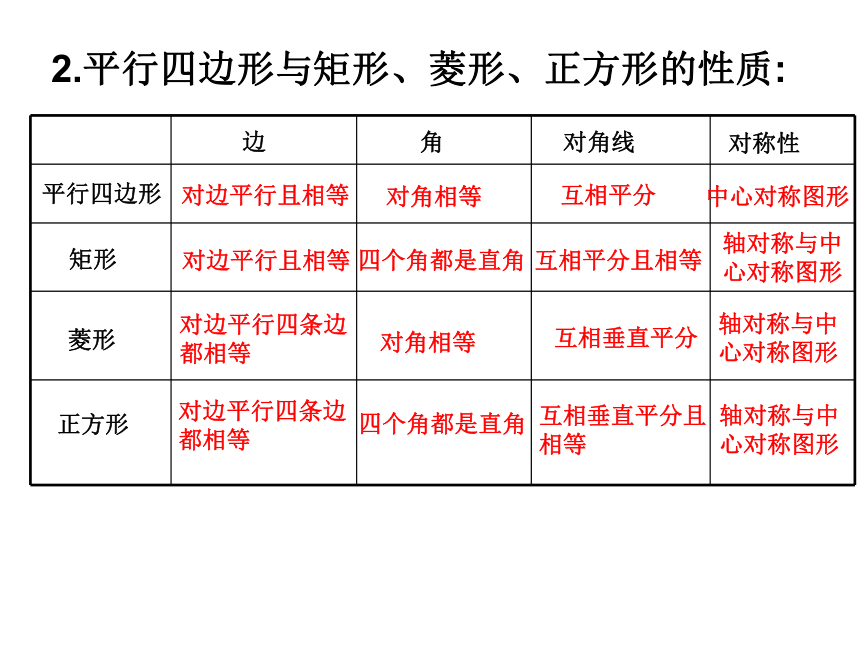
2.平行四边形与矩形、菱形、正方形的性质:
平行四边形
矩形
菱形
正方形
边
角
对角线
对称性
对边平行且相等
对边平行四条边都相等
对边平行四条边都相等
对边平行且相等
对角相等
对角相等
四个角都是直角
四个角都是直角
互相平分
中心对称图形
互相平分且相等
互相垂直平分
互相垂直平分且相等
轴对称与中心对称图形
轴对称与中心对称图形
轴对称与中心对称图形
平行四边形的判定:
(1)两组对边分别平行;
(2)两组对边分别相等;
(3)一组对边平行且相等;
(4)对角线互相平分.
矩形的判定:
(1)有三个角是直角;
(2)一个角是直角+平行四边形;
(3)对角线相等+平行四边形.
菱形的判定:
(1)四边都相等;
(2)一组邻边相等+平行四边形;
(3)对角线互相垂直+平行四边形.
知识结构
正方形:
(2)一组邻边相等+矩形;
(1)一组邻边相等+一个角是直角+平行四边形;
(3)一个角是直角+菱形.
知识结构
其它重要结论:
(1)关于旋转变换的性质:
①旋转前后的图形全等;
②对应点到旋转中心的距离相等;
③每一对对应点与旋转中心的连线所成的角彼此相等.
知识结构
其它重要结论:
关于三角形中位线
:
三角形的中位线平行于第三边,并且等于它的一半;
1.等腰三角形、等边三角形、矩形、平行四边形、正方形和圆这6种图形中,是中心对称图形的种数是
(
)
A、2
B、3
C、4
D、5
C
2.有一块长方形的田地,天地内有一口井,现在将这块土地平分给两户人家,要求两家合用这口井浇灌土地,请问该如何分?在图中画出分界线.(规定不能到对方的地里取水)
4.平行四边形ABCD周长为16cm,AC、BD相交于点O,
OE⊥AC交AC于E,则△DCE的周长是______
3.若一个平行四边形的一边长是8,一条对角线长是6,则另一条对角线a的取值范围
是_________.
10<a<22
8cm
5.A、B、C、D在同一平面内,从①AB∥CD;
②
AB=CD;③BC∥AD;④BC=AD,这四个
条件中任意选两个,能使四边形ABCD是平行
四边形的选法有(
)种.
A.3种
B.4种
C.5种
D.6种
6.
已知平行四边形两条邻边的高分别是6cm和
4cm它们的周长为40cm,则它的面积为--(
)
A.12cm2
B.24cm2
C.48cm2
D.72cm2
B
C
7.顺次连接对角线相等的四边形的各边中点所得的
四边形是
(
)A、平行四边形
B、矩形
C、菱形
D、正方形
C
8.
如果顺次连接四边形的各边中点所得的四边形是矩形,那么原来的四边形的对角线
(
)
A、互相平分
B、互相垂直
C、相等
D、相等且互相平分
B
9.已知:如图,在△ABC中,∠CAB=70?,将△ABC绕点A按逆时针方向旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′的度数为___.
1.已知:如图,四边形ABDE、ACFG是正方
形,EC、BG交于点M.
(1)
求证:BG=CE
(2)试猜想BG与CE的关系.
例题讲解
2.已知:如图,E为正方形ABCD的边BC的中
点,AE平分∠BAF.
求证:AF=BC+CF.
E
B
A
D
C
F
E
B
A
D
C
F
G
G
例题讲解
3.已知:四边形ABCD中,AB=2,CD=3,M、N分别
是AD,BC的中点,则线段MN的取值范围是
。
例题讲解
4.如图,在矩形ABCD中,AB=4cm,
AD=12cm,点P在AD边上以每秒1cm的速度
从点A向点D运动,点Q在BC边上,以每秒4cm
的速度从点C出发,在CB间往返运动,两个点
同时出发,当点P到达点D时停止(同时点Q也
停止),在这段时间内,t为何值时,ABQP是
矩形?
例题讲解
(苏科版)
中心对称图形(复行四边形
矩形
菱形
正方形
一组邻边相等
一个直角
一组邻边相等
一个直角
一组邻边相等、
一个角是直角
1.平行四边形与矩形、菱形、正方形的关系:
2.平行四边形与矩形、菱形、正方形的性质:
平行四边形
矩形
菱形
正方形
边
角
对角线
对称性
对边平行且相等
对边平行四条边都相等
对边平行四条边都相等
对边平行且相等
对角相等
对角相等
四个角都是直角
四个角都是直角
互相平分
中心对称图形
互相平分且相等
互相垂直平分
互相垂直平分且相等
轴对称与中心对称图形
轴对称与中心对称图形
轴对称与中心对称图形
平行四边形的判定:
(1)两组对边分别平行;
(2)两组对边分别相等;
(3)一组对边平行且相等;
(4)对角线互相平分.
矩形的判定:
(1)有三个角是直角;
(2)一个角是直角+平行四边形;
(3)对角线相等+平行四边形.
菱形的判定:
(1)四边都相等;
(2)一组邻边相等+平行四边形;
(3)对角线互相垂直+平行四边形.
知识结构
正方形:
(2)一组邻边相等+矩形;
(1)一组邻边相等+一个角是直角+平行四边形;
(3)一个角是直角+菱形.
知识结构
其它重要结论:
(1)关于旋转变换的性质:
①旋转前后的图形全等;
②对应点到旋转中心的距离相等;
③每一对对应点与旋转中心的连线所成的角彼此相等.
知识结构
其它重要结论:
关于三角形中位线
:
三角形的中位线平行于第三边,并且等于它的一半;
1.等腰三角形、等边三角形、矩形、平行四边形、正方形和圆这6种图形中,是中心对称图形的种数是
(
)
A、2
B、3
C、4
D、5
C
2.有一块长方形的田地,天地内有一口井,现在将这块土地平分给两户人家,要求两家合用这口井浇灌土地,请问该如何分?在图中画出分界线.(规定不能到对方的地里取水)
4.平行四边形ABCD周长为16cm,AC、BD相交于点O,
OE⊥AC交AC于E,则△DCE的周长是______
3.若一个平行四边形的一边长是8,一条对角线长是6,则另一条对角线a的取值范围
是_________.
10<a<22
8cm
5.A、B、C、D在同一平面内,从①AB∥CD;
②
AB=CD;③BC∥AD;④BC=AD,这四个
条件中任意选两个,能使四边形ABCD是平行
四边形的选法有(
)种.
A.3种
B.4种
C.5种
D.6种
6.
已知平行四边形两条邻边的高分别是6cm和
4cm它们的周长为40cm,则它的面积为--(
)
A.12cm2
B.24cm2
C.48cm2
D.72cm2
B
C
7.顺次连接对角线相等的四边形的各边中点所得的
四边形是
(
)A、平行四边形
B、矩形
C、菱形
D、正方形
C
8.
如果顺次连接四边形的各边中点所得的四边形是矩形,那么原来的四边形的对角线
(
)
A、互相平分
B、互相垂直
C、相等
D、相等且互相平分
B
9.已知:如图,在△ABC中,∠CAB=70?,将△ABC绕点A按逆时针方向旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′的度数为___.
1.已知:如图,四边形ABDE、ACFG是正方
形,EC、BG交于点M.
(1)
求证:BG=CE
(2)试猜想BG与CE的关系.
例题讲解
2.已知:如图,E为正方形ABCD的边BC的中
点,AE平分∠BAF.
求证:AF=BC+CF.
E
B
A
D
C
F
E
B
A
D
C
F
G
G
例题讲解
3.已知:四边形ABCD中,AB=2,CD=3,M、N分别
是AD,BC的中点,则线段MN的取值范围是
。
例题讲解
4.如图,在矩形ABCD中,AB=4cm,
AD=12cm,点P在AD边上以每秒1cm的速度
从点A向点D运动,点Q在BC边上,以每秒4cm
的速度从点C出发,在CB间往返运动,两个点
同时出发,当点P到达点D时停止(同时点Q也
停止),在这段时间内,t为何值时,ABQP是
矩形?
例题讲解
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
