人教版数学九年级下册27.3 位似图形坐标之间的关系 学案(无答案)
文档属性
| 名称 | 人教版数学九年级下册27.3 位似图形坐标之间的关系 学案(无答案) | 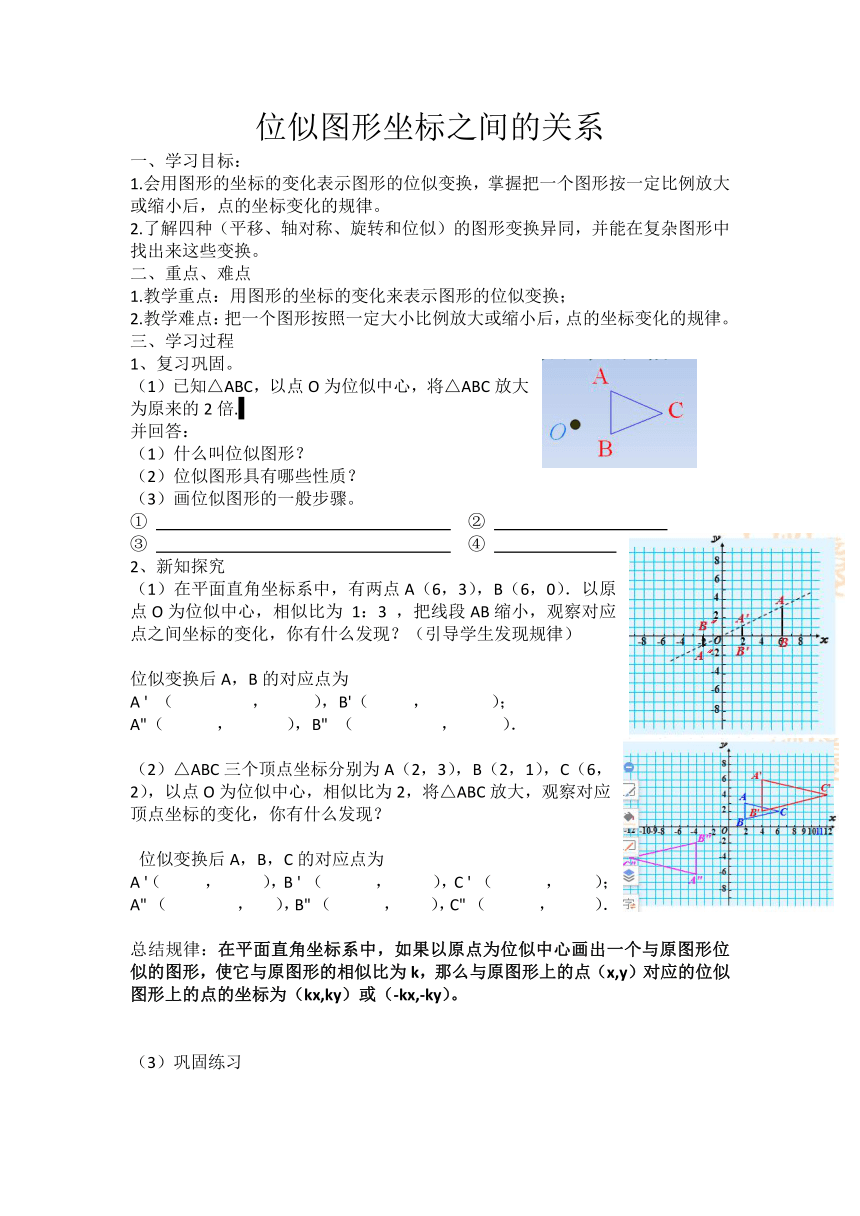 | |
| 格式 | zip | ||
| 文件大小 | 95.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-06 09:19:10 | ||
图片预览

文档简介
位似图形坐标之间的关系
学习目标:
1.会用图形的坐标的变化表示图形的位似变换,掌握把一个图形按一定比例放大或缩小后,点的坐标变化的规律。
2.了解四种(平移、轴对称、旋转和位似)的图形变换异同,并能在复杂图形中找出来这些变换。
二、重点、难点
1.教学重点:用图形的坐标的变化来表示图形的位似变换;
2.教学难点:把一个图形按照一定大小比例放大或缩小后,点的坐标变化的规律。
三、学习过程
1、复习巩固。
(1)已知△ABC,以点O为位似中心,将△ABC放大为原来的2倍.
并回答:
(1)什么叫位似图形?
(2)位似图形具有哪些性质?
(3)画位似图形的一般步骤。
①
②
③
④
2、新知探究
(1)在平面直角坐标系中,有两点A(6,3),B(6,0).以原点O为位似中心,相似比为
1:3
,把线段AB缩小,观察对应点之间坐标的变化,你有什么发现?(引导学生发现规律)
位似变换后A,B的对应点为
A
'
(
,
),B'(
,
);
A"(
,
),B"
(
,
).
△ABC三个顶点坐标分别为A(2,3),B(2,1),C(6,2),以点O为位似中心,相似比为2,将△ABC放大,观察对应
顶点坐标的变化,你有什么发现?
位似变换后A,B,C的对应点为
A
'(
,
),B
'
(
,
),C
'
(
,
);
A"
(
,
),B"
(
,
),C"
(
,
).
总结规律:在平面直角坐标系中,如果以原点为位似中心画出一个与原图形位似的图形,使它与原图形的相似比为k,那么与原图形上的点(x,y)对应的位似图形上的点的坐标为(kx,ky)或(-kx,-ky)。
巩固练习
1.如图,在平面直角坐标系中,以原点为位似中心,将△AOB扩大到原来的2倍,得到△OA′B′.若点B的坐标是(2,1),则点A′的坐标是( )
A.(4,2)
B.(-2,-1)
C.(-2,-4)
D.(-1,-2)
2.在平面直角坐标系中,已知点E(-4,2),F(-2,-2),以原点O为位似中心,相似比
为
,把△EFO缩小,则点E的对应点E′的坐标是( )
A.(-2,1)
B.(-8,4)
C.(-8,4)或(8,-4)
D.(-2,1)或(2,-1)
(4)例题:
如图,
三角形AB0的三个顶点的坐标分别为A(-2,4),B(-2,0),
O(0,0),画出它的一个以原点O为位似中心,相似比为
的位似图形.(分析:问题的关键是要确定位似图形各个顶点的坐标.)
A′(
-3,6
),
B′(
-3,0
),
O′
(
0,0
)
A′(
-3,6
),
B′(
-3,0
),
O′
(
0,0
)
(5)巩固练习
①
如图表示△AOB和把它缩小后得到的△COD,求它们的相似比。
∵点D的横坐标为2
点B的横坐标为5
∴相似比为
②在平面直角坐标系中,
四边形ABCD的四个顶点的坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出它的一个以原点O为位似中心,相似比为
的位似图形.
A′(
-3,3
),
B′(
-4,1
),
C′(
-2,0
),
D′(
-1,2
)
A"(
-3,3
),
B"(
-4,1
),
C"(
-2,0
),
D"(
-1,2
)
谈谈你的收获
课堂小结
布置作业
学习目标:
1.会用图形的坐标的变化表示图形的位似变换,掌握把一个图形按一定比例放大或缩小后,点的坐标变化的规律。
2.了解四种(平移、轴对称、旋转和位似)的图形变换异同,并能在复杂图形中找出来这些变换。
二、重点、难点
1.教学重点:用图形的坐标的变化来表示图形的位似变换;
2.教学难点:把一个图形按照一定大小比例放大或缩小后,点的坐标变化的规律。
三、学习过程
1、复习巩固。
(1)已知△ABC,以点O为位似中心,将△ABC放大为原来的2倍.
并回答:
(1)什么叫位似图形?
(2)位似图形具有哪些性质?
(3)画位似图形的一般步骤。
①
②
③
④
2、新知探究
(1)在平面直角坐标系中,有两点A(6,3),B(6,0).以原点O为位似中心,相似比为
1:3
,把线段AB缩小,观察对应点之间坐标的变化,你有什么发现?(引导学生发现规律)
位似变换后A,B的对应点为
A
'
(
,
),B'(
,
);
A"(
,
),B"
(
,
).
△ABC三个顶点坐标分别为A(2,3),B(2,1),C(6,2),以点O为位似中心,相似比为2,将△ABC放大,观察对应
顶点坐标的变化,你有什么发现?
位似变换后A,B,C的对应点为
A
'(
,
),B
'
(
,
),C
'
(
,
);
A"
(
,
),B"
(
,
),C"
(
,
).
总结规律:在平面直角坐标系中,如果以原点为位似中心画出一个与原图形位似的图形,使它与原图形的相似比为k,那么与原图形上的点(x,y)对应的位似图形上的点的坐标为(kx,ky)或(-kx,-ky)。
巩固练习
1.如图,在平面直角坐标系中,以原点为位似中心,将△AOB扩大到原来的2倍,得到△OA′B′.若点B的坐标是(2,1),则点A′的坐标是( )
A.(4,2)
B.(-2,-1)
C.(-2,-4)
D.(-1,-2)
2.在平面直角坐标系中,已知点E(-4,2),F(-2,-2),以原点O为位似中心,相似比
为
,把△EFO缩小,则点E的对应点E′的坐标是( )
A.(-2,1)
B.(-8,4)
C.(-8,4)或(8,-4)
D.(-2,1)或(2,-1)
(4)例题:
如图,
三角形AB0的三个顶点的坐标分别为A(-2,4),B(-2,0),
O(0,0),画出它的一个以原点O为位似中心,相似比为
的位似图形.(分析:问题的关键是要确定位似图形各个顶点的坐标.)
A′(
-3,6
),
B′(
-3,0
),
O′
(
0,0
)
A′(
-3,6
),
B′(
-3,0
),
O′
(
0,0
)
(5)巩固练习
①
如图表示△AOB和把它缩小后得到的△COD,求它们的相似比。
∵点D的横坐标为2
点B的横坐标为5
∴相似比为
②在平面直角坐标系中,
四边形ABCD的四个顶点的坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出它的一个以原点O为位似中心,相似比为
的位似图形.
A′(
-3,3
),
B′(
-4,1
),
C′(
-2,0
),
D′(
-1,2
)
A"(
-3,3
),
B"(
-4,1
),
C"(
-2,0
),
D"(
-1,2
)
谈谈你的收获
课堂小结
布置作业
