人教高中数学必修二3.2.2-直线的两点式方程 课件(30张ppt)
文档属性
| 名称 | 人教高中数学必修二3.2.2-直线的两点式方程 课件(30张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 10:13:45 | ||
图片预览











文档简介
(共31张PPT)
3.2.2 直线的两点式方程
形式
条件
直线方程
应用范围
点斜式
直线过点(x0,
y0),
且斜率为k
斜截式
在y轴上的截距为b,且斜率为k
不含与x轴垂直的直线
不含与x轴垂直的直线
知识回顾:
若已知直线经过两点定点P1(x1,
y1),P2(x2,
y2),
存在斜率,然后求出直线的斜率,
在上一节我们学习了已知直线上一定点P0(x0,
y0)和直线的斜率k,可以用点斜式表示直线方程:
何求直线的方程呢?
可根据已知两点的坐标,
又如
先判断是否
也就是说,已知两点坐标也能表示直线方程.
利用点斜式求直线方程.
这节课我们就来学习用两点坐标来表示直线方程.
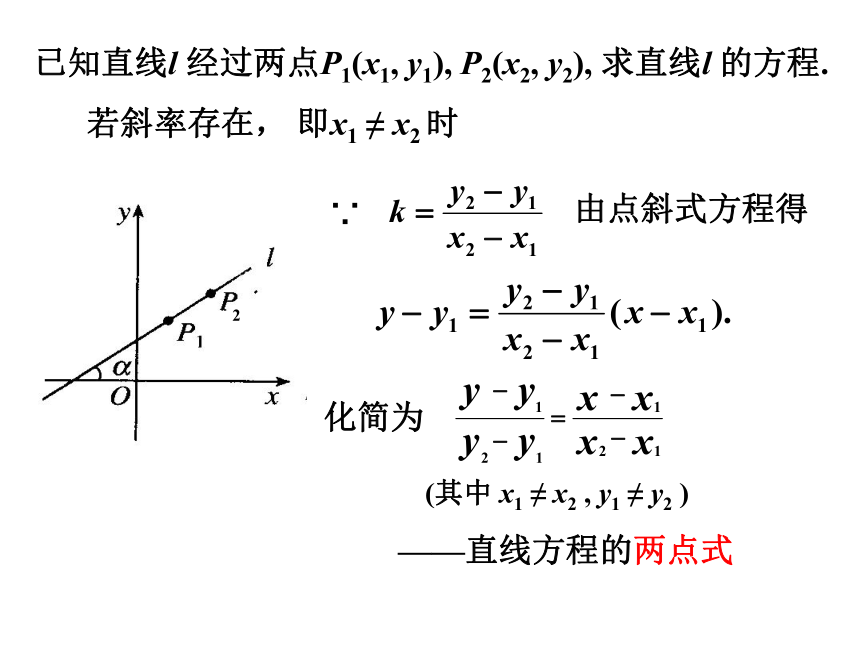
已知直线l
经过两点P1(x1,
y1),
P2(x2,
y2),
求直线l
的方程.
——直线方程的两点式
化简为
由点斜式方程得
∵
2
(其中
x1
≠
x2
,
y1
≠
y2
)
若斜率存在,
即x1
≠
x2
时
直线方程的两点式:
若点P1(x1,
y1),
P2(x2,
y2)中有
x1
=
x2
,或
y1
=
y2
,
此时这两点的直线
的方程是什么?
l:
x
=
x1
l:
y
=
y1
完成课本p97练习题第1题.
例1
直线l与x轴的交点是A(a,
0),与y轴的交点是B(0,
b),其中a
≠
0,
b
≠
0
,
求直线l
的方程.
解:
这里
a叫做直线在
x
轴上的截距(横截距),
——
直线方程的截距式
b叫做直线在
y
轴上的截距(纵坐标).
x
y
O
A
B
l
直线方程的截距式:
注意:
截距可以取全体实数,但截距式方程中的截距,是指非零的实数
,
点的直线方程,
因此截距式方程不包括过原
不包括与坐标轴垂直的直线方程.
x
y
O
完成课本p97练习题第2、3题.
形式
条件
方程
点斜式
直线过定点P(x0,y0)且斜率为k
斜截式
直线斜率为k且在y轴上的截距为b
两点式
直线过两定点
P1(x1
y1),
P2(x2,
y2)
截距式
直线在y轴上截距为b,在x轴上的截距为a
解:
故直线AB的方程为
例2
三角形的顶点是A(-5,0)、B(3,-3)、
C(0,2),求这个三角形三边所在直线的方程。
直线AB过A(-5,0),B(3,-3)
由两点式:
即
直线BC过B(3,-3),C(0,2),
由斜截式:
得
得
故直线BC的方程为
直线AC过A(-5,0),C(0,2),
由截距式:
得
即
为AC直线的方程.
解:
变式:
三角形的顶点是A(-5,0)、B(3,-3)、
C(0,2),求(1)BC边上中线所在直线的方程;
(2)AB边上高线所在直线的方程;
(3)AC边上中垂线所在直线的方程.
(1)由已知得,
BC边的中点
∵BC边上的中线过点A、M
,
∴BC边上中线所在直线的方程为:
即
(2)由AB边上高线过C(0,2),
且垂直于AB,
得
AB边上高线所在直线的方程:
其中
解:
变式:
三角形的顶点是A(-5,0)、B(3,-3)、
C(0,2),求(1)BC边上中线所在直线的方程;
(2)AB边上高线所在直线的方程;
(3)AC边上中垂线所在直线的方程.
(2)由AB边上高线过C(0,2),
且垂直于AB,
故AB边上高线所在直线的方程:
高线的斜率为
即
解:
变式:
三角形的顶点是A(-5,0)、B(3,-3)、
C(0,2),求(1)BC边上中线所在直线的方程;
(2)AB边上高线所在直线的方程;
(3)AC边上中垂线所在直线的方程.
(3)
∵AC边上中垂线过AC边的中点
且垂直于AC,
垂线的斜率为
∴AC边上中垂线所在直线的方程为:
即
例6.直线l
经过点(3,2),且在两坐标轴上的截距相等,
求直线
l
的方程.
因此直线
l
不与
x、y
轴垂直,斜率存在,且
k
≠0.
解法一:
由于直线
l
在两轴上有截距,
可设直线方程为
由题设可得
l
在
y
轴上有截距为
l
在
x
轴上有截距为
∴直线
l
的方程为
解:
另解:
∵
AB
边中线过
AB
边中点M
和△ABC
的重心
,
例4.直线l
经过点(3,2),且在两坐标轴上的截距相等,
求直线
l
的方程.
因此直线
l
不与
x、y
轴垂直,斜率存在,且
k
≠0.
解法一:
由于直线
l
在两轴上有截距,
可设直线方程为
由题设可得
l
在
y
轴上有截距为
l
在
x
轴上有截距为
∴直线
l
的方程为
例4.直线l
经过点(3,2),且在两坐标轴上的截距相等,
求直线
l
的方程.
解法二:
由已知可设直线
l
方程为
则由直线l
经过点(3,2)得
∴
直线
l
的方程为
则直线l
经过点(0,0)
,
又直线l
经过点(3,2)
,
∴
直线
l
的方程为
综上所述直线
l
的方程为
解:
例
6.
解:
则由直线通过点(1,2),得
此时,a
=
2
,
x
y
P
o
解:
例
6.
可设直线
l
方程为:
令
得
即
令
得
即
正方向
即
解:
当且仅当
即
时,
故所求直线
l
方程为:
即
解:
由已知可设直线
l
方程为:
令
得
即
令
得
即
当且仅当
即
时,
此时所求直线方程为:
即
变式:
课堂练习
解:
小节:
1
两点式
2
截距式
解:
例5 求直线
的倾斜角的取值范围.
解:
分析:将直线的方程化为斜截式,得出直线的斜率,再由
斜率和倾斜角的关系,得出关于的一个三角不等式即可.
由直线的方程
得斜率
∵
∴
即
3.2.2 直线的两点式方程
形式
条件
直线方程
应用范围
点斜式
直线过点(x0,
y0),
且斜率为k
斜截式
在y轴上的截距为b,且斜率为k
不含与x轴垂直的直线
不含与x轴垂直的直线
知识回顾:
若已知直线经过两点定点P1(x1,
y1),P2(x2,
y2),
存在斜率,然后求出直线的斜率,
在上一节我们学习了已知直线上一定点P0(x0,
y0)和直线的斜率k,可以用点斜式表示直线方程:
何求直线的方程呢?
可根据已知两点的坐标,
又如
先判断是否
也就是说,已知两点坐标也能表示直线方程.
利用点斜式求直线方程.
这节课我们就来学习用两点坐标来表示直线方程.
已知直线l
经过两点P1(x1,
y1),
P2(x2,
y2),
求直线l
的方程.
——直线方程的两点式
化简为
由点斜式方程得
∵
2
(其中
x1
≠
x2
,
y1
≠
y2
)
若斜率存在,
即x1
≠
x2
时
直线方程的两点式:
若点P1(x1,
y1),
P2(x2,
y2)中有
x1
=
x2
,或
y1
=
y2
,
此时这两点的直线
的方程是什么?
l:
x
=
x1
l:
y
=
y1
完成课本p97练习题第1题.
例1
直线l与x轴的交点是A(a,
0),与y轴的交点是B(0,
b),其中a
≠
0,
b
≠
0
,
求直线l
的方程.
解:
这里
a叫做直线在
x
轴上的截距(横截距),
——
直线方程的截距式
b叫做直线在
y
轴上的截距(纵坐标).
x
y
O
A
B
l
直线方程的截距式:
注意:
截距可以取全体实数,但截距式方程中的截距,是指非零的实数
,
点的直线方程,
因此截距式方程不包括过原
不包括与坐标轴垂直的直线方程.
x
y
O
完成课本p97练习题第2、3题.
形式
条件
方程
点斜式
直线过定点P(x0,y0)且斜率为k
斜截式
直线斜率为k且在y轴上的截距为b
两点式
直线过两定点
P1(x1
y1),
P2(x2,
y2)
截距式
直线在y轴上截距为b,在x轴上的截距为a
解:
故直线AB的方程为
例2
三角形的顶点是A(-5,0)、B(3,-3)、
C(0,2),求这个三角形三边所在直线的方程。
直线AB过A(-5,0),B(3,-3)
由两点式:
即
直线BC过B(3,-3),C(0,2),
由斜截式:
得
得
故直线BC的方程为
直线AC过A(-5,0),C(0,2),
由截距式:
得
即
为AC直线的方程.
解:
变式:
三角形的顶点是A(-5,0)、B(3,-3)、
C(0,2),求(1)BC边上中线所在直线的方程;
(2)AB边上高线所在直线的方程;
(3)AC边上中垂线所在直线的方程.
(1)由已知得,
BC边的中点
∵BC边上的中线过点A、M
,
∴BC边上中线所在直线的方程为:
即
(2)由AB边上高线过C(0,2),
且垂直于AB,
得
AB边上高线所在直线的方程:
其中
解:
变式:
三角形的顶点是A(-5,0)、B(3,-3)、
C(0,2),求(1)BC边上中线所在直线的方程;
(2)AB边上高线所在直线的方程;
(3)AC边上中垂线所在直线的方程.
(2)由AB边上高线过C(0,2),
且垂直于AB,
故AB边上高线所在直线的方程:
高线的斜率为
即
解:
变式:
三角形的顶点是A(-5,0)、B(3,-3)、
C(0,2),求(1)BC边上中线所在直线的方程;
(2)AB边上高线所在直线的方程;
(3)AC边上中垂线所在直线的方程.
(3)
∵AC边上中垂线过AC边的中点
且垂直于AC,
垂线的斜率为
∴AC边上中垂线所在直线的方程为:
即
例6.直线l
经过点(3,2),且在两坐标轴上的截距相等,
求直线
l
的方程.
因此直线
l
不与
x、y
轴垂直,斜率存在,且
k
≠0.
解法一:
由于直线
l
在两轴上有截距,
可设直线方程为
由题设可得
l
在
y
轴上有截距为
l
在
x
轴上有截距为
∴直线
l
的方程为
解:
另解:
∵
AB
边中线过
AB
边中点M
和△ABC
的重心
,
例4.直线l
经过点(3,2),且在两坐标轴上的截距相等,
求直线
l
的方程.
因此直线
l
不与
x、y
轴垂直,斜率存在,且
k
≠0.
解法一:
由于直线
l
在两轴上有截距,
可设直线方程为
由题设可得
l
在
y
轴上有截距为
l
在
x
轴上有截距为
∴直线
l
的方程为
例4.直线l
经过点(3,2),且在两坐标轴上的截距相等,
求直线
l
的方程.
解法二:
由已知可设直线
l
方程为
则由直线l
经过点(3,2)得
∴
直线
l
的方程为
则直线l
经过点(0,0)
,
又直线l
经过点(3,2)
,
∴
直线
l
的方程为
综上所述直线
l
的方程为
解:
例
6.
解:
则由直线通过点(1,2),得
此时,a
=
2
,
x
y
P
o
解:
例
6.
可设直线
l
方程为:
令
得
即
令
得
即
正方向
即
解:
当且仅当
即
时,
故所求直线
l
方程为:
即
解:
由已知可设直线
l
方程为:
令
得
即
令
得
即
当且仅当
即
时,
此时所求直线方程为:
即
变式:
课堂练习
解:
小节:
1
两点式
2
截距式
解:
例5 求直线
的倾斜角的取值范围.
解:
分析:将直线的方程化为斜截式,得出直线的斜率,再由
斜率和倾斜角的关系,得出关于的一个三角不等式即可.
由直线的方程
得斜率
∵
∴
即
