北师大版高中数学必修一-4.1.1 函数与方程 课件(18张PPT)
文档属性
| 名称 | 北师大版高中数学必修一-4.1.1 函数与方程 课件(18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 793.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 00:00:00 | ||
图片预览





文档简介
普通高中课程标准实验教材数学1(必修)北师大版
第四章 函数应用
§1 函数与方程
1.理解函数零点的概念,领会函数零点与相应方程解的关系.(重点)
2.掌握零点存在的判定方法.(难点)
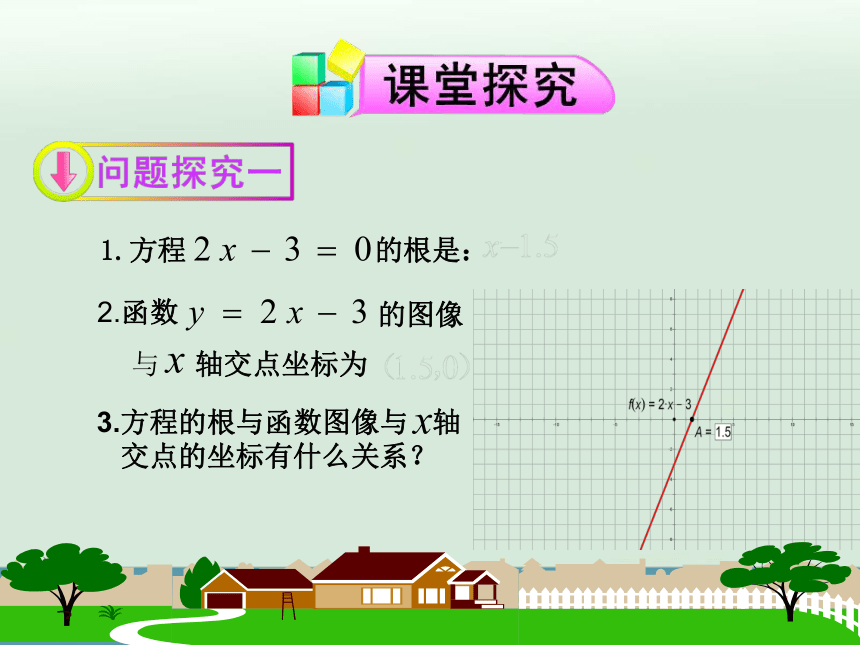
1.方程 的根是:
2.函数
的图像
与
轴交点坐标为
3.方程的根与函数图像与 轴
交点的坐标有什么关系?
函数的零点
:我们把函数y=f(x)的图像与横轴的交点的 横坐标称为这个函数的零点.
零点是实数而不是点
1.定义
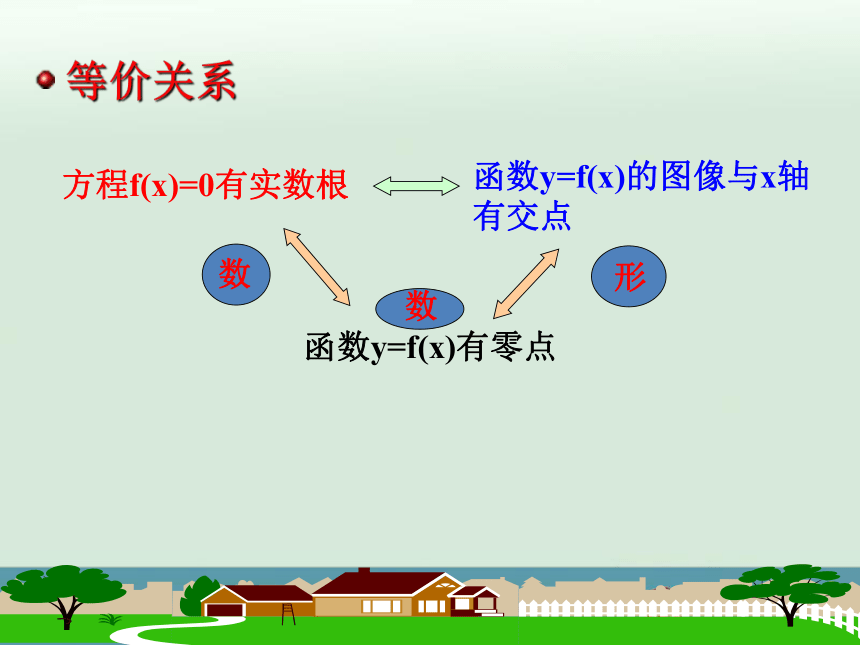
函数的零点
方程f(x)=0有实数根
函数y=f(x)有零点
等价关系
数
数
形
函数y=f(x)的图像与x轴有交点
函数y=f(x)在某个区间上是否一定有零点?
怎样的条件下,函数y=f(x)一定有零点?
1.函数
的零点是
2.由函数图像观察在其零点左右函数值得符号。
0
1
2
3
4
5
-1
-2
1
2
3
4
5
-1
-2
-3
-4
x
y
5
-3
-1
<
<
3
零点存在定理:
若函数y=f(x)在闭区间[a,b]上的图像是连续 曲线,并且在区间端点的函数值符号相反,即f(a)·f(b)<0,则在区间(a,b)内,函数y=f(x)至少有一个零点,即相应的方程f(x)=0在区间(a,b) 内至少有一个实数解.
思考:连续函数在区间(a,b)内有零点则
一定有 f(a)·f(b)<0吗?
x
y
0
a
b
.
.
(2)函数f(x)=–x3–3x+5的零点所在的大致区间为( )
A.(1,2) B.(–2,0) C.(0,1) D.(0,0.5 )
A
(1)判断函数 在区间[0,1]内是否有零点。
答:有零点
例3: 判断方程
是否有实数解,
如果有给出一个实数解的存在区间。
(0,2)
4.判断方程
是否有实根?并指出所在区间。
2.求证:函数
在区间[-2,-1]内存在零点,
3.判断方程
在区间[1,2]内有没有实数解?
并说明理由。
1.判断函数
在区间[2,3]内是否有零点。
方程
存在实数解吗?怎样判别?
思考题:
如果有请给出一个实数解的存在区间。
1.一个概念一组关系一个定理:
函数
方程
零点
根
数 值
存在性
个 数
2.两种思想:函数方程思想;数形结合思想.
3.函数零点存在性判别的三种方法:
(1)解方程
(2)画图像
(3)用定理判定
函数方程本一家,
数学王国它当家;
方程实根存在性,
函数符号来确定。
本节知识可以概括为:
第四章 函数应用
§1 函数与方程
1.理解函数零点的概念,领会函数零点与相应方程解的关系.(重点)
2.掌握零点存在的判定方法.(难点)
1.方程 的根是:
2.函数
的图像
与
轴交点坐标为
3.方程的根与函数图像与 轴
交点的坐标有什么关系?
函数的零点
:我们把函数y=f(x)的图像与横轴的交点的 横坐标称为这个函数的零点.
零点是实数而不是点
1.定义
函数的零点
方程f(x)=0有实数根
函数y=f(x)有零点
等价关系
数
数
形
函数y=f(x)的图像与x轴有交点
函数y=f(x)在某个区间上是否一定有零点?
怎样的条件下,函数y=f(x)一定有零点?
1.函数
的零点是
2.由函数图像观察在其零点左右函数值得符号。
0
1
2
3
4
5
-1
-2
1
2
3
4
5
-1
-2
-3
-4
x
y
5
-3
-1
<
<
3
零点存在定理:
若函数y=f(x)在闭区间[a,b]上的图像是连续 曲线,并且在区间端点的函数值符号相反,即f(a)·f(b)<0,则在区间(a,b)内,函数y=f(x)至少有一个零点,即相应的方程f(x)=0在区间(a,b) 内至少有一个实数解.
思考:连续函数在区间(a,b)内有零点则
一定有 f(a)·f(b)<0吗?
x
y
0
a
b
.
.
(2)函数f(x)=–x3–3x+5的零点所在的大致区间为( )
A.(1,2) B.(–2,0) C.(0,1) D.(0,0.5 )
A
(1)判断函数 在区间[0,1]内是否有零点。
答:有零点
例3: 判断方程
是否有实数解,
如果有给出一个实数解的存在区间。
(0,2)
4.判断方程
是否有实根?并指出所在区间。
2.求证:函数
在区间[-2,-1]内存在零点,
3.判断方程
在区间[1,2]内有没有实数解?
并说明理由。
1.判断函数
在区间[2,3]内是否有零点。
方程
存在实数解吗?怎样判别?
思考题:
如果有请给出一个实数解的存在区间。
1.一个概念一组关系一个定理:
函数
方程
零点
根
数 值
存在性
个 数
2.两种思想:函数方程思想;数形结合思想.
3.函数零点存在性判别的三种方法:
(1)解方程
(2)画图像
(3)用定理判定
函数方程本一家,
数学王国它当家;
方程实根存在性,
函数符号来确定。
本节知识可以概括为:
