北师大版高中数学必修一-4.1.1 方程的根与函数的零点 课件(27张PPT)
文档属性
| 名称 | 北师大版高中数学必修一-4.1.1 方程的根与函数的零点 课件(27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 561.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 00:00:00 | ||
图片预览







文档简介
方程的根与函数的零点
以下哪些是函数,哪些是方程?
求下列方程的根并
画出相应函数的简图
方程
函数
函
数
图
象
方程的根
图象与x轴交点
无实数根
无交点
x
y
x
y
一、基础知识讲解
O
x
y
O
O
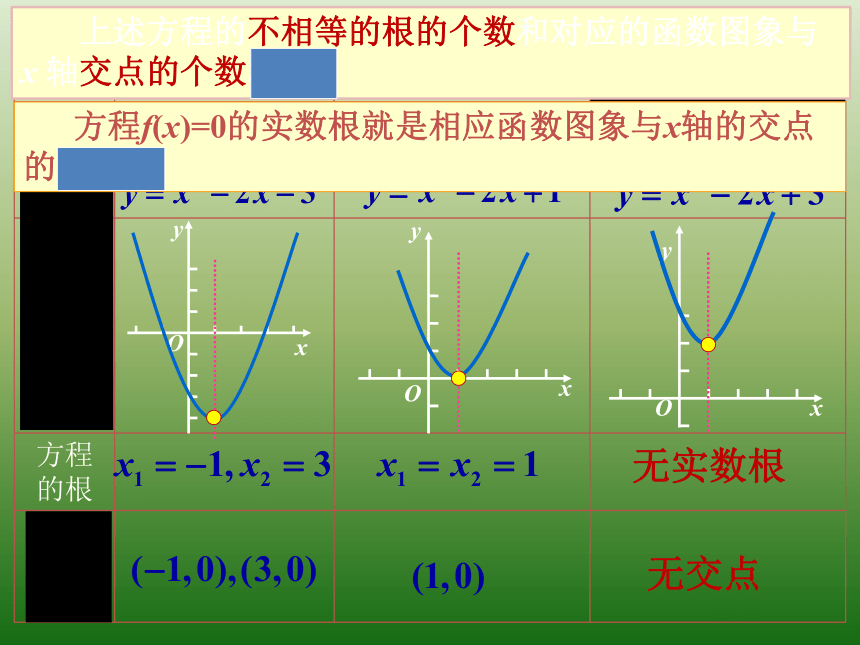
上述方程的不相等的根的个数和对应的函数图象与 x 轴交点的个数相同。
方程f(x)=0的实数根就是相应函数图象与x轴的交点的横坐标.
中外历史上的方程求解
《九章算术》给出了一次方程、二次方程和正系数三次方程的求根方法。
19世纪挪威数学家阿贝尔证明了五次及五次以上一般方程没有根式解。
11世纪,北宋数学家贾宪给出了三次及三次以上的方程的解法。
13世纪,南宋数学家秦九韶给出了求任意次代数方程的正根的解法
今天我们来学习方程的根与函数的零点!
2、有关函数与方程的三个等价关系:
函数 y=f(x) 的图象与 x 轴有交点
1、零点的定义:
对于函数 y=f(x) ,我们把使 f(x)=0 的 实数 x 叫做函数 y=f(x) 的零点。
函数 y=f(x) 有零点
一、基础知识讲解
思考:零点是不是一个点?
方程 f(x)=0 有实数根
由此可见:确定函数y=f(x)的零点的两种途径
(1)解方程 f(x)=0; (2)画图求与 x 轴的交点的横坐标
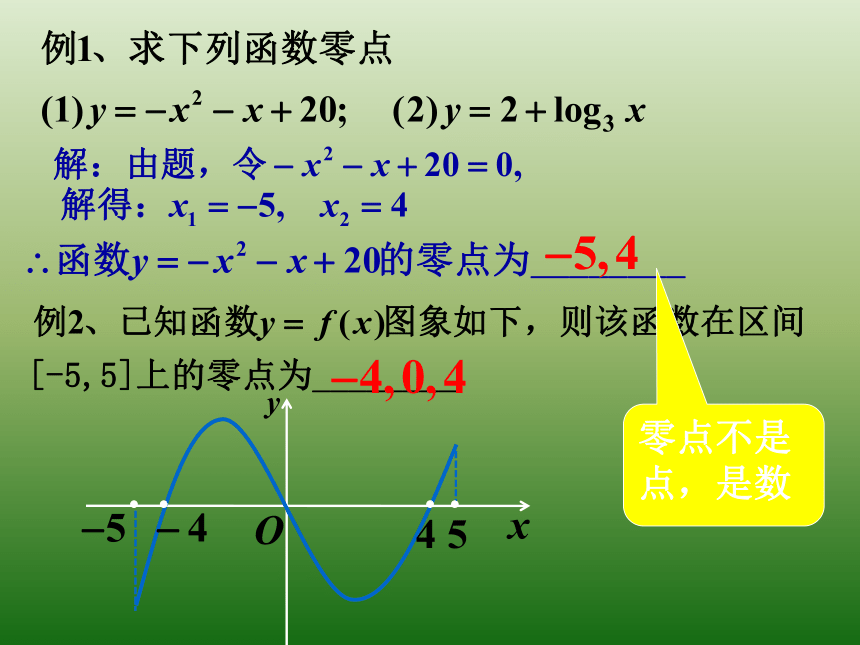
零点不是点,是实数
零点不是点,是数
三、基础知识讲解
函数
y = x2- 2x - 3
区间
(a,b)
有没零点
f(a)×f(b)的符号
(+或-)
结论
图象
(-2 , 0)
(0 , 2)
(2 , 4)
(4 , 5)
有
没有
有
没有
-
+
-
+
则函数在区间(a,b)
内有零点
f(a)×f(b) <0
连续不断
x
y
O
1 2 3
-2 -1
如果函数
的一条曲线,并且 f(a)·f(b)<0,
(a,b)内有零点,即存在
零点存在性定理:
连续不断
那么
c也就是方程
3 若 ,则函数在区间[a,b]内一定没有零点吗?
2 在定理的条件下,什么时候只有一个?
1 若满足了两个条件,则函数一定有零点,有几个?
思考:
4 若函数有零点,一定能找到一个区间[a,b],
使得 吗?
1 .不确定
2 .如果加入条件函数 在区间 [a,b] 上单调,则存在零点,且只有一个
3 .不一定
4 .不一定如
3.如果加入条件:函数在区间 上单调,则存在零点,且只有一个
注意:1.两个条件缺一不可
2.存在但不一定唯一
4.若 ,则函数零点可能存在,
也可能不存在
例2 判断正误,若不正确,请使用函数图象举出反例
(1)已知函数y=f(x)在区间[a,b]上连续,且f(a)·f(b)<0,则f(x)在区间(a,b)内有且仅有一个
零点.( )
(2)已知函数y=f(x)在区间[a,b]上连续,且f(a)·f(b)≥0,则f(x)在区间(a,b)内没有零点.( )
(3)已知函数y=f(x)在区间[a,b]上满足f(a)·f(b) <0,则f(x)在区间(a,b)内存在零点.( )
解:(1)已知函数y=f (x)在区间[a,b]上连续,且
f(a)·f(b)< 0,则f(x)在区间(a,b)内有且仅有一个
零点.
( )
a
b
O
x
y
如图,
函数y=f(x)在区间(a,b)上有3个零点,故“在区间(a,b) 内有且仅有一个零点”的说法是错误的.
(2)已知函数y=f(x)在区间[a,b]上连续,且f(a)·f(b) ≥0,则f(x)在区间(a,b)内没有零点.( )
a
b
O
x
y
可知,函数y=f(x)在区间[a,b]上连续,且f(a)·
f(b)≥0,但f(x)在区间(a,b)内有零点.故论断不正确。
如图,
三、基础知识讲解
A、
B、
C、
D、
四、例题分析
例1求函数 的零点的个数。
解法二:(画图象)
函数f(x)=lnx+2x-6的零点的个数就是方程lnx+2x-6=0(即lnx=6-2x)的根的个数,也就是函数y=lnx的图象和函数y=6-2x的图象交点的个数,
四、例题分析
五、基础知识讲解
1.函数f(x)=x2- 3x+2的零点是( )
A.(1,0) B.(2,0) C.(1,0) D.1,2
D
2.已知函数f(x)=x2+mx+n,若f(a)>0,f(b)>0,则函数f(x)
在区间(a,b)内( )
A.一定有零点 B.一定没有零点
C.可能有两个零点 D.至多有一个零点
C
六、针对性练习
4
求方程2-x =x的根的个数,并确定根所在的区间[n,n+1](n∈Z).
解:求方程 的根的个数,即求方程
的根的个数,即判断函数
与
的图象交点个数.由图可
知只有一个解.
y=x
1
O
x
1
2
3
4
y
【变式练习】
A.0 B.1 C.2 D.无数个
( )
C
B
( )
3.函数f(x)=x3+x-1在下列哪个区间内有零点( )
A.(-2,-1) B.(0,1)
C.(1,2) D.(2,3)
B
4.函数f(x)=2x+3x的零点所在的一个区间是( )
A.(-2,-1) B.(-1,0)
C.(0,1) D.(1,2)
【解析】∵f(x)=2x+3x,∴f(-1)=- <0,
f(0)=1>0.?
B
一个定义: 函数的零点
两个数学思想:函数与方程、数形结合的思想
三种方法:判断函数零点是否存的方法
小结提高
问题9:通过本节课的学习你学到了哪些数学知识?又学到了哪些重要的数学思想?
一个定理:零点存在定理
三个等价关系:
以下哪些是函数,哪些是方程?
求下列方程的根并
画出相应函数的简图
方程
函数
函
数
图
象
方程的根
图象与x轴交点
无实数根
无交点
x
y
x
y
一、基础知识讲解
O
x
y
O
O
上述方程的不相等的根的个数和对应的函数图象与 x 轴交点的个数相同。
方程f(x)=0的实数根就是相应函数图象与x轴的交点的横坐标.
中外历史上的方程求解
《九章算术》给出了一次方程、二次方程和正系数三次方程的求根方法。
19世纪挪威数学家阿贝尔证明了五次及五次以上一般方程没有根式解。
11世纪,北宋数学家贾宪给出了三次及三次以上的方程的解法。
13世纪,南宋数学家秦九韶给出了求任意次代数方程的正根的解法
今天我们来学习方程的根与函数的零点!
2、有关函数与方程的三个等价关系:
函数 y=f(x) 的图象与 x 轴有交点
1、零点的定义:
对于函数 y=f(x) ,我们把使 f(x)=0 的 实数 x 叫做函数 y=f(x) 的零点。
函数 y=f(x) 有零点
一、基础知识讲解
思考:零点是不是一个点?
方程 f(x)=0 有实数根
由此可见:确定函数y=f(x)的零点的两种途径
(1)解方程 f(x)=0; (2)画图求与 x 轴的交点的横坐标
零点不是点,是实数
零点不是点,是数
三、基础知识讲解
函数
y = x2- 2x - 3
区间
(a,b)
有没零点
f(a)×f(b)的符号
(+或-)
结论
图象
(-2 , 0)
(0 , 2)
(2 , 4)
(4 , 5)
有
没有
有
没有
-
+
-
+
则函数在区间(a,b)
内有零点
f(a)×f(b) <0
连续不断
x
y
O
1 2 3
-2 -1
如果函数
的一条曲线,并且 f(a)·f(b)<0,
(a,b)内有零点,即存在
零点存在性定理:
连续不断
那么
c也就是方程
3 若 ,则函数在区间[a,b]内一定没有零点吗?
2 在定理的条件下,什么时候只有一个?
1 若满足了两个条件,则函数一定有零点,有几个?
思考:
4 若函数有零点,一定能找到一个区间[a,b],
使得 吗?
1 .不确定
2 .如果加入条件函数 在区间 [a,b] 上单调,则存在零点,且只有一个
3 .不一定
4 .不一定如
3.如果加入条件:函数在区间 上单调,则存在零点,且只有一个
注意:1.两个条件缺一不可
2.存在但不一定唯一
4.若 ,则函数零点可能存在,
也可能不存在
例2 判断正误,若不正确,请使用函数图象举出反例
(1)已知函数y=f(x)在区间[a,b]上连续,且f(a)·f(b)<0,则f(x)在区间(a,b)内有且仅有一个
零点.( )
(2)已知函数y=f(x)在区间[a,b]上连续,且f(a)·f(b)≥0,则f(x)在区间(a,b)内没有零点.( )
(3)已知函数y=f(x)在区间[a,b]上满足f(a)·f(b) <0,则f(x)在区间(a,b)内存在零点.( )
解:(1)已知函数y=f (x)在区间[a,b]上连续,且
f(a)·f(b)< 0,则f(x)在区间(a,b)内有且仅有一个
零点.
( )
a
b
O
x
y
如图,
函数y=f(x)在区间(a,b)上有3个零点,故“在区间(a,b) 内有且仅有一个零点”的说法是错误的.
(2)已知函数y=f(x)在区间[a,b]上连续,且f(a)·f(b) ≥0,则f(x)在区间(a,b)内没有零点.( )
a
b
O
x
y
可知,函数y=f(x)在区间[a,b]上连续,且f(a)·
f(b)≥0,但f(x)在区间(a,b)内有零点.故论断不正确。
如图,
三、基础知识讲解
A、
B、
C、
D、
四、例题分析
例1求函数 的零点的个数。
解法二:(画图象)
函数f(x)=lnx+2x-6的零点的个数就是方程lnx+2x-6=0(即lnx=6-2x)的根的个数,也就是函数y=lnx的图象和函数y=6-2x的图象交点的个数,
四、例题分析
五、基础知识讲解
1.函数f(x)=x2- 3x+2的零点是( )
A.(1,0) B.(2,0) C.(1,0) D.1,2
D
2.已知函数f(x)=x2+mx+n,若f(a)>0,f(b)>0,则函数f(x)
在区间(a,b)内( )
A.一定有零点 B.一定没有零点
C.可能有两个零点 D.至多有一个零点
C
六、针对性练习
4
求方程2-x =x的根的个数,并确定根所在的区间[n,n+1](n∈Z).
解:求方程 的根的个数,即求方程
的根的个数,即判断函数
与
的图象交点个数.由图可
知只有一个解.
y=x
1
O
x
1
2
3
4
y
【变式练习】
A.0 B.1 C.2 D.无数个
( )
C
B
( )
3.函数f(x)=x3+x-1在下列哪个区间内有零点( )
A.(-2,-1) B.(0,1)
C.(1,2) D.(2,3)
B
4.函数f(x)=2x+3x的零点所在的一个区间是( )
A.(-2,-1) B.(-1,0)
C.(0,1) D.(1,2)
【解析】∵f(x)=2x+3x,∴f(-1)=- <0,
f(0)=1>0.?
B
一个定义: 函数的零点
两个数学思想:函数与方程、数形结合的思想
三种方法:判断函数零点是否存的方法
小结提高
问题9:通过本节课的学习你学到了哪些数学知识?又学到了哪些重要的数学思想?
一个定理:零点存在定理
三个等价关系:
