北师大版高中数学必修一-4.1.1 利用函数性质判定方程解的存在 课件 (1)13张PPT
文档属性
| 名称 | 北师大版高中数学必修一-4.1.1 利用函数性质判定方程解的存在 课件 (1)13张PPT |  | |
| 格式 | pptx | ||
| 文件大小 | 598.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 10:52:55 | ||
图片预览


文档简介
1.1利用函数性质判定方程解的存在
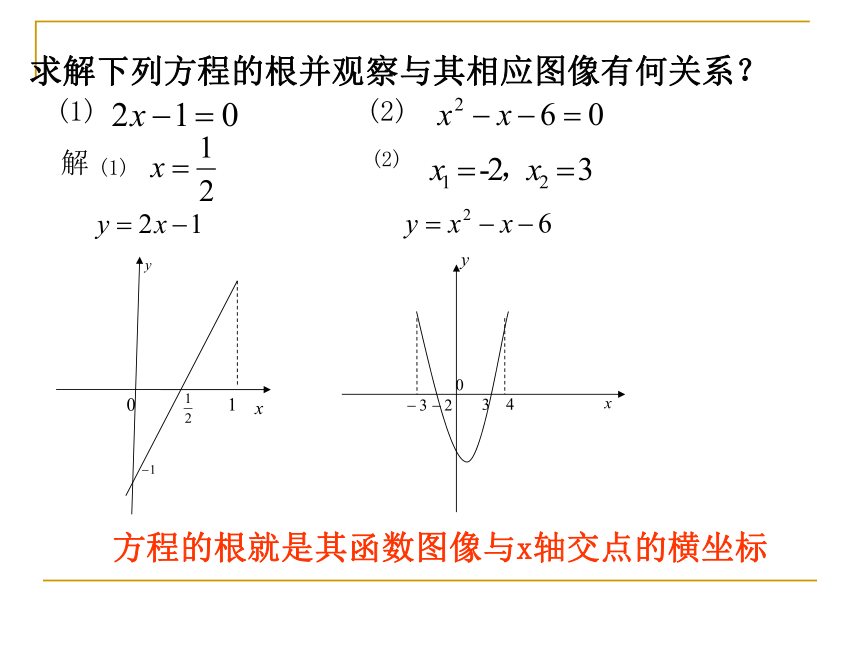
求解下列方程的根并观察与其相应图像有何关系?
(1)
(2)
解
(1)
(2)
方程的根就是其函数图像与x轴交点的横坐标
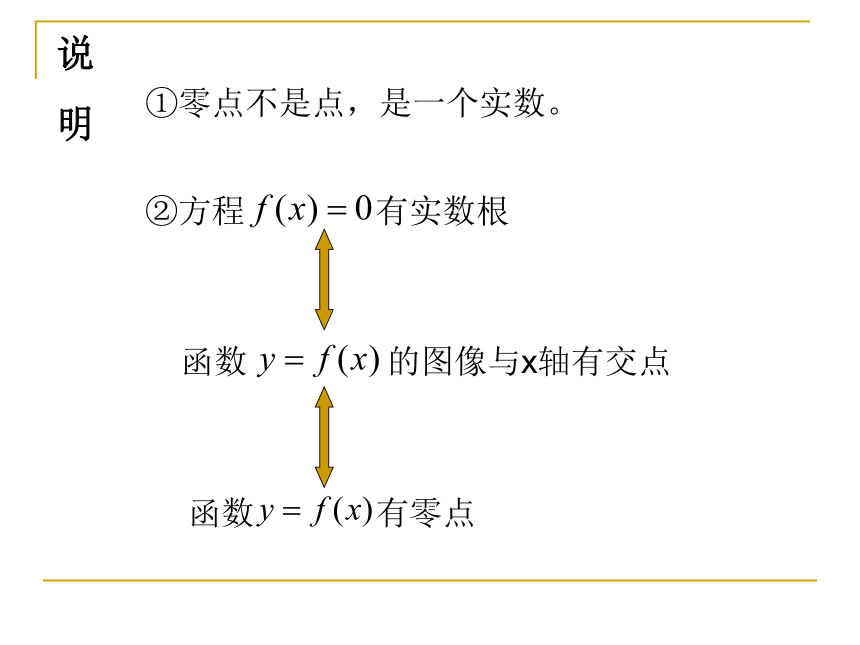
①零点不是点,是一个实数。
②方程 有实数根
函数 的图像与x轴有交点
函数 有零点
说 明
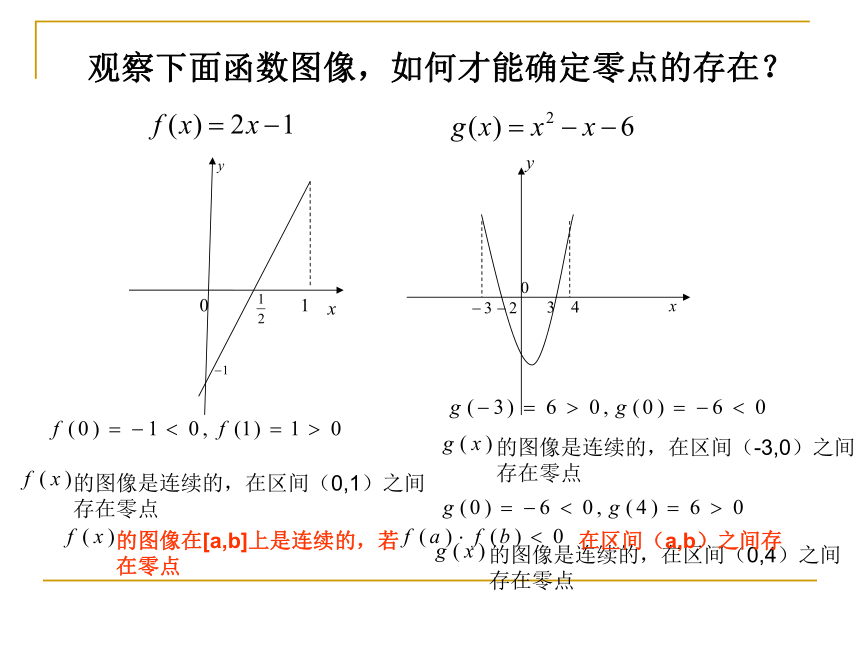
观察下面函数图像,如何才能确定零点的存在?
的图像是连续的,在区间(0,1)之间存在零点
的图像是连续的,在区间(-3,0)之间存在零点
的图像是连续的,在区间(0,4)之间存在零点
的图像在[a,b]上是连续的,若 在区间(a,b)之间存在零点
说 明
①图像连续。
但没有零点
②区间的“闭”与“开”.“闭”是为了保证 , 值的存在性,“开”是为了强调零点在区间的内部.
③该定理只是指出了方程解的存在性,不能确定解的个数
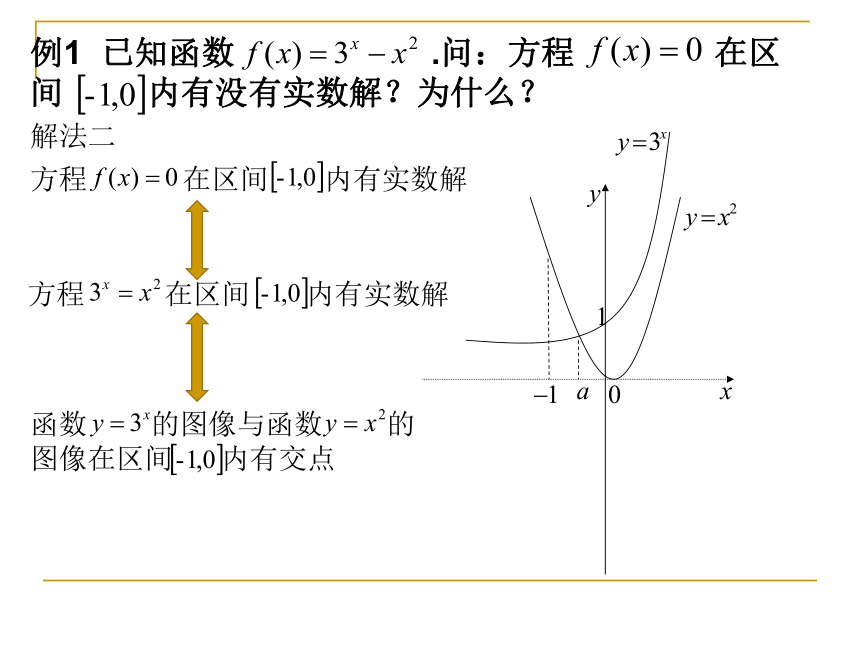
例1 已知函数 .问:方程 在区间 内有没有实数解?为什么?
解法二
方程 在区间 内有实数解
方程 在区间 内有实数解
函数 的图像与函数 的图像在区间 内有交点
变式:
若 .问:方程 在区间 内有
没有实数解?
分析: , 不符合定理条件,但我们发现该方程在区间 内是有解的.
所以满足定理条件,则函数 在区间
必有零点,若不满足条件也可能存在零点
例2 判定方程 有两个相异的实数解,且一个大于5,一个小于2.
解
因为 的图像是开口向上的抛物线,
所以在 内存在一点a, ,
在 内存在一点 b, .所以
抛物线与横轴在 内有一个交点,
在 内也有一个交点.所以
方程 有两个相异的实数解,
且一个大于5,一个小于2.
函数图像连续,所以在区间(1,2)内存在零点
函数图像连续,所以在区间(5,6)内存在零点
1
-
练习巩固
2、指出下列方程存在实数解,并给出一个实数解的存在区间:
选择
若函数 在区间 上单调且 则在区间 内,函数 ______零点.
A.至少一个 B.至多一个 C.只有一个 D.不能确定
0
B
所以满足定理条件,则函数 在区间
必有零点,若不满足条件也可能存在零点
课堂小结
1、零点的概念,零点存在判定定理以及应用
2、函数与方程、数形结合思想
作 业
预习下一节课
谢谢大家!
求解下列方程的根并观察与其相应图像有何关系?
(1)
(2)
解
(1)
(2)
方程的根就是其函数图像与x轴交点的横坐标
①零点不是点,是一个实数。
②方程 有实数根
函数 的图像与x轴有交点
函数 有零点
说 明
观察下面函数图像,如何才能确定零点的存在?
的图像是连续的,在区间(0,1)之间存在零点
的图像是连续的,在区间(-3,0)之间存在零点
的图像是连续的,在区间(0,4)之间存在零点
的图像在[a,b]上是连续的,若 在区间(a,b)之间存在零点
说 明
①图像连续。
但没有零点
②区间的“闭”与“开”.“闭”是为了保证 , 值的存在性,“开”是为了强调零点在区间的内部.
③该定理只是指出了方程解的存在性,不能确定解的个数
例1 已知函数 .问:方程 在区间 内有没有实数解?为什么?
解法二
方程 在区间 内有实数解
方程 在区间 内有实数解
函数 的图像与函数 的图像在区间 内有交点
变式:
若 .问:方程 在区间 内有
没有实数解?
分析: , 不符合定理条件,但我们发现该方程在区间 内是有解的.
所以满足定理条件,则函数 在区间
必有零点,若不满足条件也可能存在零点
例2 判定方程 有两个相异的实数解,且一个大于5,一个小于2.
解
因为 的图像是开口向上的抛物线,
所以在 内存在一点a, ,
在 内存在一点 b, .所以
抛物线与横轴在 内有一个交点,
在 内也有一个交点.所以
方程 有两个相异的实数解,
且一个大于5,一个小于2.
函数图像连续,所以在区间(1,2)内存在零点
函数图像连续,所以在区间(5,6)内存在零点
1
-
练习巩固
2、指出下列方程存在实数解,并给出一个实数解的存在区间:
选择
若函数 在区间 上单调且 则在区间 内,函数 ______零点.
A.至少一个 B.至多一个 C.只有一个 D.不能确定
0
B
所以满足定理条件,则函数 在区间
必有零点,若不满足条件也可能存在零点
课堂小结
1、零点的概念,零点存在判定定理以及应用
2、函数与方程、数形结合思想
作 业
预习下一节课
谢谢大家!
