北师大版高中数学必修一-4.1.1 利用函数性质判定方程解的存在 课件 (3)(12张PPT)
文档属性
| 名称 | 北师大版高中数学必修一-4.1.1 利用函数性质判定方程解的存在 课件 (3)(12张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 118.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 10:56:24 | ||
图片预览



文档简介
4.1.1利用函数性质判定方程解的存在
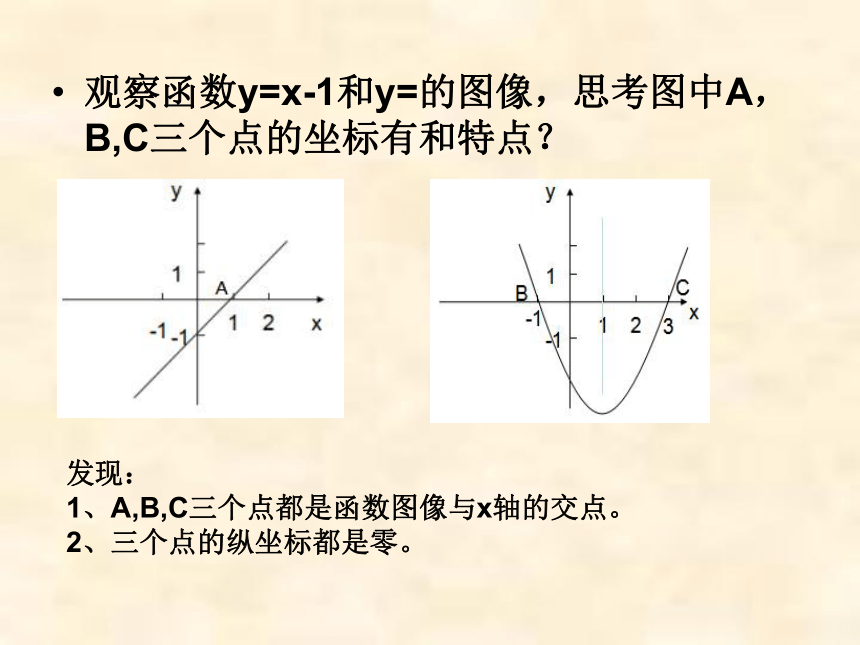
观察函数y=x-1和y=的图像,思考图中A,B,C三个点的坐标有和特点?
发现:
1、A,B,C三个点都是函数图像与x轴的交点。
2、三个点的纵坐标都是零。
函数零点定义:
我们把函数y=f(x)的图像与横轴交点的横坐标称为这个函数的零点。
拓展:函数y=f(x)的零点可以理解成方程
f(x)=0的解。
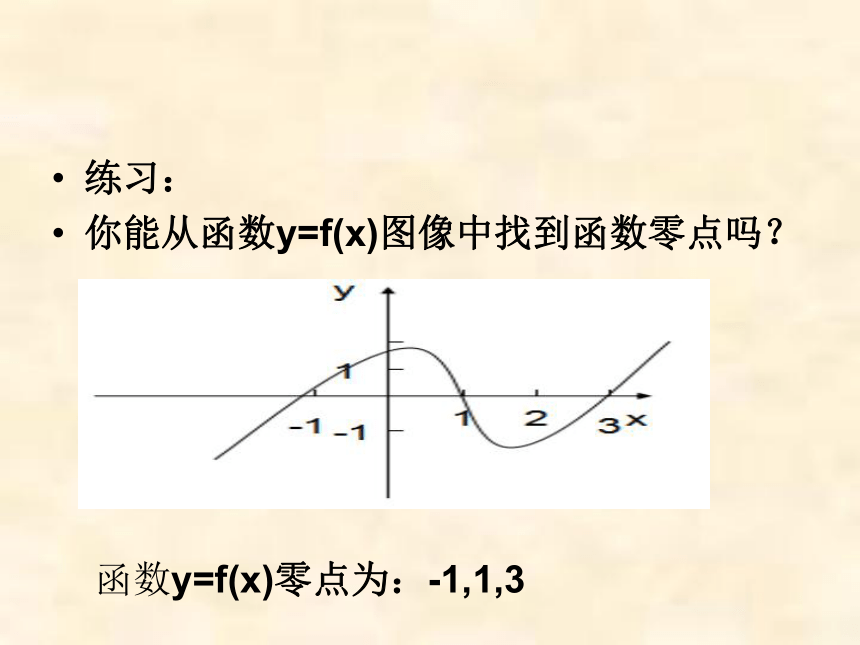
练习:
你能从函数y=f(x)图像中找到函数零点吗?
函数y=f(x)零点为:-1,1,3
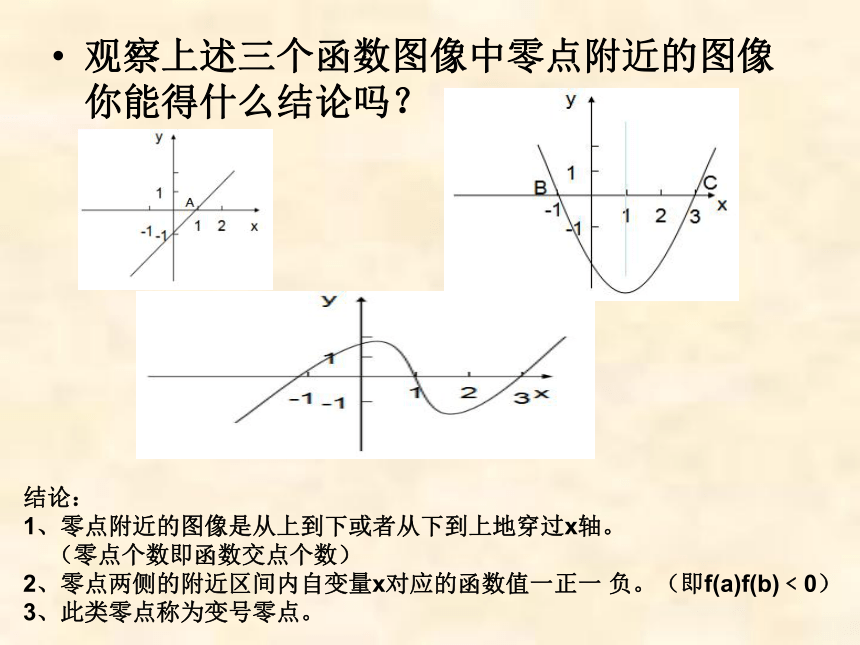
观察上述三个函数图像中零点附近的图像你能得什么结论吗?
结论:
1、零点附近的图像是从上到下或者从下到上地穿过x轴。
(零点个数即函数交点个数)
2、零点两侧的附近区间内自变量x对应的函数值一正一 负。(即f(a)f(b)﹤0)
3、此类零点称为变号零点。
练习
作出 函数图像确定函数有没有零点?能否用上述结论中f(a)f(b)﹤0来判断函数有零点?
结论:
函数没有零点,用f(a)f(b)﹤0判断零点必须是连续区间[a,b]上函数图像是连续的。
(1)几何法:函数y=f(x)图像与x轴交点横坐标,即有几个交点就有几个零点。
(2)代数法:
?函数y=f(x)图像在[a,b]上是连续的。
?满足f(a)f(b)﹤0
?函数f(x)在区间(a,b)上至少一个零点。
结论:零点的判断方法
思考:
如何判定函数f(x)在区间(a,b)上有唯一零点?
解决办法:
在原有判断方法的基础上:加入区间(a,b)上的单调性即可。
例1:判定方程3x-x2=0在(-1,0)上是
否有解。
例2:判定方程x3+2x+1=0在区间(-2,3)上是
否有解?
例3 判断方程 是否有解。
画出函数f(x)= 的图像如下:
y
x
0
1
Y=
从图可得:方程 有两个解,即为图中交点
的横坐标。
方法一:
题中方程可变形为
则可得到两个函数y= 及y=
可画出两个函数图象如下:
Y=
Y=
x
y
0
1
从图可得:方程 在(0,1)和(1,+∞)上各有一解。
①函数图象与x轴交点的横坐标叫做函数的零点,即
函数的零点为对应方程的解。
②利用函数图像判断方程的解更加直观。
③数形结合思想的应用。
④发散思维一题多解。
方法二:
小结:
课堂练习:
1、判断方程x3-x=0在[-2,2]上是否有解。
2、判断方程x3+x=0 在(-∞,0)上是否
有解。
3、利用函数增长的快慢判断方程x3=2x是
否有解。
观察函数y=x-1和y=的图像,思考图中A,B,C三个点的坐标有和特点?
发现:
1、A,B,C三个点都是函数图像与x轴的交点。
2、三个点的纵坐标都是零。
函数零点定义:
我们把函数y=f(x)的图像与横轴交点的横坐标称为这个函数的零点。
拓展:函数y=f(x)的零点可以理解成方程
f(x)=0的解。
练习:
你能从函数y=f(x)图像中找到函数零点吗?
函数y=f(x)零点为:-1,1,3
观察上述三个函数图像中零点附近的图像你能得什么结论吗?
结论:
1、零点附近的图像是从上到下或者从下到上地穿过x轴。
(零点个数即函数交点个数)
2、零点两侧的附近区间内自变量x对应的函数值一正一 负。(即f(a)f(b)﹤0)
3、此类零点称为变号零点。
练习
作出 函数图像确定函数有没有零点?能否用上述结论中f(a)f(b)﹤0来判断函数有零点?
结论:
函数没有零点,用f(a)f(b)﹤0判断零点必须是连续区间[a,b]上函数图像是连续的。
(1)几何法:函数y=f(x)图像与x轴交点横坐标,即有几个交点就有几个零点。
(2)代数法:
?函数y=f(x)图像在[a,b]上是连续的。
?满足f(a)f(b)﹤0
?函数f(x)在区间(a,b)上至少一个零点。
结论:零点的判断方法
思考:
如何判定函数f(x)在区间(a,b)上有唯一零点?
解决办法:
在原有判断方法的基础上:加入区间(a,b)上的单调性即可。
例1:判定方程3x-x2=0在(-1,0)上是
否有解。
例2:判定方程x3+2x+1=0在区间(-2,3)上是
否有解?
例3 判断方程 是否有解。
画出函数f(x)= 的图像如下:
y
x
0
1
Y=
从图可得:方程 有两个解,即为图中交点
的横坐标。
方法一:
题中方程可变形为
则可得到两个函数y= 及y=
可画出两个函数图象如下:
Y=
Y=
x
y
0
1
从图可得:方程 在(0,1)和(1,+∞)上各有一解。
①函数图象与x轴交点的横坐标叫做函数的零点,即
函数的零点为对应方程的解。
②利用函数图像判断方程的解更加直观。
③数形结合思想的应用。
④发散思维一题多解。
方法二:
小结:
课堂练习:
1、判断方程x3-x=0在[-2,2]上是否有解。
2、判断方程x3+x=0 在(-∞,0)上是否
有解。
3、利用函数增长的快慢判断方程x3=2x是
否有解。
