北师大版高中数学必修一-4.1.1 利用函数性质判定方程解的存在 课件 (4)(11张PPT)
文档属性
| 名称 | 北师大版高中数学必修一-4.1.1 利用函数性质判定方程解的存在 课件 (4)(11张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 236.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 00:00:00 | ||
图片预览




文档简介
第四章 函数应用
§ 1.1利用函数性质判断方程解的存在
本节课需要解决的问题:
1、给定一个方程如何判断它有无根
2、若有根能否确定根所在的范围
观察与思考
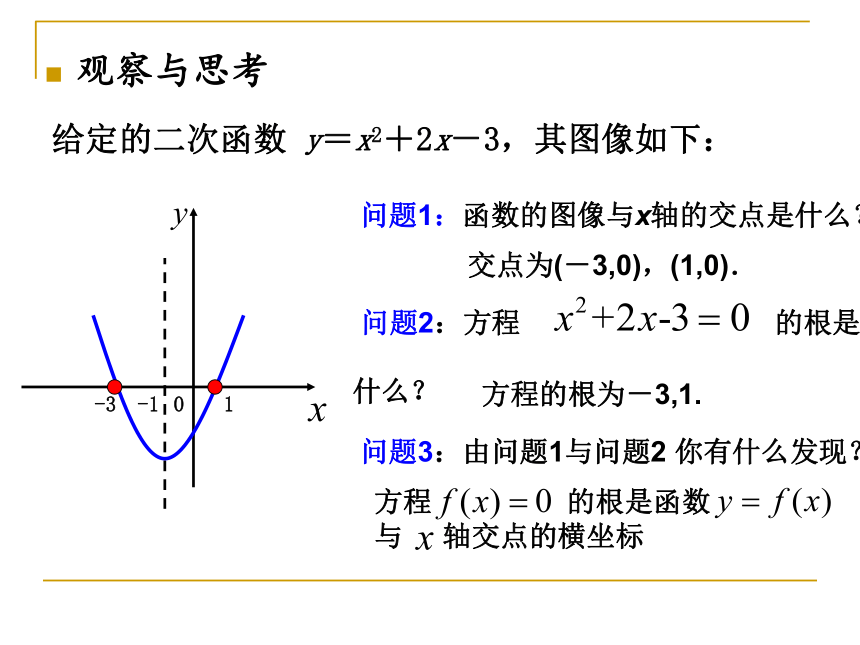
1
-1
-3
给定的二次函数 y=x2+2x-3,其图像如下:
问题2:方程 的根是什么?
方程的根为-3,1.
交点为(-3,0),(1,0).
问题3:由问题1与问题2 你有什么发现?
问题1:函数的图像与x轴的交点是什么?
方程 的根是函数 与 轴交点的横坐标
0
函数的零点
我们把函数 的图像与横轴的 交点的横坐标 称为这个函数的零点.
方程 有实数解
函数 的图像与 轴有交点
函数 零点
几个等价关系:
知识探究
函数零点存在性的判断
观察二次函数 的图像:
x
y
-2
1
2
-1
-2
-3
-4
知识探究
函数 在区间 内有一零点
函数 在区间 内有一零点
-1
0
1
2
3
4
零点存在定理:
若函数 在区间 上的图像是 ,
并且在区间端点的函数值符号相反,即 ,则在区间 内,函数 至少有一个零点,即相应的方程 在区间 内
知识探究
连 续曲线
连 续曲线
至少有一个实数解.
至少有一个实数解.
x
y
-2
1
2
-1
-2
-3
-4
-1
0
1
2
3
4
注:
(1)此定理的两个条件
① 函数在闭区间上的图像是连续曲线
缺一不可
(2) 此定理只能判断出零点的存在性,而不能判断出零点的个数
②
一、判断零点所在的区间
[例1] 已知函数 .问:方程 在区间 内有没有实数解?为什么?
因为
函数 图像是连续曲线,
所以 在区间 内有零点,
即在区间 内有实数解
实 践 应 用
解
练习1
函数 的零点所在的大致区间是 ( )
解析:
在区间 上有零点
巩 固 提 升
D
[例2] 求函数 零点的个数.
解:
由零点存在性定理知 在区间 上必定存在零点
又易知 在定义域内单调递增
故方程 有且只有一个实数解
即函数 仅有一个零点
实 践 应 用
二、判断函数零点的个数
课堂小结
(1)方程的根与相应函数的关系
(2)函数零点存在性的判断——零点存在定理
作 业
习题4-1 A组 1 , 2 , 4
§ 1.1利用函数性质判断方程解的存在
本节课需要解决的问题:
1、给定一个方程如何判断它有无根
2、若有根能否确定根所在的范围
观察与思考
1
-1
-3
给定的二次函数 y=x2+2x-3,其图像如下:
问题2:方程 的根是什么?
方程的根为-3,1.
交点为(-3,0),(1,0).
问题3:由问题1与问题2 你有什么发现?
问题1:函数的图像与x轴的交点是什么?
方程 的根是函数 与 轴交点的横坐标
0
函数的零点
我们把函数 的图像与横轴的 交点的横坐标 称为这个函数的零点.
方程 有实数解
函数 的图像与 轴有交点
函数 零点
几个等价关系:
知识探究
函数零点存在性的判断
观察二次函数 的图像:
x
y
-2
1
2
-1
-2
-3
-4
知识探究
函数 在区间 内有一零点
函数 在区间 内有一零点
-1
0
1
2
3
4
零点存在定理:
若函数 在区间 上的图像是 ,
并且在区间端点的函数值符号相反,即 ,则在区间 内,函数 至少有一个零点,即相应的方程 在区间 内
知识探究
连 续曲线
连 续曲线
至少有一个实数解.
至少有一个实数解.
x
y
-2
1
2
-1
-2
-3
-4
-1
0
1
2
3
4
注:
(1)此定理的两个条件
① 函数在闭区间上的图像是连续曲线
缺一不可
(2) 此定理只能判断出零点的存在性,而不能判断出零点的个数
②
一、判断零点所在的区间
[例1] 已知函数 .问:方程 在区间 内有没有实数解?为什么?
因为
函数 图像是连续曲线,
所以 在区间 内有零点,
即在区间 内有实数解
实 践 应 用
解
练习1
函数 的零点所在的大致区间是 ( )
解析:
在区间 上有零点
巩 固 提 升
D
[例2] 求函数 零点的个数.
解:
由零点存在性定理知 在区间 上必定存在零点
又易知 在定义域内单调递增
故方程 有且只有一个实数解
即函数 仅有一个零点
实 践 应 用
二、判断函数零点的个数
课堂小结
(1)方程的根与相应函数的关系
(2)函数零点存在性的判断——零点存在定理
作 业
习题4-1 A组 1 , 2 , 4
