北师大版高中数学必修一-4.1.1 利用函数性质判定方程解的存在 课件 (2)(13张PPT)
文档属性
| 名称 | 北师大版高中数学必修一-4.1.1 利用函数性质判定方程解的存在 课件 (2)(13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 00:00:00 | ||
图片预览






文档简介
利用函数性质判定方程解的存在
从不同的角度看问题
一次函数
二元一次方程
一条直线
令
即
方程
的根
函数
的图象与
轴的交点的横坐标
函数
的零点
——数的角度
——形的角度
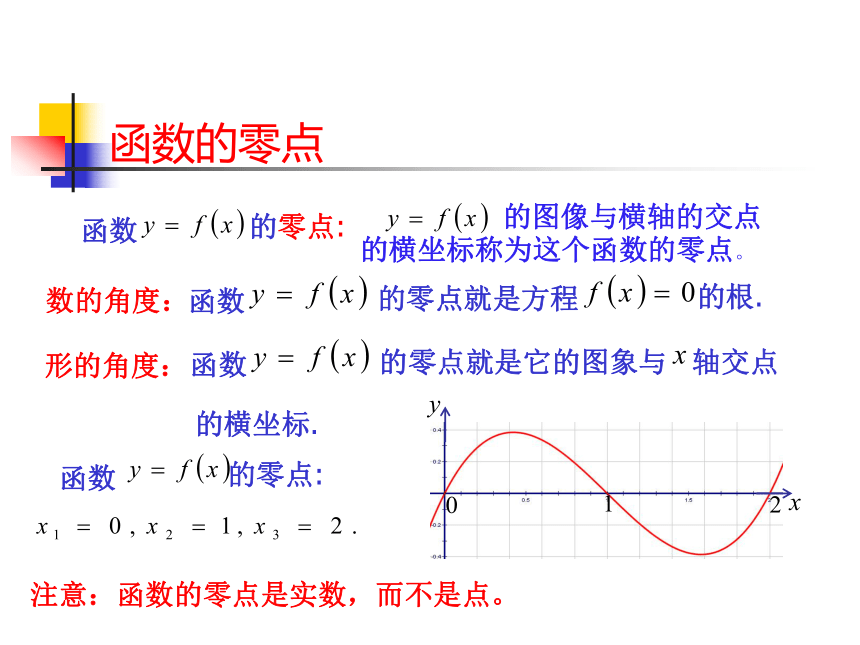
函数的零点
函数
的零点:
函数
的零点就是方程
的根.
数的角度:
形的角度:
函数
的零点就是它的图象与 轴交点
的横坐标.
函数
的零点:
的图像与横轴的交点的横坐标称为这个函数的零点。
注意:函数的零点是实数,而不是点。
几个等价关系:
方程 有实数根?函数 的图象与x轴有交点?函数 有零点,而且方程 的实数根个数等于函数
的零点个数。
问题1.是否任意函数都有零点?
提示:并非任意函数都有零点,只有 有根的函数 才有零点.
判断下列函数是否存在零点,如果存在,请求出。
求函数零点的两种方法(1)代数法:求方程 的实数根;
(2)几何法:对于不能用求根公式的方程,可以将它与函数
的图像联系起来,并利用函数的性质找出零点。
二次函数的零点
例1:确定二次函数
的零点个数.
数的角度:
形的角度:
方程
的根的个数.
函数
的图象与 轴
交点的个数.
变1:确定二次函数
的零点个数.
变2:确定二次函数
的零点个数.
x
y
0
——△>0
——△=0
——△<0
2.二次函数y=ax2+bx+c(a>0)的图象与零点的关系
Δ>0
Δ=0
Δ<0
二次函数y=ax2+bx+c (a>0)的图象
与x轴的交点
______,________
(x1,0)或
(x2,0)
无交点
零点个数
两个
一个
零个
(x1,0)
(x2,0)
变3:判断二次函数
在区间
上是否存在零点.
数的角度—
求根法
形的角度—
变式探究
你会用符号语言来刻画这一图形特征吗?
,图象不间断
函数
在区间
上存在零点.
一般化
图象不间断
图象不间断
图象不间断,
函数
在区间
上存在零点.
函数
在区间
上存在零点.
若函数
上的图象是一条连续曲线,
在区间
并且在区间端点的函数值符号相反,即
则在区间 内,函数 至少有一个零点,即方程 在区间 至少有一个实数解。
零点存在性定理
问题2:为什么是开区间 内有零点,而不是闭区间 上有零点?
提示:在上面的条件下, 内的零点至少有一个,还可能有其他零点,个数不确定。
问题3:在上面的条件下, 内的零点有几个?
如果函数 y=f(x) 在 上,图象是连续的,并且在闭区间的两个端点上的函数值互异即 ,且是单调函数,那么这个函数在 内必有唯一的一个零点。
函数f(x)=2x+3x的零点所在的一个区间是( )
A.(-2,-1) B.(-1,0)
C.(0,1) D.(1,2)
小试牛刀
例2:求证:函数
在区间
上存在零点.
证:
且函数
的图象在区间
上的图象是不间断的,
故函数
在区间
上存在零点.
【规律小结】 判定函数零点个数的几种方法:
(1)直接做出函数图象,看它和x轴有几个交点就有几个零点。
(2)直接求零点:令f(x)=0,如果能求出解,则有几个解就有几个零点;
(3)利用图象交点的个数:画出两个函数的图象,看其交点的个数,其中交点的横坐标有几个不同的值,就有几个不同的零点
(4)零点存在性定理:利用定理不仅要求函数在区间[a,b]上是连续不断的曲线,且f(a)·f(b)<0,还必须结合函数的图象与性质(如单调性、奇偶性)才能确定函数有多少个零点;
请各位老师批评指正
谢谢!
从不同的角度看问题
一次函数
二元一次方程
一条直线
令
即
方程
的根
函数
的图象与
轴的交点的横坐标
函数
的零点
——数的角度
——形的角度
函数的零点
函数
的零点:
函数
的零点就是方程
的根.
数的角度:
形的角度:
函数
的零点就是它的图象与 轴交点
的横坐标.
函数
的零点:
的图像与横轴的交点的横坐标称为这个函数的零点。
注意:函数的零点是实数,而不是点。
几个等价关系:
方程 有实数根?函数 的图象与x轴有交点?函数 有零点,而且方程 的实数根个数等于函数
的零点个数。
问题1.是否任意函数都有零点?
提示:并非任意函数都有零点,只有 有根的函数 才有零点.
判断下列函数是否存在零点,如果存在,请求出。
求函数零点的两种方法(1)代数法:求方程 的实数根;
(2)几何法:对于不能用求根公式的方程,可以将它与函数
的图像联系起来,并利用函数的性质找出零点。
二次函数的零点
例1:确定二次函数
的零点个数.
数的角度:
形的角度:
方程
的根的个数.
函数
的图象与 轴
交点的个数.
变1:确定二次函数
的零点个数.
变2:确定二次函数
的零点个数.
x
y
0
——△>0
——△=0
——△<0
2.二次函数y=ax2+bx+c(a>0)的图象与零点的关系
Δ>0
Δ=0
Δ<0
二次函数y=ax2+bx+c (a>0)的图象
与x轴的交点
______,________
(x1,0)或
(x2,0)
无交点
零点个数
两个
一个
零个
(x1,0)
(x2,0)
变3:判断二次函数
在区间
上是否存在零点.
数的角度—
求根法
形的角度—
变式探究
你会用符号语言来刻画这一图形特征吗?
,图象不间断
函数
在区间
上存在零点.
一般化
图象不间断
图象不间断
图象不间断,
函数
在区间
上存在零点.
函数
在区间
上存在零点.
若函数
上的图象是一条连续曲线,
在区间
并且在区间端点的函数值符号相反,即
则在区间 内,函数 至少有一个零点,即方程 在区间 至少有一个实数解。
零点存在性定理
问题2:为什么是开区间 内有零点,而不是闭区间 上有零点?
提示:在上面的条件下, 内的零点至少有一个,还可能有其他零点,个数不确定。
问题3:在上面的条件下, 内的零点有几个?
如果函数 y=f(x) 在 上,图象是连续的,并且在闭区间的两个端点上的函数值互异即 ,且是单调函数,那么这个函数在 内必有唯一的一个零点。
函数f(x)=2x+3x的零点所在的一个区间是( )
A.(-2,-1) B.(-1,0)
C.(0,1) D.(1,2)
小试牛刀
例2:求证:函数
在区间
上存在零点.
证:
且函数
的图象在区间
上的图象是不间断的,
故函数
在区间
上存在零点.
【规律小结】 判定函数零点个数的几种方法:
(1)直接做出函数图象,看它和x轴有几个交点就有几个零点。
(2)直接求零点:令f(x)=0,如果能求出解,则有几个解就有几个零点;
(3)利用图象交点的个数:画出两个函数的图象,看其交点的个数,其中交点的横坐标有几个不同的值,就有几个不同的零点
(4)零点存在性定理:利用定理不仅要求函数在区间[a,b]上是连续不断的曲线,且f(a)·f(b)<0,还必须结合函数的图象与性质(如单调性、奇偶性)才能确定函数有多少个零点;
请各位老师批评指正
谢谢!
