高中数学沪教版(上海)15章15.1 多面体的概念课件(20张PPT)
文档属性
| 名称 | 高中数学沪教版(上海)15章15.1 多面体的概念课件(20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 413.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 00:00:00 | ||
图片预览


文档简介
多面体的概念
多面体概念
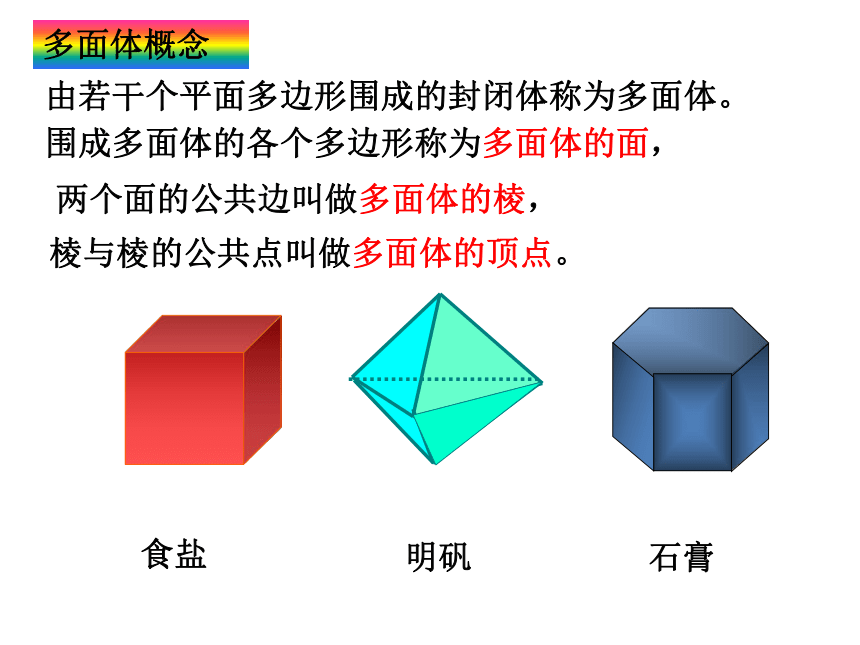
由若干个平面多边形围成的封闭体称为多面体。
围成多面体的各个多边形称为多面体的面,
食盐
明矾
石膏
两个面的公共边叫做多面体的棱,
棱与棱的公共点叫做多面体的顶点。
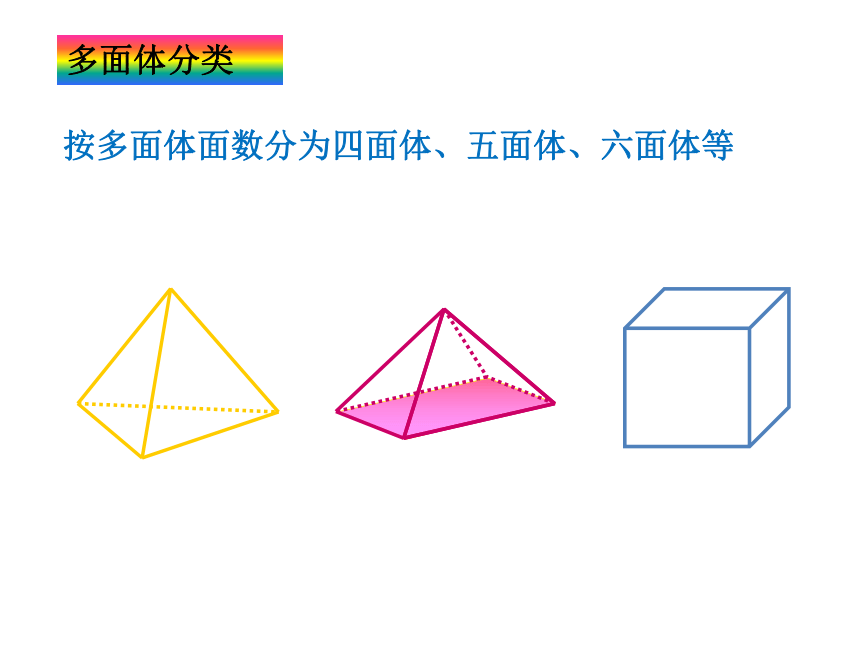
多面体分类
按多面体面数分为四面体、五面体、六面体等
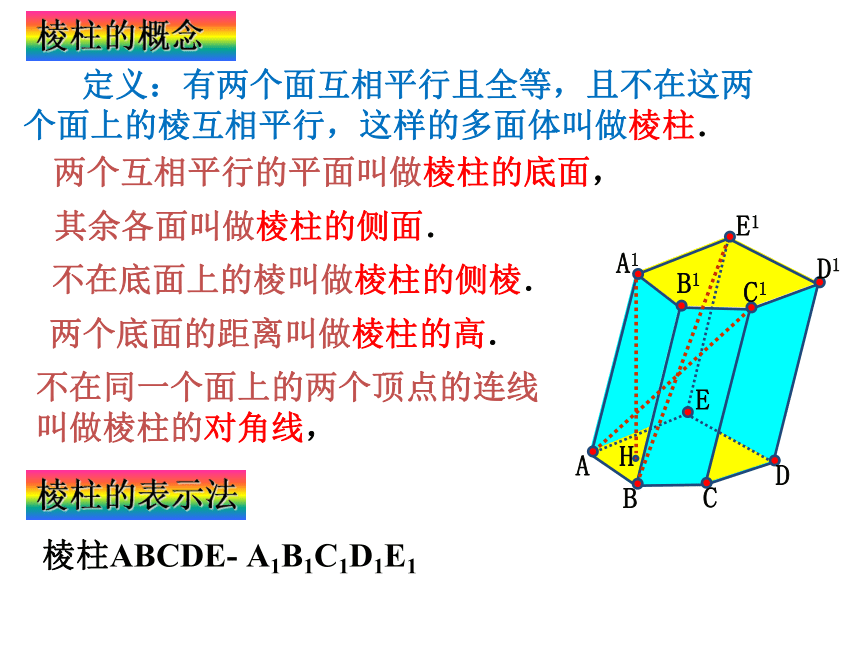
定义:有两个面互相平行且全等,且不在这两个面上的棱互相平行,这样的多面体叫做棱柱.
不在底面上的棱叫做棱柱的侧棱.
两个互相平行的平面叫做棱柱的底面,
棱柱的概念
A
B
C
D
D1
E1
A1
B1
C1
E
H
其余各面叫做棱柱的侧面.
两个底面的距离叫做棱柱的高.
不在同一个面上的两个顶点的连线
叫做棱柱的对角线,
棱柱的表示法
棱柱ABCDE- A1B1C1D1E1
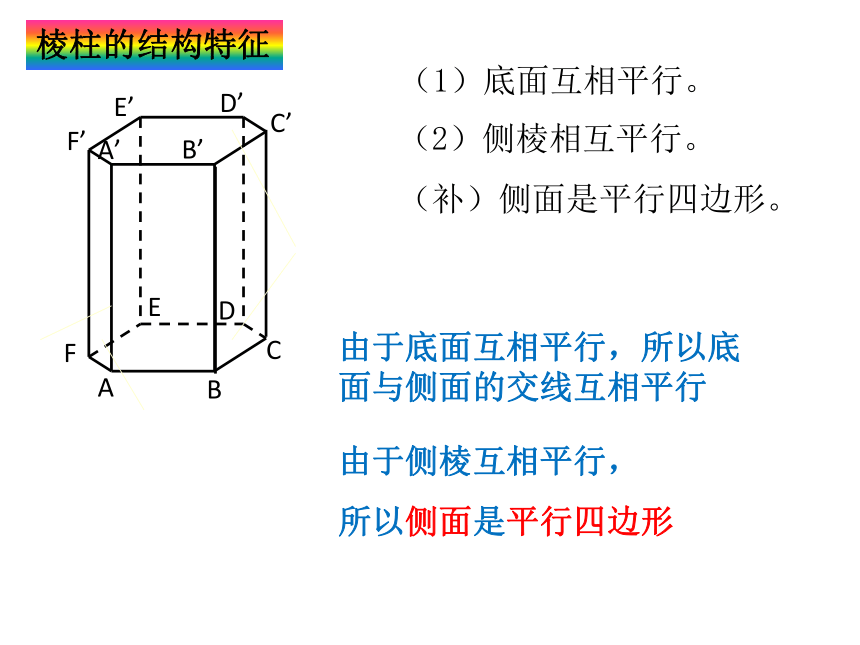
棱柱的结构特征
D
A
B
C
E
F
F’
A’
E’
D’
B’
C’
(1)底面互相平行。
(补)侧面是平行四边形。
(2)侧棱相互平行。
由于底面互相平行,所以底面与侧面的交线互相平行
由于侧棱互相平行,
所以侧面是平行四边形
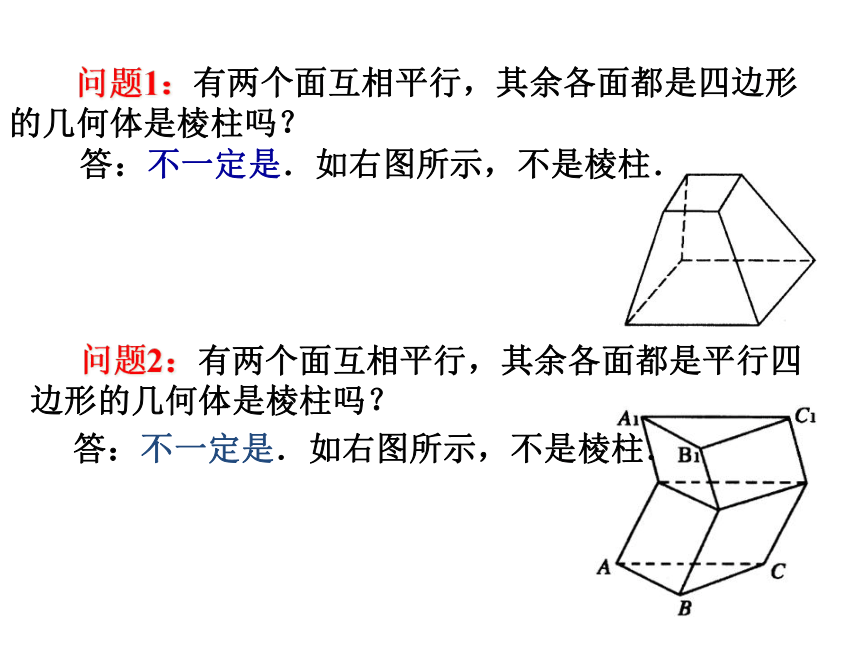
问题1:有两个面互相平行,其余各面都是四边形的几何体是棱柱吗?
答:不一定是.如右图所示,不是棱柱.
问题2:有两个面互相平行,其余各面都是平行四边形的几何体是棱柱吗?
答:不一定是.如右图所示,不是棱柱.
2.两个底面与平行于底面的截面是全等的多边形;
3.过不相邻的两条侧棱的截面是平行四边形.
1.侧棱都相等,侧面是平行四边形;
棱柱的性质
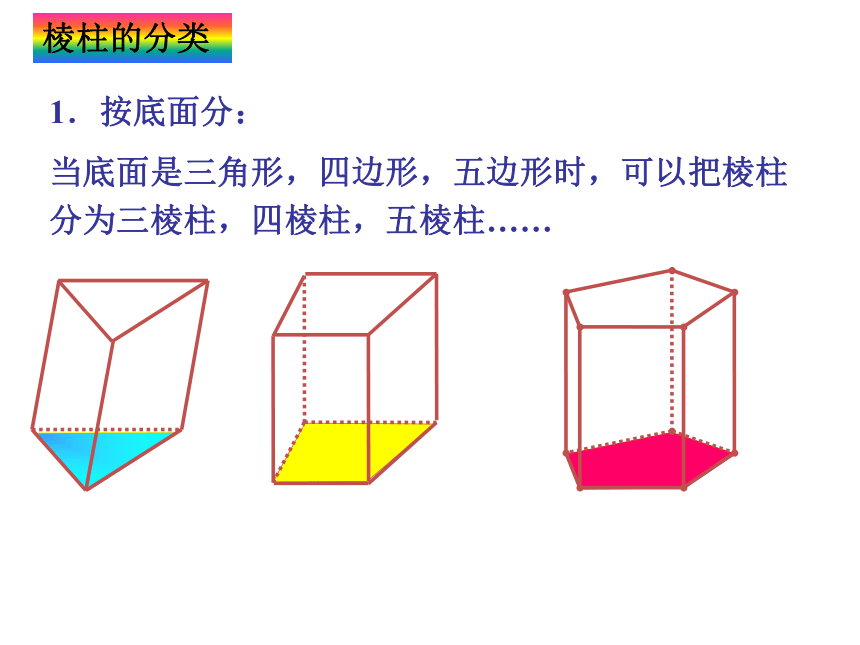
1.按底面分:
棱柱的分类
当底面是三角形,四边形,五边形时,可以把棱柱分为三棱柱,四棱柱,五棱柱……
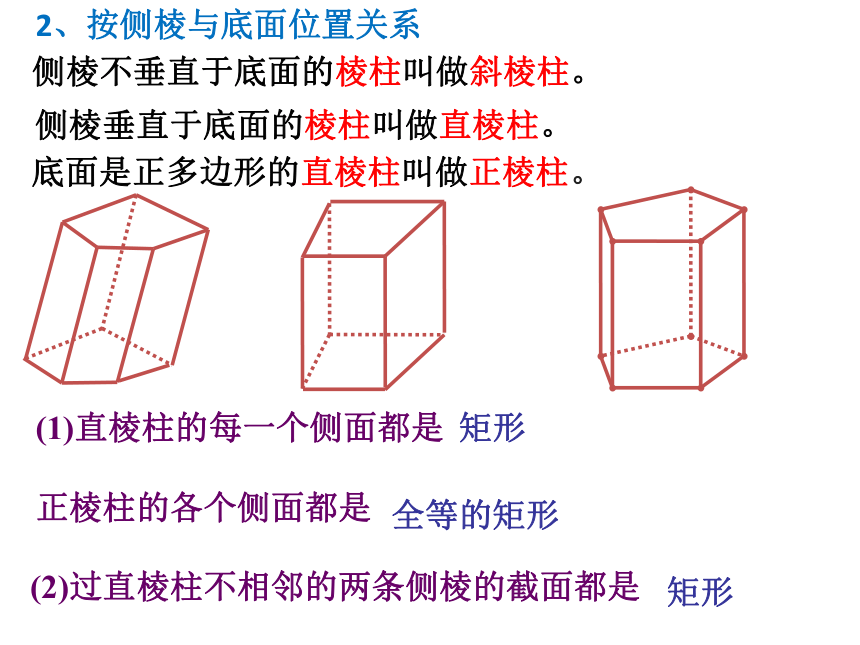
侧棱不垂直于底面的棱柱叫做斜棱柱。
侧棱垂直于底面的棱柱叫做直棱柱。
底面是正多边形的直棱柱叫做正棱柱。
2、按侧棱与底面位置关系
(1)直棱柱的每一个侧面都是
正棱柱的各个侧面都是
(2)过直棱柱不相邻的两条侧棱的截面都是
矩形
全等的矩形
矩形
练习
1、判断下列命题是否正确:
A.有两个侧面是矩形的棱柱是直棱柱;
B.有一个侧面垂直于底面的棱柱是直棱柱;
C.有一条侧棱垂直于底面的两条边的棱柱是直棱柱;
2、一个棱柱是正四棱柱的条件是:
A.底面是正方形,有两个侧面是矩形;
B.底面是正方形,有两个侧面垂直于底面;
C.底面是菱形,且有一个顶点处的三条棱两两垂直;
D.每个侧面都是全等的矩形的四棱柱
D
错
错
错
平行六面体:底面是平行四边形的四棱柱
直平行六面体:侧棱与底面垂直的平行六面体
长方体:底面是矩形的直平行六面体
正方体:棱长都相等的长方体
特殊的四棱柱
棱锥的概念
定义:如果一个多面体有一个多边形的面,且不在这个面上的棱都有一个公共顶点,那么这个多面体叫做棱锥
S
A
B
C
D
E
O
这个多边形叫做棱锥的底面,其余各面叫做棱锥的侧面,侧面都是三角形
不在底面上的棱叫做棱锥的侧棱
侧棱的公共点叫做棱锥的顶点,
顶点与底面之间的距离叫做棱锥的高
棱锥的表示
用顶点及底面各顶点字母表示棱锥,如:五棱锥S-ABCDE
特殊的棱锥-正棱锥
定义:如果棱锥的底面是正多边形,并且底面中心与顶点的连线垂直于底面,这样的棱锥叫正棱锥
正三棱锥(正四面体)
正五棱锥
(正多边形的外接圆(内切圆)圆心叫正多边形中心)
O
S
A
B
C
D
E
F
H
正棱锥的性质
(1)、各侧棱相等,各侧面都是全等的等腰三角形。 各等腰三角形底边上的高相等,叫做正棱锥的斜高
(2)、正棱锥的高、斜高和斜高在底面内的射影 组成 一个直角三角形;正棱锥的高、侧棱、侧棱在 底面内的射影也组成一个直角三角形。
(3)、正棱锥侧棱与底面所成的角 都相等,侧面与底面所成的二面角都相等
练习:判断题
1、一个三棱锥,如果它的底面是直角三角形,那么他的三个侧面都可能是直角三角形
2、侧棱与底面所成角相等的棱锥是正棱锥
3、相邻两侧面所成角相等的棱锥是正棱锥
4、侧棱长相等,各侧面与底面所成的角相等的棱锥是正棱锥
5、三个侧面是全等的等腰三角形的三棱锥是正三棱锥
多面体概念
由若干个平面多边形围成的封闭体称为多面体。
围成多面体的各个多边形称为多面体的面,
食盐
明矾
石膏
两个面的公共边叫做多面体的棱,
棱与棱的公共点叫做多面体的顶点。
多面体分类
按多面体面数分为四面体、五面体、六面体等
定义:有两个面互相平行且全等,且不在这两个面上的棱互相平行,这样的多面体叫做棱柱.
不在底面上的棱叫做棱柱的侧棱.
两个互相平行的平面叫做棱柱的底面,
棱柱的概念
A
B
C
D
D1
E1
A1
B1
C1
E
H
其余各面叫做棱柱的侧面.
两个底面的距离叫做棱柱的高.
不在同一个面上的两个顶点的连线
叫做棱柱的对角线,
棱柱的表示法
棱柱ABCDE- A1B1C1D1E1
棱柱的结构特征
D
A
B
C
E
F
F’
A’
E’
D’
B’
C’
(1)底面互相平行。
(补)侧面是平行四边形。
(2)侧棱相互平行。
由于底面互相平行,所以底面与侧面的交线互相平行
由于侧棱互相平行,
所以侧面是平行四边形
问题1:有两个面互相平行,其余各面都是四边形的几何体是棱柱吗?
答:不一定是.如右图所示,不是棱柱.
问题2:有两个面互相平行,其余各面都是平行四边形的几何体是棱柱吗?
答:不一定是.如右图所示,不是棱柱.
2.两个底面与平行于底面的截面是全等的多边形;
3.过不相邻的两条侧棱的截面是平行四边形.
1.侧棱都相等,侧面是平行四边形;
棱柱的性质
1.按底面分:
棱柱的分类
当底面是三角形,四边形,五边形时,可以把棱柱分为三棱柱,四棱柱,五棱柱……
侧棱不垂直于底面的棱柱叫做斜棱柱。
侧棱垂直于底面的棱柱叫做直棱柱。
底面是正多边形的直棱柱叫做正棱柱。
2、按侧棱与底面位置关系
(1)直棱柱的每一个侧面都是
正棱柱的各个侧面都是
(2)过直棱柱不相邻的两条侧棱的截面都是
矩形
全等的矩形
矩形
练习
1、判断下列命题是否正确:
A.有两个侧面是矩形的棱柱是直棱柱;
B.有一个侧面垂直于底面的棱柱是直棱柱;
C.有一条侧棱垂直于底面的两条边的棱柱是直棱柱;
2、一个棱柱是正四棱柱的条件是:
A.底面是正方形,有两个侧面是矩形;
B.底面是正方形,有两个侧面垂直于底面;
C.底面是菱形,且有一个顶点处的三条棱两两垂直;
D.每个侧面都是全等的矩形的四棱柱
D
错
错
错
平行六面体:底面是平行四边形的四棱柱
直平行六面体:侧棱与底面垂直的平行六面体
长方体:底面是矩形的直平行六面体
正方体:棱长都相等的长方体
特殊的四棱柱
棱锥的概念
定义:如果一个多面体有一个多边形的面,且不在这个面上的棱都有一个公共顶点,那么这个多面体叫做棱锥
S
A
B
C
D
E
O
这个多边形叫做棱锥的底面,其余各面叫做棱锥的侧面,侧面都是三角形
不在底面上的棱叫做棱锥的侧棱
侧棱的公共点叫做棱锥的顶点,
顶点与底面之间的距离叫做棱锥的高
棱锥的表示
用顶点及底面各顶点字母表示棱锥,如:五棱锥S-ABCDE
特殊的棱锥-正棱锥
定义:如果棱锥的底面是正多边形,并且底面中心与顶点的连线垂直于底面,这样的棱锥叫正棱锥
正三棱锥(正四面体)
正五棱锥
(正多边形的外接圆(内切圆)圆心叫正多边形中心)
O
S
A
B
C
D
E
F
H
正棱锥的性质
(1)、各侧棱相等,各侧面都是全等的等腰三角形。 各等腰三角形底边上的高相等,叫做正棱锥的斜高
(2)、正棱锥的高、斜高和斜高在底面内的射影 组成 一个直角三角形;正棱锥的高、侧棱、侧棱在 底面内的射影也组成一个直角三角形。
(3)、正棱锥侧棱与底面所成的角 都相等,侧面与底面所成的二面角都相等
练习:判断题
1、一个三棱锥,如果它的底面是直角三角形,那么他的三个侧面都可能是直角三角形
2、侧棱与底面所成角相等的棱锥是正棱锥
3、相邻两侧面所成角相等的棱锥是正棱锥
4、侧棱长相等,各侧面与底面所成的角相等的棱锥是正棱锥
5、三个侧面是全等的等腰三角形的三棱锥是正三棱锥
