高中数学人教A版必修一2.1.2 指数函数及其性质 课件(44张PPT)
文档属性
| 名称 | 高中数学人教A版必修一2.1.2 指数函数及其性质 课件(44张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 00:00:00 | ||
图片预览









文档简介
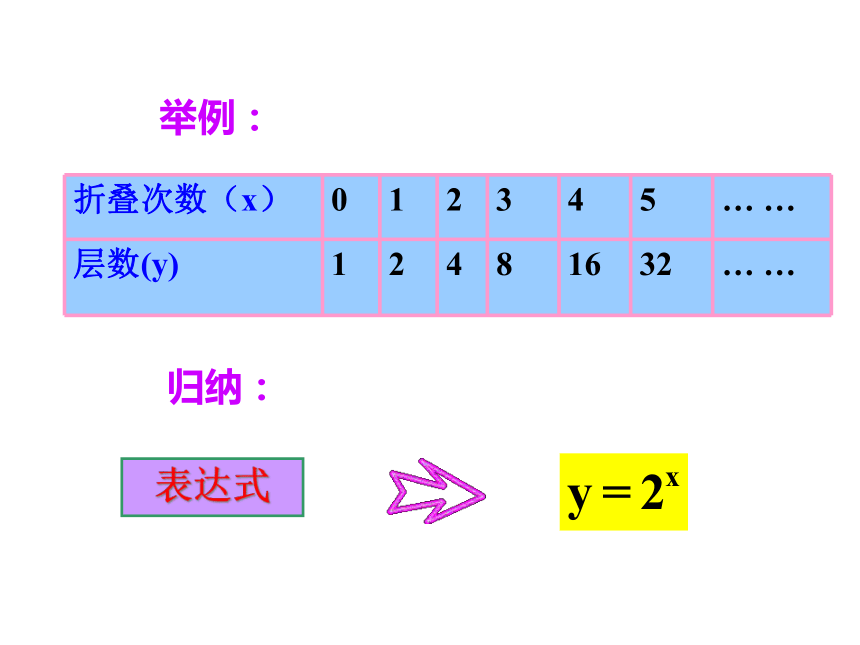
一张白纸对折一次得两层,对折两次得4层,对折3次得8层,问若对折 x 次所得层数为y,则y与x 的函数表达式是?
可以准确写出来吗?
新课导入
问题1.
表达式
举例:
归纳:
折叠次数(x)
0
1
2
3
4
5
… …
层数(y)
1
2
4
8
16
32
… …
当生物死后,它机体内原有的碳-14会按确定的规律衰减,大约每经过5730年衰减为原来的一半,这个时间称为‘‘半衰期”.根据此规律,人们获得了生物体内碳-14含量P 与死亡年数t之间的关系式:
问题2.
1
0
x
y
1.掌握指数函数的定义.
2.掌握指数函数的图像和性质.
3.通过数形结合,利用图象来认识,掌握函数的性质;增强学生分析问题,解决问题的能力.
知识与能力
教学目标
1.培养能够画出函数图像,探索函数性质的过程.
2.培养并体会通过建立数形结合研究函数.
过程与方法
1.经历和体验数学活动的过程以及数学在现实生活中的应用,树立学好数学的信心.
2.通过课堂学习培养敢于实践,勇于发现,大胆探索,合作创新的精神.
3.在探索函数图像和性质过程中,能够通过数形结合,进行全面的概况和总结.
情感态度与价值观
1.指数函数的概.
2. 指数函数的图像和性质.
重点
教学重难点
用数形结合方法从具体到一般地探索、概括指数函数的性质.
难点
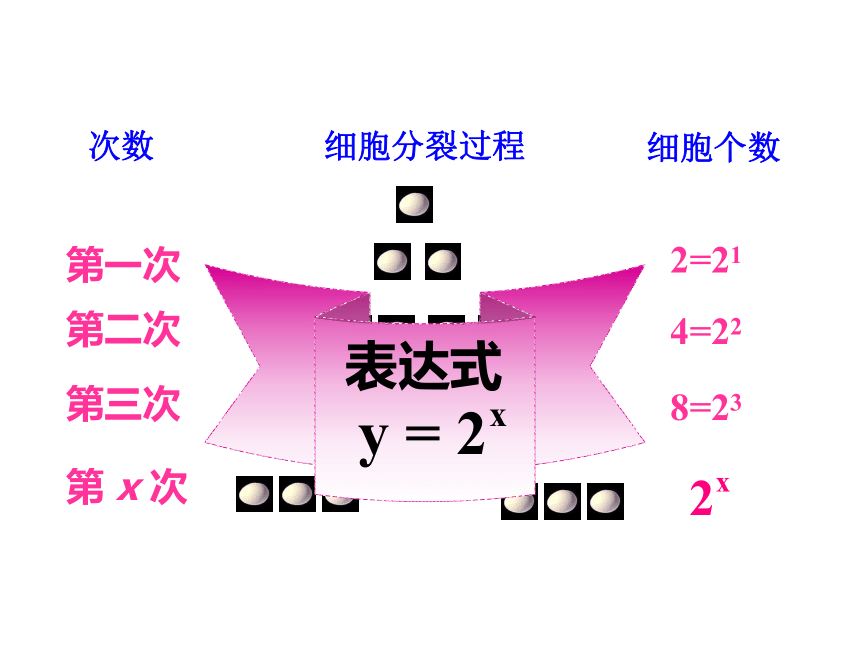
引例:某种细胞分裂时,由1个分裂成2个,2个分裂成4个,……. 1个这样的细胞分裂 x 次后,得到的细胞个数 y 与 x 的函数表达式是:
探究
次数
细胞分裂过程
细胞个数
第一次
第二次
第三次
2=21
4=22
8=23
第 x 次
……
表达式
观 察
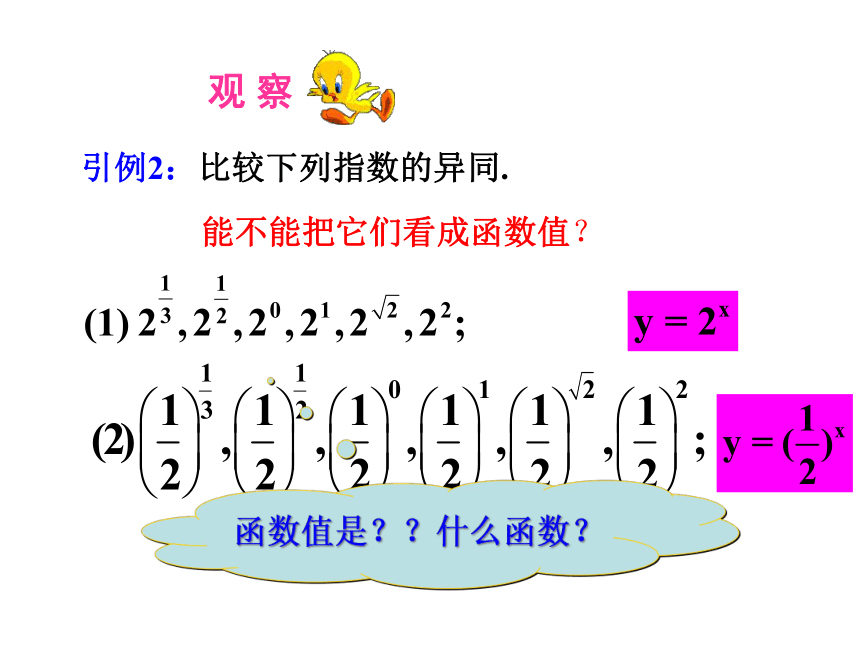
引例2:比较下列指数的异同.
能不能把它们看成函数值?
函数值是??什么函数?
我们从以上两个引例中,抽象得到两个函数:
这两个函数有何特点?
解析式
共同特征
探究
指数幂形式
自变量在指数位置
底数是常量
知识要点
指数函数定义:
形如y = ax ( a?0,且a ?1)的函数叫做指数函数,其中x是自变量 .函数的定义域是R .
何规定a?0,且a?1?
?
?
0
1
a
思考
讨论:
当a<0时,a x有些会没有意义,如
当a=0时, a x有些会没有意义,如
当a=1时,a x 恒等于1,没有研究的必要.
a?0,且 a?1.
小练习
判断下例函数哪些是指数函数?
不是
是
不是
不是
不是
是
随着人民生活水平的提高,汽车的使用也越来越普遍,根据08年发改委发布的《未来我国汽车需求分析报告》判断,今后汽车需求量的年平均增长率预计可达到 7% .那么以后各年汽车需求量将是08年的多少倍?
即
解:由对应关系可知,函数关系式为
知识要点
指数函数图像:
(见下图)
用描点法作函数
动动手
1.列表
x
…
-3
-2
-1
0
1
2
3
…
y=2x
…
1/8
1/4
1/2
1
2
4
8
…
y=3x
…
1/27
1/9
1/3
1
3
9
27
…
2.描点
3.连线
x
y
1
2
3
-1
-2
-3
0
3
9
15
21
27
用描点法作函数
动动手
1.列表
x
…
-3
-2
-1
0
1
2
3
…
y=2-x
…
8
4
2
1
1/2
1/4
1/8
…
y=3-x
…
27
9
3
1
1/3
1/9
1/27
…
思考:若不用描点法,
这两个函数的图象又该
如何作出呢?
2.描点
3.连线
y=1
x
y
1
2
3
-1
-2
-3
0
1
3
5
7
9
27
观 察
这四个图像有何特点?
特点:
y=ax(a>1)与 y=ax(0回答问题
问题一:图象分别在哪几个象限?
答:四个图象都在第____象限
Ⅰ、Ⅱ
问题二:图象的上升、下降与底数a有联系吗?
答:当底数a__时图象上升,底数a由大变小时函数图像____(变化趋势);当底数a______时图象下降.底数a由大变小时函数图像____(变化趋势)
>1
1>a>0
平坦
陡峭
问题三:图象有哪些特殊的点?
答:四个图象都经过点____.
(0,1)
问题四:图象定义域和值域范围?
答:定义域为__.值域为____.
R
(0, +∞)
知识要点
指数函数性质:
(见下表)
a>1
0 图 象
(0,1)
y=1
y
x
y=ax
(a>1)
x
y
y=ax
(0 性 质
定 义 域 :
R
值 域 :
( 0 , + ∞ )
必过 点:
( 0 , 1 )
x>0,y>1;
x<0, 0在 R 上是
增函数
x<0,y>1;
x>0,0在 R 上是
减函数
小练习
求下列函数的定义域:
解:
①
③
②
①
②
③
比较下列两组数的大小:
解:
探究总结
比较指数大小——常用方法,如下
① 构造函数法:要点是利用指数函数的单调性.数的特征是同底不同指(包括可以化为同底的),若底数是参变量需要注意分类讨论.
② 搭桥比较法:用别的数如0或1做桥.数的特征是不同底不同指.
课堂小结
1、指数函数概念
函数y = ax(a?0,且a ?1)叫做指数函数,其中x是自变量 .
函数的定义域是R .
◆方法指导:
研究指数函数时,将a分为a>1和02、指数函数图像
(a>1)
(0,1)
y=1
y=ax
(a>1)
(0y=ax
(0(0,1)
y=1
y
x
y
x
3、指数函数性质
◆方法指导
利用函数图像研究函数性质是一种直观而形象的方法,记忆指数函数性质时可以联想它的图像.
(1)定义域: 值 域:
(2)函数的特殊值:
(3)函数的单调性:
高考链接
1.(2007 上海)方程 的解是________.
x= - 1
解析 : ,∴x-1=-2, ∴x=-1
2.(2009 山东) 函数 的图像大致为( )
1
x
y
1
O
A
x
y
O
1
1
B
x
y
O
1
1
C
x
y
1
1
D
O
A
解析:函数有意义,需要使 其定义域为 ,排除C、D,又因为
所以当时x>0时函数为减函数
3.(2007 辽宁)设函数f(x)定义在实数集上,它的图像关于直线x=1对称,且当x≥1时,f(x)=
则有( )
B
解析:利用对称性,三点到直线x=1距离越远越大.
随堂练习
1.求下列函数的定义域:
解:
2.比较下列各组数的大小:
解:
3.求满足条件的值:
解:
讨论:
解:
(1)当a<0时,没有意义.
(2)当a=1时,x=-1/5时, y1≡y2.
(3)当0-1/5时,y1y2.
(4)当a>1时,y=ax在R增函数; x=-1/5时, y1=y2; x>-1/5时,y1>y2; x<-1/5时,y1上题中,若把 2/3 改为a可不可以?怎么做?
习题答案
练习(第58页)
1.图(略)见课上ppt.
2.(1){x|x≥2};(2) {x|x≠0};
3. y=2x (x∈N*).
可以准确写出来吗?
新课导入
问题1.
表达式
举例:
归纳:
折叠次数(x)
0
1
2
3
4
5
… …
层数(y)
1
2
4
8
16
32
… …
当生物死后,它机体内原有的碳-14会按确定的规律衰减,大约每经过5730年衰减为原来的一半,这个时间称为‘‘半衰期”.根据此规律,人们获得了生物体内碳-14含量P 与死亡年数t之间的关系式:
问题2.
1
0
x
y
1.掌握指数函数的定义.
2.掌握指数函数的图像和性质.
3.通过数形结合,利用图象来认识,掌握函数的性质;增强学生分析问题,解决问题的能力.
知识与能力
教学目标
1.培养能够画出函数图像,探索函数性质的过程.
2.培养并体会通过建立数形结合研究函数.
过程与方法
1.经历和体验数学活动的过程以及数学在现实生活中的应用,树立学好数学的信心.
2.通过课堂学习培养敢于实践,勇于发现,大胆探索,合作创新的精神.
3.在探索函数图像和性质过程中,能够通过数形结合,进行全面的概况和总结.
情感态度与价值观
1.指数函数的概.
2. 指数函数的图像和性质.
重点
教学重难点
用数形结合方法从具体到一般地探索、概括指数函数的性质.
难点
引例:某种细胞分裂时,由1个分裂成2个,2个分裂成4个,……. 1个这样的细胞分裂 x 次后,得到的细胞个数 y 与 x 的函数表达式是:
探究
次数
细胞分裂过程
细胞个数
第一次
第二次
第三次
2=21
4=22
8=23
第 x 次
……
表达式
观 察
引例2:比较下列指数的异同.
能不能把它们看成函数值?
函数值是??什么函数?
我们从以上两个引例中,抽象得到两个函数:
这两个函数有何特点?
解析式
共同特征
探究
指数幂形式
自变量在指数位置
底数是常量
知识要点
指数函数定义:
形如y = ax ( a?0,且a ?1)的函数叫做指数函数,其中x是自变量 .函数的定义域是R .
何规定a?0,且a?1?
?
?
0
1
a
思考
讨论:
当a<0时,a x有些会没有意义,如
当a=0时, a x有些会没有意义,如
当a=1时,a x 恒等于1,没有研究的必要.
a?0,且 a?1.
小练习
判断下例函数哪些是指数函数?
不是
是
不是
不是
不是
是
随着人民生活水平的提高,汽车的使用也越来越普遍,根据08年发改委发布的《未来我国汽车需求分析报告》判断,今后汽车需求量的年平均增长率预计可达到 7% .那么以后各年汽车需求量将是08年的多少倍?
即
解:由对应关系可知,函数关系式为
知识要点
指数函数图像:
(见下图)
用描点法作函数
动动手
1.列表
x
…
-3
-2
-1
0
1
2
3
…
y=2x
…
1/8
1/4
1/2
1
2
4
8
…
y=3x
…
1/27
1/9
1/3
1
3
9
27
…
2.描点
3.连线
x
y
1
2
3
-1
-2
-3
0
3
9
15
21
27
用描点法作函数
动动手
1.列表
x
…
-3
-2
-1
0
1
2
3
…
y=2-x
…
8
4
2
1
1/2
1/4
1/8
…
y=3-x
…
27
9
3
1
1/3
1/9
1/27
…
思考:若不用描点法,
这两个函数的图象又该
如何作出呢?
2.描点
3.连线
y=1
x
y
1
2
3
-1
-2
-3
0
1
3
5
7
9
27
观 察
这四个图像有何特点?
特点:
y=ax(a>1)与 y=ax(0
问题一:图象分别在哪几个象限?
答:四个图象都在第____象限
Ⅰ、Ⅱ
问题二:图象的上升、下降与底数a有联系吗?
答:当底数a__时图象上升,底数a由大变小时函数图像____(变化趋势);当底数a______时图象下降.底数a由大变小时函数图像____(变化趋势)
>1
1>a>0
平坦
陡峭
问题三:图象有哪些特殊的点?
答:四个图象都经过点____.
(0,1)
问题四:图象定义域和值域范围?
答:定义域为__.值域为____.
R
(0, +∞)
知识要点
指数函数性质:
(见下表)
a>1
0
(0,1)
y=1
y
x
y=ax
(a>1)
x
y
y=ax
(0
定 义 域 :
R
值 域 :
( 0 , + ∞ )
必过 点:
( 0 , 1 )
x>0,y>1;
x<0, 0
增函数
x<0,y>1;
x>0,0
减函数
小练习
求下列函数的定义域:
解:
①
③
②
①
②
③
比较下列两组数的大小:
解:
探究总结
比较指数大小——常用方法,如下
① 构造函数法:要点是利用指数函数的单调性.数的特征是同底不同指(包括可以化为同底的),若底数是参变量需要注意分类讨论.
② 搭桥比较法:用别的数如0或1做桥.数的特征是不同底不同指.
课堂小结
1、指数函数概念
函数y = ax(a?0,且a ?1)叫做指数函数,其中x是自变量 .
函数的定义域是R .
◆方法指导:
研究指数函数时,将a分为a>1和0
(a>1)
(0,1)
y=1
y=ax
(a>1)
(0
(0
y=1
y
x
y
x
3、指数函数性质
◆方法指导
利用函数图像研究函数性质是一种直观而形象的方法,记忆指数函数性质时可以联想它的图像.
(1)定义域: 值 域:
(2)函数的特殊值:
(3)函数的单调性:
高考链接
1.(2007 上海)方程 的解是________.
x= - 1
解析 : ,∴x-1=-2, ∴x=-1
2.(2009 山东) 函数 的图像大致为( )
1
x
y
1
O
A
x
y
O
1
1
B
x
y
O
1
1
C
x
y
1
1
D
O
A
解析:函数有意义,需要使 其定义域为 ,排除C、D,又因为
所以当时x>0时函数为减函数
3.(2007 辽宁)设函数f(x)定义在实数集上,它的图像关于直线x=1对称,且当x≥1时,f(x)=
则有( )
B
解析:利用对称性,三点到直线x=1距离越远越大.
随堂练习
1.求下列函数的定义域:
解:
2.比较下列各组数的大小:
解:
3.求满足条件的值:
解:
讨论:
解:
(1)当a<0时,没有意义.
(2)当a=1时,x=-1/5时, y1≡y2.
(3)当0
(4)当a>1时,y=ax在R增函数; x=-1/5时, y1=y2; x>-1/5时,y1>y2; x<-1/5时,y1
习题答案
练习(第58页)
1.图(略)见课上ppt.
2.(1){x|x≥2};(2) {x|x≠0};
3. y=2x (x∈N*).
