高中数学人教A版选修1-1第三章3.3.1函数的单调性与导数 课件(29张PPT)
文档属性
| 名称 | 高中数学人教A版选修1-1第三章3.3.1函数的单调性与导数 课件(29张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 00:00:00 | ||
图片预览





文档简介
3.3.1 函数的单调性与导数
3.3导数在研究函数中的应用
(4)对数函数的导数:
(5)指数函数的导数:
(3)三角函数 :
(1)常函数:(C)/ ? 0,(c为常数);
(2)幂函数 : (xn)/ ? nxn?1
一、复习回顾:基本初等函数的导数公式:
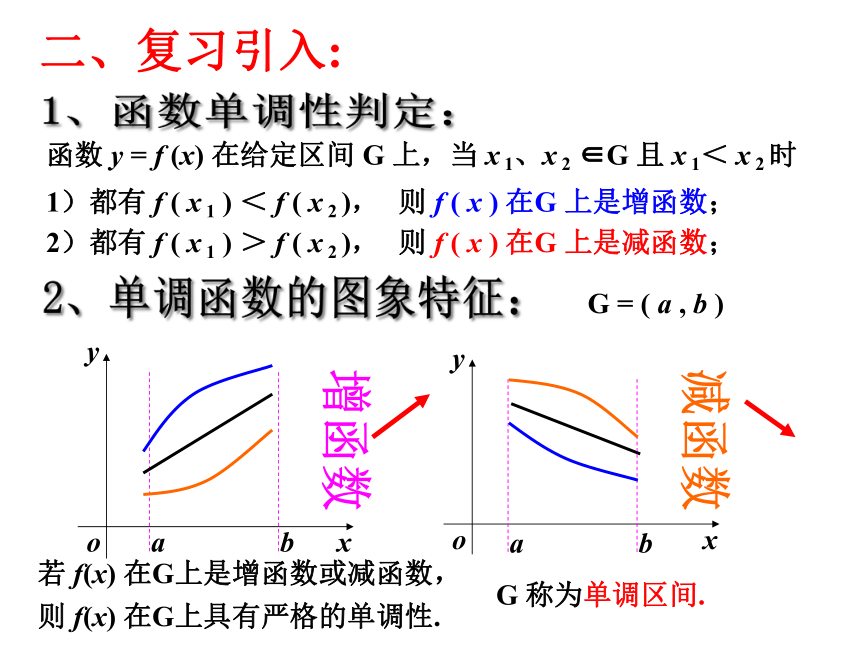
函数 y = f (x) 在给定区间 G 上,当 x 1、x 2 ∈G 且 x 1< x 2 时
y
x
o
a
b
y
x
o
a
b
1)都有 f ( x 1 ) < f ( x 2 ),
则 f ( x ) 在G 上是增函数;
2)都有 f ( x 1 ) > f ( x 2 ),
则 f ( x ) 在G 上是减函数;
若 f(x) 在G上是增函数或减函数,
则 f(x) 在G上具有严格的单调性.
G 称为单调区间.
G = ( a , b )
二、复习引入:
(1)函数的单调性也叫函数的增减性;
(2)函数的单调性是对某个区间而言的,它是个局部概
念;这个区间是定义域的子集.
(3)单调区间:针对自变量x而言的.
若函数在此区间上是增函数,则为单调递增区间;
若函数在此区间上是减函数,则为单调递减区间.
以前,我们用定义来判断函数的单调性.在假设x1观察:
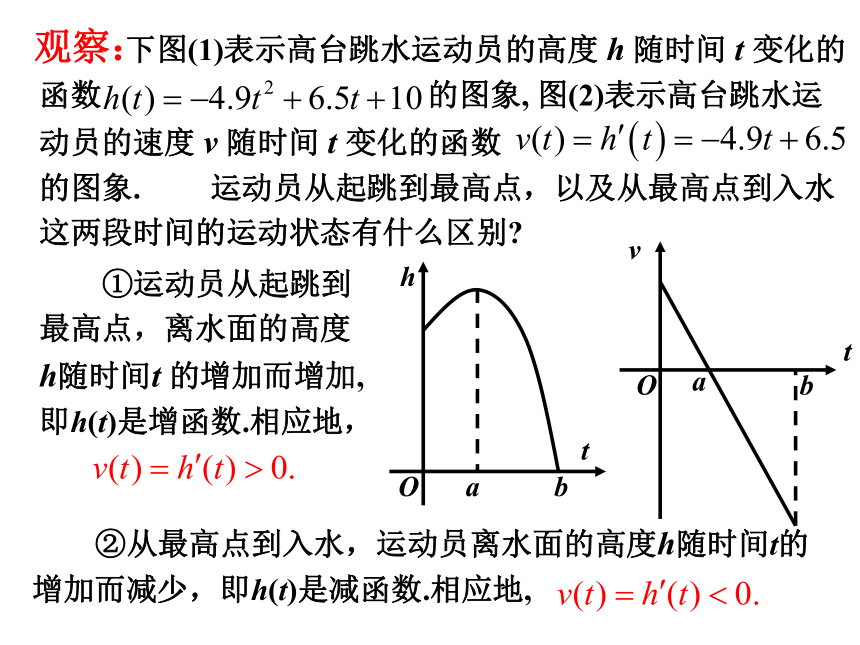
下图(1)表示高台跳水运动员的高度 h 随时间 t 变化的函数 的图象, 图(2)表示高台跳水运动员的速度 v 随时间 t 变化的函数 的图象. 运动员从起跳到最高点,以及从最高点到入水这两段时间的运动状态有什么区别?
a
a
b
b
t
t
v
h
O
O
①运动员从起跳到最高点,离水面的高度h随时间t 的增加而增加,即h(t)是增函数.相应地,
②从最高点到入水,运动员离水面的高度h随时间t的增加而减少,即h(t)是减函数.相应地,
(1)
(2)
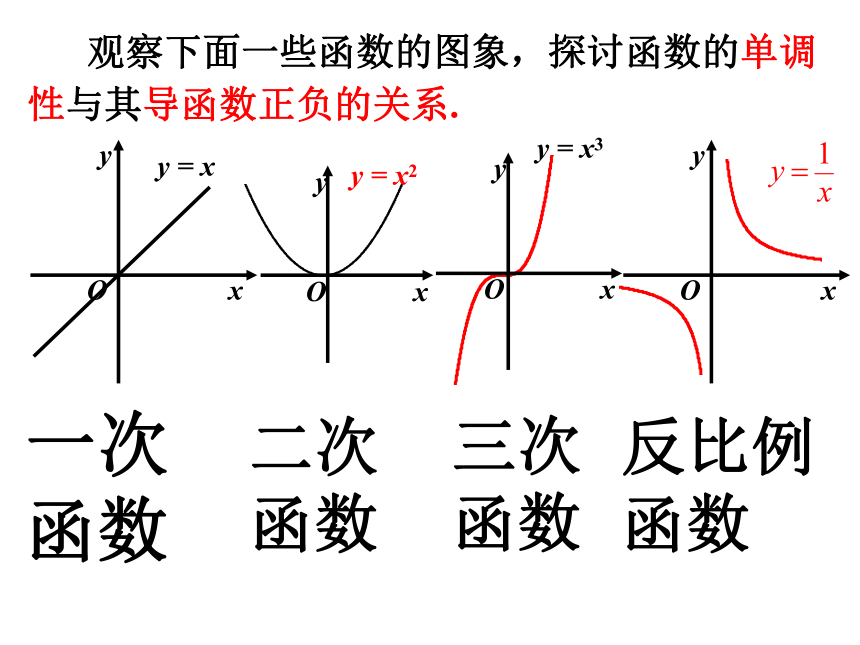
观察下面一些函数的图象,探讨函数的单调性与其导函数正负的关系.
一次函数
二次函数
三次函数
反比例函数
y = x2
x
y
O
y = x3
x
y
O
x
y
O
x
y
O
y = x
x
y
O
y = x2
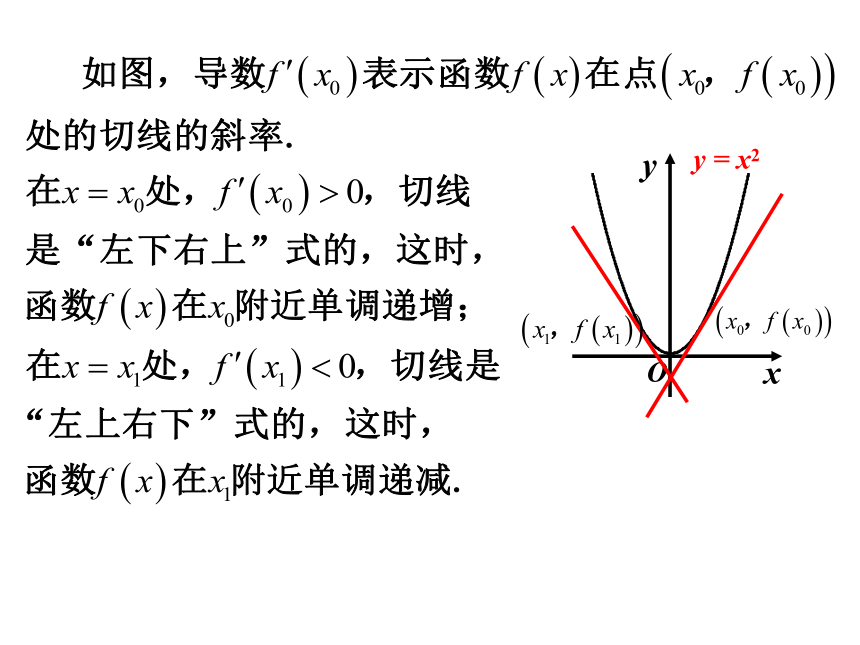
一般地,函数的单调性与其导函数的正负有如下关系:
在某个区间(a,b)内,如果 ,那么函数 在这个区间内单调递增; 如果 ,那么函数 在这个区间内单调递减.
常数函数
P90思考?
例1 、 已知导函数 的下列信息:
当1 < x < 4 时,
当 x > 4 , 或 x < 1时,
当 x = 4 , 或 x = 1时,
试画出函数 的图象的大致形状.
解:当1 < x < 4 时, 可知 在此区间内单调递增;
当 x > 4 , 或 x < 1时, 可知 在此区间内单调递减;
当 x = 4 , 或 x = 1时,
综上, 函数 图象的大致形状如右图所示.
x
y
O
1
4
临近点
临近点
例2 、 判断下列函数的单调性, 并求出单调区间:
解:(1) 因为 , 所以
因此, 函数 在 上单调递增.
(2) 因为 , 所以
当 , 即 时, 函数 单调递增;
当 , 即 时, 函数 单调递减.
例2 、判断下列函数的单调性, 并求出单调区间:
解:(3) 因为 , 所以
因此, 函数 在 上单调递减.
(4) 因为 , 所以
当 , 即 时, 函数 单调递减.
当 , 即 时, 函数 单调递增;
例3 、如图, 水以常速(即单位时间内注入水的体积相同)注入下面四种底面积相同的容器中, 请分别找出与各容器对应的水的高度h与时间t的函数关系图象.
(A)
(B)
(C)
(D)
h
t
O
分析:以容器(2)为例,由于容器上细下粗,所以水以常速注入时,开始阶段高度增加得慢,以后高度增加得越来越快,反映在图象(A)上.
h
t
O
h
t
O
h
t
O
(1)
(2)
(3)
(4)
思考:一般地, 如果一个函数在某一范围内导数的绝对值较大, 那么函数在这个范围内变化得快, 这时, 函数的图象就比较“陡峭”(向上或向下); 反之, 函数的图象就“平缓”一些.
如图,函数 在 或 内的图象“陡峭”,在 或
内的图象平缓.
求可导函数f(x)单调区间的步骤:
(1)求f’(x);
(2)解不等式f’(x)>0或f’(x)<0;
(3)确认并指出递增区间(或递减区间).
证明可导函数f(x)在(a,b)内的单调性的方法:
(1)求f’(x);
(2)确认f’(x)在(a,b)内的符号;
(3)作出结论.
练习:P93
1、判断下列函数的单调性,并求出单调区间:
练习:P93
2、函数 的图象如图所示, 试画出导函数 图象 的大致形状
练习:P93
3、讨论二次函数 的单调区间.
解:
由 , 得 , 即函数 的递增区间是 ; 相应地, 函数的递减区间是
由 , 得 , 即函数 的递增区间是 ; 相应地, 函数的递减区间是
练习:P93
4、求证: 函数 在 内是减函数.
解:
由 , 解得 , 所以函数 的递减区间是 , 即函数 在 内是减函数.
题型一 利用导数求参数的取值范围
解:由已知得
因为函数在(0,1]上单调递增,
本题用到一个重要的转化:
最值定理
练习:
题型二 方程根的问题:
例3、求证:方程 只有一个根.
题型三 构造函数证明不等式
作业:已知函数f(x)=ax?+3x?-x+1在R
上是减函数,求a的取值范围.
P98 习题3.3 A组1、2
B组 1(1)(2)(3)(4)
3.3导数在研究函数中的应用
(4)对数函数的导数:
(5)指数函数的导数:
(3)三角函数 :
(1)常函数:(C)/ ? 0,(c为常数);
(2)幂函数 : (xn)/ ? nxn?1
一、复习回顾:基本初等函数的导数公式:
函数 y = f (x) 在给定区间 G 上,当 x 1、x 2 ∈G 且 x 1< x 2 时
y
x
o
a
b
y
x
o
a
b
1)都有 f ( x 1 ) < f ( x 2 ),
则 f ( x ) 在G 上是增函数;
2)都有 f ( x 1 ) > f ( x 2 ),
则 f ( x ) 在G 上是减函数;
若 f(x) 在G上是增函数或减函数,
则 f(x) 在G上具有严格的单调性.
G 称为单调区间.
G = ( a , b )
二、复习引入:
(1)函数的单调性也叫函数的增减性;
(2)函数的单调性是对某个区间而言的,它是个局部概
念;这个区间是定义域的子集.
(3)单调区间:针对自变量x而言的.
若函数在此区间上是增函数,则为单调递增区间;
若函数在此区间上是减函数,则为单调递减区间.
以前,我们用定义来判断函数的单调性.在假设x1
下图(1)表示高台跳水运动员的高度 h 随时间 t 变化的函数 的图象, 图(2)表示高台跳水运动员的速度 v 随时间 t 变化的函数 的图象. 运动员从起跳到最高点,以及从最高点到入水这两段时间的运动状态有什么区别?
a
a
b
b
t
t
v
h
O
O
①运动员从起跳到最高点,离水面的高度h随时间t 的增加而增加,即h(t)是增函数.相应地,
②从最高点到入水,运动员离水面的高度h随时间t的增加而减少,即h(t)是减函数.相应地,
(1)
(2)
观察下面一些函数的图象,探讨函数的单调性与其导函数正负的关系.
一次函数
二次函数
三次函数
反比例函数
y = x2
x
y
O
y = x3
x
y
O
x
y
O
x
y
O
y = x
x
y
O
y = x2
一般地,函数的单调性与其导函数的正负有如下关系:
在某个区间(a,b)内,如果 ,那么函数 在这个区间内单调递增; 如果 ,那么函数 在这个区间内单调递减.
常数函数
P90思考?
例1 、 已知导函数 的下列信息:
当1 < x < 4 时,
当 x > 4 , 或 x < 1时,
当 x = 4 , 或 x = 1时,
试画出函数 的图象的大致形状.
解:当1 < x < 4 时, 可知 在此区间内单调递增;
当 x > 4 , 或 x < 1时, 可知 在此区间内单调递减;
当 x = 4 , 或 x = 1时,
综上, 函数 图象的大致形状如右图所示.
x
y
O
1
4
临近点
临近点
例2 、 判断下列函数的单调性, 并求出单调区间:
解:(1) 因为 , 所以
因此, 函数 在 上单调递增.
(2) 因为 , 所以
当 , 即 时, 函数 单调递增;
当 , 即 时, 函数 单调递减.
例2 、判断下列函数的单调性, 并求出单调区间:
解:(3) 因为 , 所以
因此, 函数 在 上单调递减.
(4) 因为 , 所以
当 , 即 时, 函数 单调递减.
当 , 即 时, 函数 单调递增;
例3 、如图, 水以常速(即单位时间内注入水的体积相同)注入下面四种底面积相同的容器中, 请分别找出与各容器对应的水的高度h与时间t的函数关系图象.
(A)
(B)
(C)
(D)
h
t
O
分析:以容器(2)为例,由于容器上细下粗,所以水以常速注入时,开始阶段高度增加得慢,以后高度增加得越来越快,反映在图象(A)上.
h
t
O
h
t
O
h
t
O
(1)
(2)
(3)
(4)
思考:一般地, 如果一个函数在某一范围内导数的绝对值较大, 那么函数在这个范围内变化得快, 这时, 函数的图象就比较“陡峭”(向上或向下); 反之, 函数的图象就“平缓”一些.
如图,函数 在 或 内的图象“陡峭”,在 或
内的图象平缓.
求可导函数f(x)单调区间的步骤:
(1)求f’(x);
(2)解不等式f’(x)>0或f’(x)<0;
(3)确认并指出递增区间(或递减区间).
证明可导函数f(x)在(a,b)内的单调性的方法:
(1)求f’(x);
(2)确认f’(x)在(a,b)内的符号;
(3)作出结论.
练习:P93
1、判断下列函数的单调性,并求出单调区间:
练习:P93
2、函数 的图象如图所示, 试画出导函数 图象 的大致形状
练习:P93
3、讨论二次函数 的单调区间.
解:
由 , 得 , 即函数 的递增区间是 ; 相应地, 函数的递减区间是
由 , 得 , 即函数 的递增区间是 ; 相应地, 函数的递减区间是
练习:P93
4、求证: 函数 在 内是减函数.
解:
由 , 解得 , 所以函数 的递减区间是 , 即函数 在 内是减函数.
题型一 利用导数求参数的取值范围
解:由已知得
因为函数在(0,1]上单调递增,
本题用到一个重要的转化:
最值定理
练习:
题型二 方程根的问题:
例3、求证:方程 只有一个根.
题型三 构造函数证明不等式
作业:已知函数f(x)=ax?+3x?-x+1在R
上是减函数,求a的取值范围.
P98 习题3.3 A组1、2
B组 1(1)(2)(3)(4)
