高中数学人教A版选修2-1第二章2.2.1椭圆及其标准方程课件(23张PPT)
文档属性
| 名称 | 高中数学人教A版选修2-1第二章2.2.1椭圆及其标准方程课件(23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 20:04:25 | ||
图片预览





文档简介
学习目标
1.理解椭圆标准方程的推导;
2.掌握椭圆的标准方程;
3.会根据条件求椭圆的标准方程,会根据椭圆的标准方程求焦点坐标。
开普勒行星运动定律
所有行星绕太阳运行的轨道都是______,太阳处_______________.
椭圆
椭圆的一个焦点上
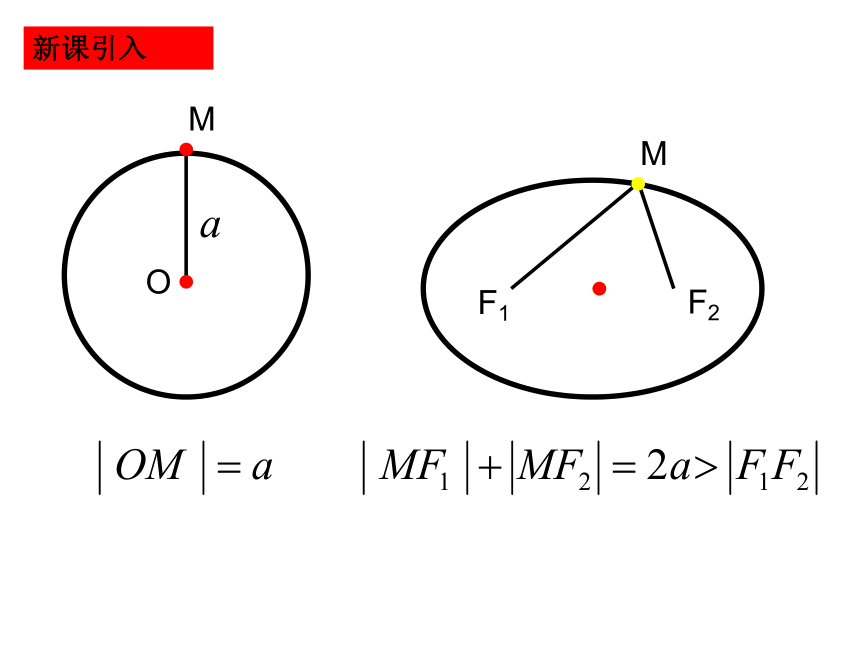
新课引入
M
F1
F2
M
O
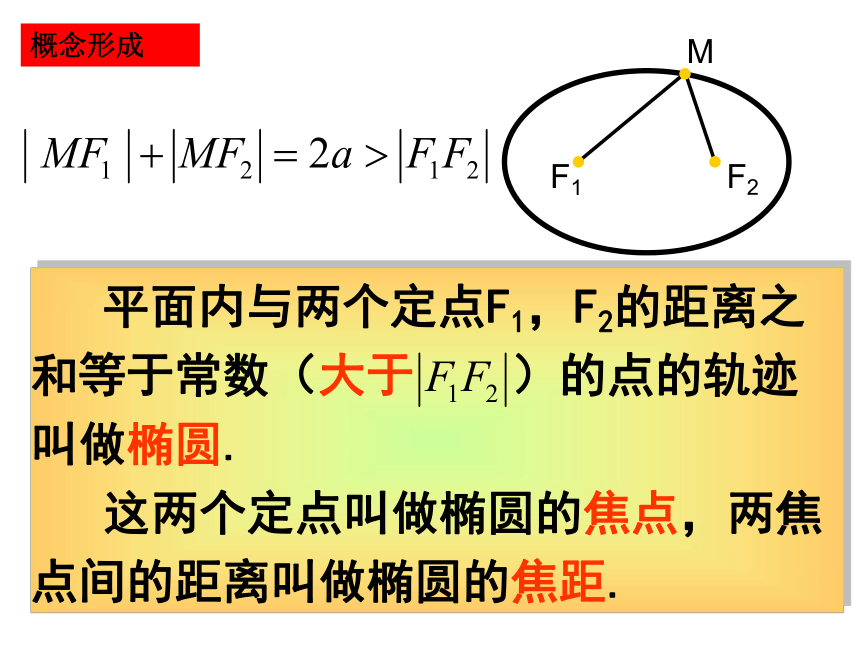
新课引入
M
F1
F2
平面内与两个定点F1,F2的距离之和等于常数(大于 )的点的轨迹叫做椭圆.
这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距.
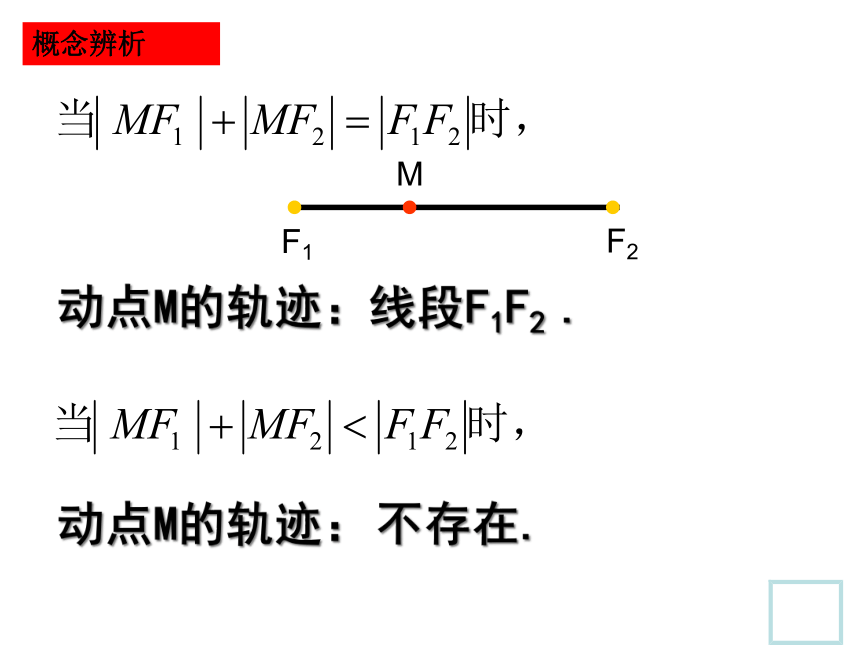
概念形成
动点M的轨迹:
线段F1F2 .
M
F1
F2
动点M的轨迹:
不存在.
概念辨析
用定义判断下列动点M的轨迹是否为椭圆.
(1)到F1(-2,0)、F2(2,0)的距离之和为6的点的轨迹.
(2)到F1(0,-2)、F2(0,2)的距离之和为4的点的轨迹.
(3)到F1(-2,0)、F2(0,2)的距离之和为3的点的轨迹.
是
不是
是
概念辨析
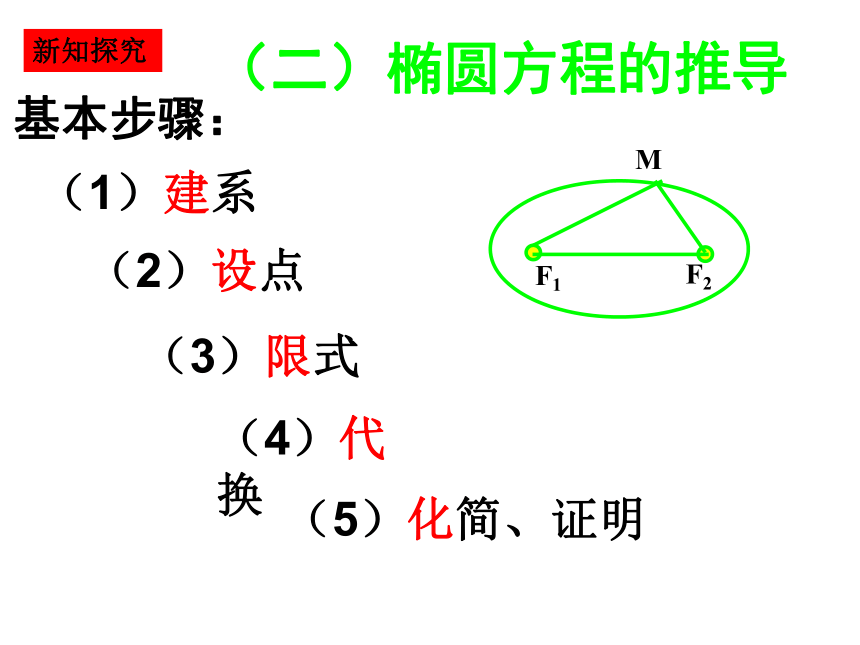
(二)椭圆方程的推导
F1
F2
M
基本步骤:
(1)建系
(2)设点
(3)限式
(4)代换
(5)化简、证明
新知探究
M
F1
F2
新知探究
M
F1
F2
新知探究
P
c
a
b
椭圆的标准方程
形成结论
思考?
F2
F1
M
新知探究
椭圆的标准方程
当焦点在x轴上时:
当焦点在y轴上时:
形成结论
答:在 x 轴上(-3,0)和(3,0)
答:在 y 轴上(0,-5)和(0,5)
答:在y 轴上(0,-1)和(0,1)
判定下列椭圆的焦点在 哪个轴上,并指明a2、b2,写出焦点坐标.
概念辨析
例1 写出适合下列条件的椭圆的标准
方程.
(1)a = 4 , b = 1, 焦点在x轴上.
(2)a = 4 , c = ,焦点在y轴上.
(3)a + b = 10 , c = .
典例讲评
例2 已知椭圆两个焦点的坐标分别
是(-2,0),(2,0),并且经过点 ,求它的标准方程.
典例讲评
求椭圆方程的方法和步骤:
①根据题意,设出标准方程;
(根据焦点的位置设出标准方程)
②根据条件确定a,b的值;
③写出椭圆的方程.
形成结论
(1)椭圆的定义:
课堂小结
(2)标准方程的两种形式:
(3)求椭圆方程.
越练越熟
今日作业
祝你快乐!
1.理解椭圆标准方程的推导;
2.掌握椭圆的标准方程;
3.会根据条件求椭圆的标准方程,会根据椭圆的标准方程求焦点坐标。
开普勒行星运动定律
所有行星绕太阳运行的轨道都是______,太阳处_______________.
椭圆
椭圆的一个焦点上
新课引入
M
F1
F2
M
O
新课引入
M
F1
F2
平面内与两个定点F1,F2的距离之和等于常数(大于 )的点的轨迹叫做椭圆.
这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距.
概念形成
动点M的轨迹:
线段F1F2 .
M
F1
F2
动点M的轨迹:
不存在.
概念辨析
用定义判断下列动点M的轨迹是否为椭圆.
(1)到F1(-2,0)、F2(2,0)的距离之和为6的点的轨迹.
(2)到F1(0,-2)、F2(0,2)的距离之和为4的点的轨迹.
(3)到F1(-2,0)、F2(0,2)的距离之和为3的点的轨迹.
是
不是
是
概念辨析
(二)椭圆方程的推导
F1
F2
M
基本步骤:
(1)建系
(2)设点
(3)限式
(4)代换
(5)化简、证明
新知探究
M
F1
F2
新知探究
M
F1
F2
新知探究
P
c
a
b
椭圆的标准方程
形成结论
思考?
F2
F1
M
新知探究
椭圆的标准方程
当焦点在x轴上时:
当焦点在y轴上时:
形成结论
答:在 x 轴上(-3,0)和(3,0)
答:在 y 轴上(0,-5)和(0,5)
答:在y 轴上(0,-1)和(0,1)
判定下列椭圆的焦点在 哪个轴上,并指明a2、b2,写出焦点坐标.
概念辨析
例1 写出适合下列条件的椭圆的标准
方程.
(1)a = 4 , b = 1, 焦点在x轴上.
(2)a = 4 , c = ,焦点在y轴上.
(3)a + b = 10 , c = .
典例讲评
例2 已知椭圆两个焦点的坐标分别
是(-2,0),(2,0),并且经过点 ,求它的标准方程.
典例讲评
求椭圆方程的方法和步骤:
①根据题意,设出标准方程;
(根据焦点的位置设出标准方程)
②根据条件确定a,b的值;
③写出椭圆的方程.
形成结论
(1)椭圆的定义:
课堂小结
(2)标准方程的两种形式:
(3)求椭圆方程.
越练越熟
今日作业
祝你快乐!
