沪教版(上海)高中数学高二上册第七章7.7数列的极限课件(18张PPT)
文档属性
| 名称 | 沪教版(上海)高中数学高二上册第七章7.7数列的极限课件(18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 00:00:00 | ||
图片预览






文档简介
第7章数列与数学归纳法
本章讨论数列的通项公式、递推公式;讨论两类最常用的数列:等差数列和等比数列以及它们前n项和的问题,并学习数列在实际解决问题中的应用。
§ 数列的极限
一、引例
割圆术
二、概念
数列的极限
三、练习
常用极限&判断
引例
如何计算出π的数值?
用绳子和游标卡尺测量出半径和周长
再精确的测量,也会有误差!
刘徽(约公元225年—295年)
“割之弥细,所失弥少,割之又割,以至不可割,则与圆周合体,而无所失矣。”
——《九章算术》方田章圆田术刘徽注
引例
一般地,在n无限增大的变化过程中,如果无穷数列{an}中的an无限趋近于一个常数A,那么A叫做数列{an}的极限,或叫做数列{an}收敛于A,记作 。
概念
数列的极限概念:
读作“n趋向于无穷大时, {an}的极限等于A”
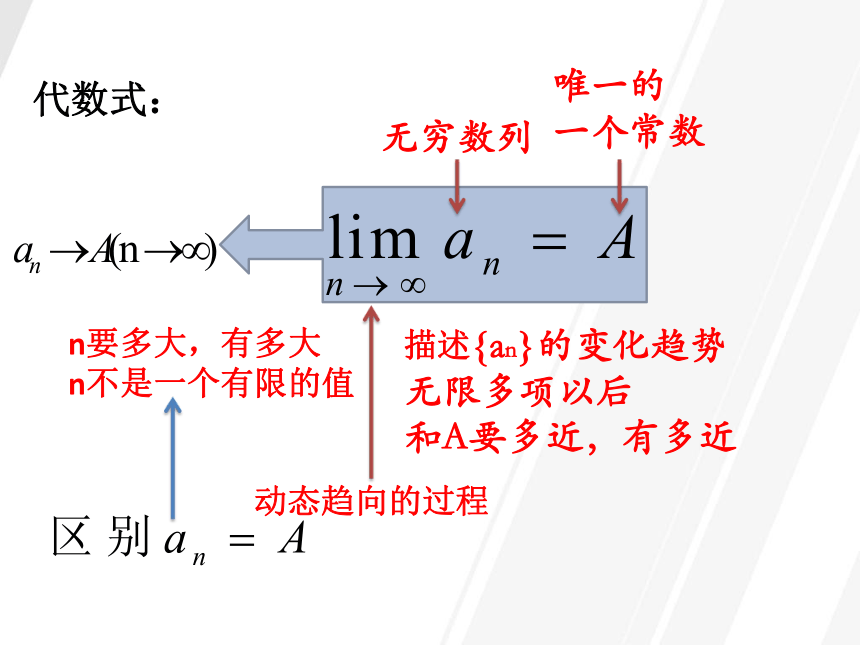
代数式:
无穷数列
动态趋向的过程
n要多大,有多大
n不是一个有限的值
唯一的
一个常数
概念
描述{an}的变化趋势
无限多项以后
和A要多近,有多近
概念
散点图:
在n无限增大的变化过程中, {an}的点和y=A这条直线无限得近。
概念
刘徽(约公元225年—295年)
“割之弥细,所失弥少,割之又割,以至不可割,则与圆周合体,而无所失矣。”
——《九章算术》方田章圆田术刘徽注
练习
庄子(约公元前369年—约公元前286年)
“一尺之棰,日取其半,万世不竭。”
——《庄子 天下篇》
练习
“一尺之棰,日取其半,万世不竭。”
练习
练习
常用极限:
练习
代数:
推广:
特殊:
反例:
练习
{7DF18680-E054-41AD-8BC1-D1AEF772440D}
0.1
3
<0.0625
成立
0.01
6
<0.0078125
成立
0.001
9
<0.0009765625
成立
0.0001
13
<0.00006103515625
成立
0.00001
16
<0.000001525878906
成立
成立
练习:判断下列数列的极限是否存在,
若存在,极限为多少?
练习
练习7.7(1),7.7(2)
1、能不能定量地描述数列的极限?
2、数列的极限能否进行四则运算?
3、了解数列的极限在生活中的应用
4、了解数列的极限发展的数学史
回家作业:
思考:
本章讨论数列的通项公式、递推公式;讨论两类最常用的数列:等差数列和等比数列以及它们前n项和的问题,并学习数列在实际解决问题中的应用。
§ 数列的极限
一、引例
割圆术
二、概念
数列的极限
三、练习
常用极限&判断
引例
如何计算出π的数值?
用绳子和游标卡尺测量出半径和周长
再精确的测量,也会有误差!
刘徽(约公元225年—295年)
“割之弥细,所失弥少,割之又割,以至不可割,则与圆周合体,而无所失矣。”
——《九章算术》方田章圆田术刘徽注
引例
一般地,在n无限增大的变化过程中,如果无穷数列{an}中的an无限趋近于一个常数A,那么A叫做数列{an}的极限,或叫做数列{an}收敛于A,记作 。
概念
数列的极限概念:
读作“n趋向于无穷大时, {an}的极限等于A”
代数式:
无穷数列
动态趋向的过程
n要多大,有多大
n不是一个有限的值
唯一的
一个常数
概念
描述{an}的变化趋势
无限多项以后
和A要多近,有多近
概念
散点图:
在n无限增大的变化过程中, {an}的点和y=A这条直线无限得近。
概念
刘徽(约公元225年—295年)
“割之弥细,所失弥少,割之又割,以至不可割,则与圆周合体,而无所失矣。”
——《九章算术》方田章圆田术刘徽注
练习
庄子(约公元前369年—约公元前286年)
“一尺之棰,日取其半,万世不竭。”
——《庄子 天下篇》
练习
“一尺之棰,日取其半,万世不竭。”
练习
练习
常用极限:
练习
代数:
推广:
特殊:
反例:
练习
{7DF18680-E054-41AD-8BC1-D1AEF772440D}
0.1
3
<0.0625
成立
0.01
6
<0.0078125
成立
0.001
9
<0.0009765625
成立
0.0001
13
<0.00006103515625
成立
0.00001
16
<0.000001525878906
成立
成立
练习:判断下列数列的极限是否存在,
若存在,极限为多少?
练习
练习7.7(1),7.7(2)
1、能不能定量地描述数列的极限?
2、数列的极限能否进行四则运算?
3、了解数列的极限在生活中的应用
4、了解数列的极限发展的数学史
回家作业:
思考:
