沪教版(上海)数学高二上册-7.1 数列(1) 课件(23张PPT)
文档属性
| 名称 | 沪教版(上海)数学高二上册-7.1 数列(1) 课件(23张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 270.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 20:22:14 | ||
图片预览







文档简介
7.1.1 数列(1)
目标与要求
教学目标
学习要求
知识与技能:
1.通过问题情境的导入,了解数列的概念和几种表示(列表、图象、通项公式);
2.掌握数列的通项公式、递推公式。
过程与方法:
教学生学会观察、分析、归纳、猜想、概括数列规律,学会用函数的方法来研究数列性质。
情感态度与价值观:
让学生感受数列是反映自然规律、来源于生活实际的基本数学模型。
〔教学目标〕
〔学习要求 〕
1.通过问题情境的导入,了解数列的概念和几种表示(列表、图象、通项公式);
2.掌握数列的通项公式、递推公式。
3.教学生学会观察、分析、归纳、猜想、概括数列规律,学会用函数的方法来研究数列性质。
4.让学生感受数列是反映自然规律、来源于生活实际的基本数学模型。
准备导入
导入一
导入二
导入三
导入四
〔准备与导入一〕
(X-1)
古希腊毕达哥拉斯学派的数学家在公元前已研究过三角形数:1,3,6,10,…和正方形数(平方数):1,4,9,16,…
问题情境一:
思考:
你能写出后面的数吗?
再比如:自然数顺序排列:0,1,2,3,4,…
1.这种按一定次序排列起来的一列数叫做数列;
2.数列中的每一个数叫做数列的项;
3.数列的一般形式可以写成: ,其中 是
数列的第n项,n是 的序数以上数列可以简单记作
〔准备与导入二〕
(X-1)
问题情境二:
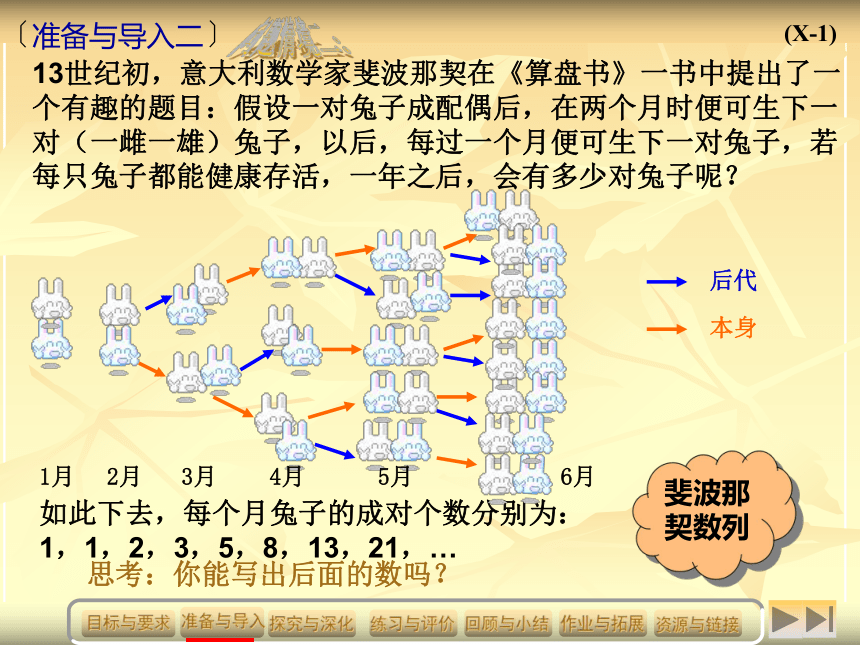
13世纪初,意大利数学家斐波那契在《算盘书》一书中提出了一个有趣的题目:假设一对兔子成配偶后,在两个月时便可生下一对(一雌一雄)兔子,以后,每过一个月便可生下一对兔子,若每只兔子都能健康存活,一年之后,会有多少对兔子呢?
如此下去,每个月兔子的成对个数分别为:1,1,2,3,5,8,13,21,…
思考:你能写出后面的数吗?
斐波那契数列
1月
2月
3月
4月
5月
6月
后代
本身
〔准备与导入三〕
(X-1)
思考:
你还能列举一些数列的例子吗?
答:
生活中有哪些数列的例子?
思考:
(1)某人到银行存款1万元,存期一年,年利率3.6%,到期 自动转存,如此连存五年后取出,那么每年的利息组成的数列为:
(2)如国际象棋的发明人达依乐的麦粒个数组成的数列:1,2,4,8,16,32,……
思考
以上列举的数列如何进行分类?
〔准备与导入四〕
(X-1)
数列的分类:
1.按数列的项分类:
2.按数列每一项的大小分类:
有穷数列
无穷数列
递增数列
递减数列
常数列
摆动数列
思考
上面的各类数列如何表示?
通项公式定义
如果数列 的第n项 与项的序数n之间的关系可以用一个公式来表示,则这个公式就叫做这个数列的通项公式(general term)
从函数的角度看,数列可以看成是以N*(或其有限子集)为定义域的函数 ,当自变量n按从小到大顺序取值时, 所对应的一列数。
想一想
探究与深化
探究一
探究二
〔探究与深化一〕
(X-1)
分析:
在通项公式依次取n=1,2,3,4得到数列的前4项
解:
〔探究与深化二〕
(X-1)
……
分析:
第一幅图中:1列2行
第二幅图中:2列3行
第n幅图中:n列n+1行
…
…
所以,函数的通项公式为
练习与评价
练习一
练习二
练习三
〔练习与评价一〕
(X-1)
解:
(1)
(2)
设:420是此函数的第k项
则k(k+1)=420
∵k为自然数
∴k=20
可知,420是数列的第20项
〔练习与评价二〕
(X-1)
分析:
第(1)图中:1个点
第(2)图中:1+2×1个点
第(3)图中:1+3×2个点
第(4)图中:1+4×3个点
因此,推得第n个图中有1+n(n-1)个点
〔练习与评价三〕
(X-1)
解:
回顾与小结
〔回顾与小结〕
(X-1)
1.本节主要让学生掌握数列的概念的 归纳形式,探索数列的分类及表示方法——通项公式
2.让学生学会用联系的方法,把数列作为一种特殊的函数来研究进一步深化数列的本质
作业与拓展
〔作业与拓展一〕
(X-1)
布置作业:
课本P7 练习7.1(1)
练习册7.1A组1-8
(X-1)
〔作业与拓展二〕
我来试一试
思考:
根据前若干项归纳得出的通项公式一定是唯一的吗?
回答:不一定。
提问:比如(4)你能写出它另外的通项公式吗?
回答:
拓展思考:是不是所有的数列都有通项公式呢?举例说明。
资源与链接
[资源与链接]
(X-1)
目标与要求
教学目标
学习要求
知识与技能:
1.通过问题情境的导入,了解数列的概念和几种表示(列表、图象、通项公式);
2.掌握数列的通项公式、递推公式。
过程与方法:
教学生学会观察、分析、归纳、猜想、概括数列规律,学会用函数的方法来研究数列性质。
情感态度与价值观:
让学生感受数列是反映自然规律、来源于生活实际的基本数学模型。
〔教学目标〕
〔学习要求 〕
1.通过问题情境的导入,了解数列的概念和几种表示(列表、图象、通项公式);
2.掌握数列的通项公式、递推公式。
3.教学生学会观察、分析、归纳、猜想、概括数列规律,学会用函数的方法来研究数列性质。
4.让学生感受数列是反映自然规律、来源于生活实际的基本数学模型。
准备导入
导入一
导入二
导入三
导入四
〔准备与导入一〕
(X-1)
古希腊毕达哥拉斯学派的数学家在公元前已研究过三角形数:1,3,6,10,…和正方形数(平方数):1,4,9,16,…
问题情境一:
思考:
你能写出后面的数吗?
再比如:自然数顺序排列:0,1,2,3,4,…
1.这种按一定次序排列起来的一列数叫做数列;
2.数列中的每一个数叫做数列的项;
3.数列的一般形式可以写成: ,其中 是
数列的第n项,n是 的序数以上数列可以简单记作
〔准备与导入二〕
(X-1)
问题情境二:
13世纪初,意大利数学家斐波那契在《算盘书》一书中提出了一个有趣的题目:假设一对兔子成配偶后,在两个月时便可生下一对(一雌一雄)兔子,以后,每过一个月便可生下一对兔子,若每只兔子都能健康存活,一年之后,会有多少对兔子呢?
如此下去,每个月兔子的成对个数分别为:1,1,2,3,5,8,13,21,…
思考:你能写出后面的数吗?
斐波那契数列
1月
2月
3月
4月
5月
6月
后代
本身
〔准备与导入三〕
(X-1)
思考:
你还能列举一些数列的例子吗?
答:
生活中有哪些数列的例子?
思考:
(1)某人到银行存款1万元,存期一年,年利率3.6%,到期 自动转存,如此连存五年后取出,那么每年的利息组成的数列为:
(2)如国际象棋的发明人达依乐的麦粒个数组成的数列:1,2,4,8,16,32,……
思考
以上列举的数列如何进行分类?
〔准备与导入四〕
(X-1)
数列的分类:
1.按数列的项分类:
2.按数列每一项的大小分类:
有穷数列
无穷数列
递增数列
递减数列
常数列
摆动数列
思考
上面的各类数列如何表示?
通项公式定义
如果数列 的第n项 与项的序数n之间的关系可以用一个公式来表示,则这个公式就叫做这个数列的通项公式(general term)
从函数的角度看,数列可以看成是以N*(或其有限子集)为定义域的函数 ,当自变量n按从小到大顺序取值时, 所对应的一列数。
想一想
探究与深化
探究一
探究二
〔探究与深化一〕
(X-1)
分析:
在通项公式依次取n=1,2,3,4得到数列的前4项
解:
〔探究与深化二〕
(X-1)
……
分析:
第一幅图中:1列2行
第二幅图中:2列3行
第n幅图中:n列n+1行
…
…
所以,函数的通项公式为
练习与评价
练习一
练习二
练习三
〔练习与评价一〕
(X-1)
解:
(1)
(2)
设:420是此函数的第k项
则k(k+1)=420
∵k为自然数
∴k=20
可知,420是数列的第20项
〔练习与评价二〕
(X-1)
分析:
第(1)图中:1个点
第(2)图中:1+2×1个点
第(3)图中:1+3×2个点
第(4)图中:1+4×3个点
因此,推得第n个图中有1+n(n-1)个点
〔练习与评价三〕
(X-1)
解:
回顾与小结
〔回顾与小结〕
(X-1)
1.本节主要让学生掌握数列的概念的 归纳形式,探索数列的分类及表示方法——通项公式
2.让学生学会用联系的方法,把数列作为一种特殊的函数来研究进一步深化数列的本质
作业与拓展
〔作业与拓展一〕
(X-1)
布置作业:
课本P7 练习7.1(1)
练习册7.1A组1-8
(X-1)
〔作业与拓展二〕
我来试一试
思考:
根据前若干项归纳得出的通项公式一定是唯一的吗?
回答:不一定。
提问:比如(4)你能写出它另外的通项公式吗?
回答:
拓展思考:是不是所有的数列都有通项公式呢?举例说明。
资源与链接
[资源与链接]
(X-1)
