沪教版(上海)数学高二上册-7.7 极限概念与数列的极限 课件(20张PPT)
文档属性
| 名称 | 沪教版(上海)数学高二上册-7.7 极限概念与数列的极限 课件(20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 763.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 20:26:19 | ||
图片预览


文档简介
极限概念与数列的极限
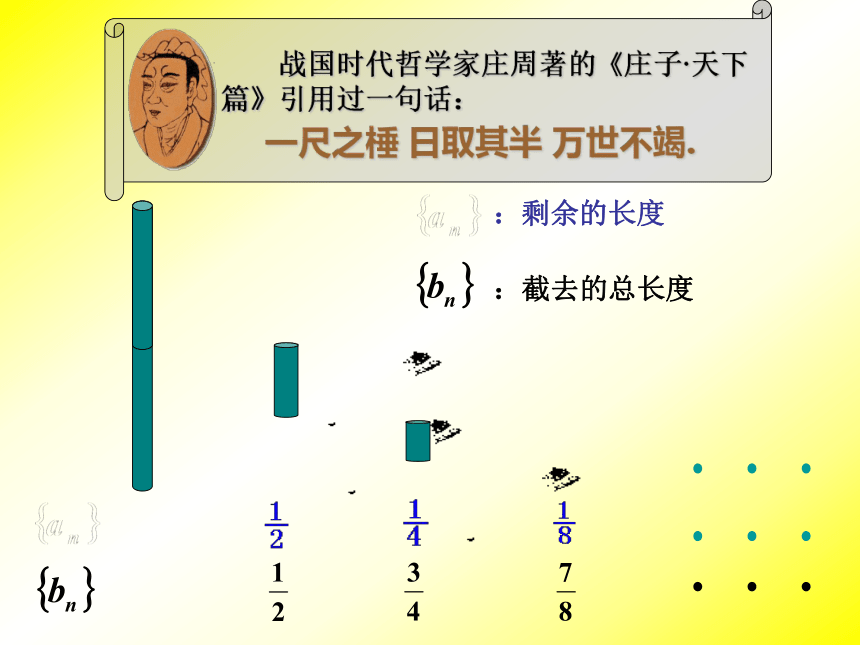
战国时代哲学家庄周著的《庄子·天下篇》引用过一句话:
一尺之棰 日取其半 万世不竭.
:剩余的长度
:截去的总长度
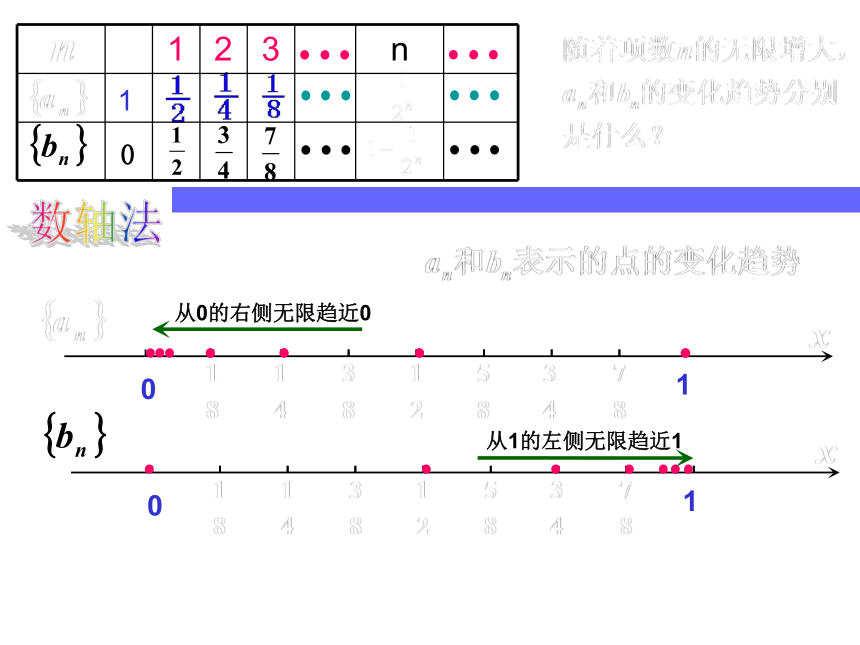
数轴法
0
1
1
0
1
2
3
n
从1的左侧无限趋近1
0
1
从0的右侧无限趋近0
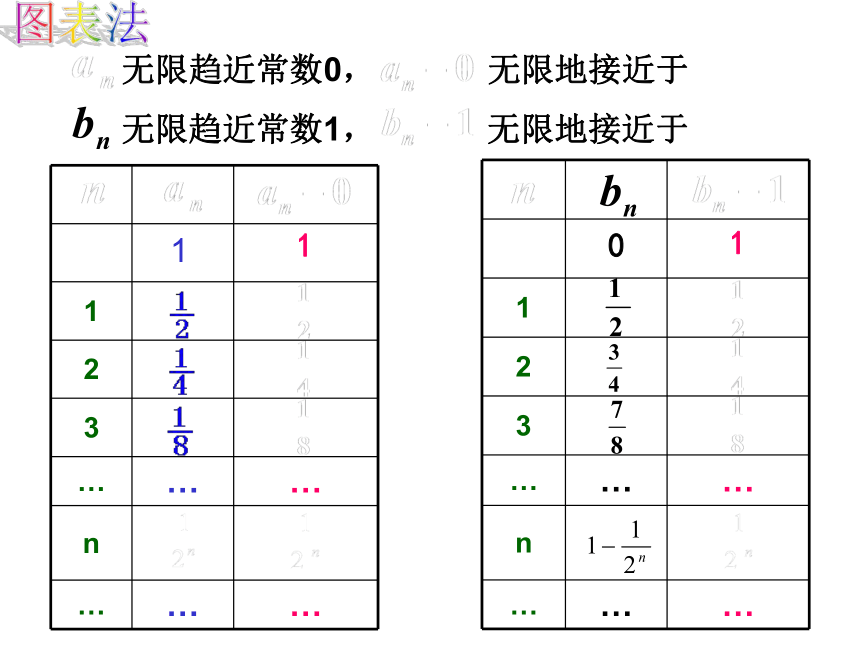
图表法
1
2
3
…
…
…
n
…
…
…
1
2
3
…
…
…
n
…
…
…
1
0
1
无限趋近常数0, 无限地接近于0
无限趋近常数1, 无限地接近于0
1
0
-1
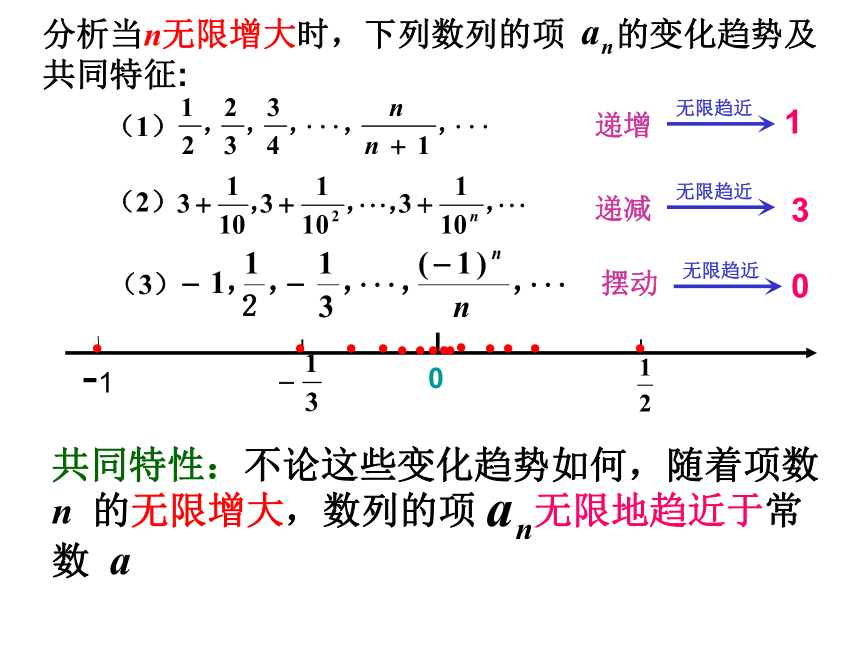
(1)
(2)
(3)
分析当n无限增大时,下列数列的项 的变化趋势及共同特征:
.
.
.
.
.
.
.
.
.
.
.
.
.
.
共同特性:不论这些变化趋势如何,随着项数 n 的无限增大,数列的项 无限地趋近于常数 a
3
递减
无限趋近
1
递增
无限趋近
0
无限趋近
摆动
n 趋向于无穷大
数列极限的描述性定义
一般地,如果当项数 无限增大时,无穷数列
的项 无限地趋近于某个常数 ,(即 无限地接近0),
那么就说数列 以 为极限,或者说
是数列 的极限
注意点
(1) 是无穷数列
(2) 无限增大时, 不是一般地趋近于 ,而是
“无限”地趋近于
(3)数值变化趋势:递减的、递增的、摆动的
读作 “当n 趋向于无穷大时,
的极限等于a ”
或 “limit 当n 趋向于
无穷大时等于a ”
1
x
2
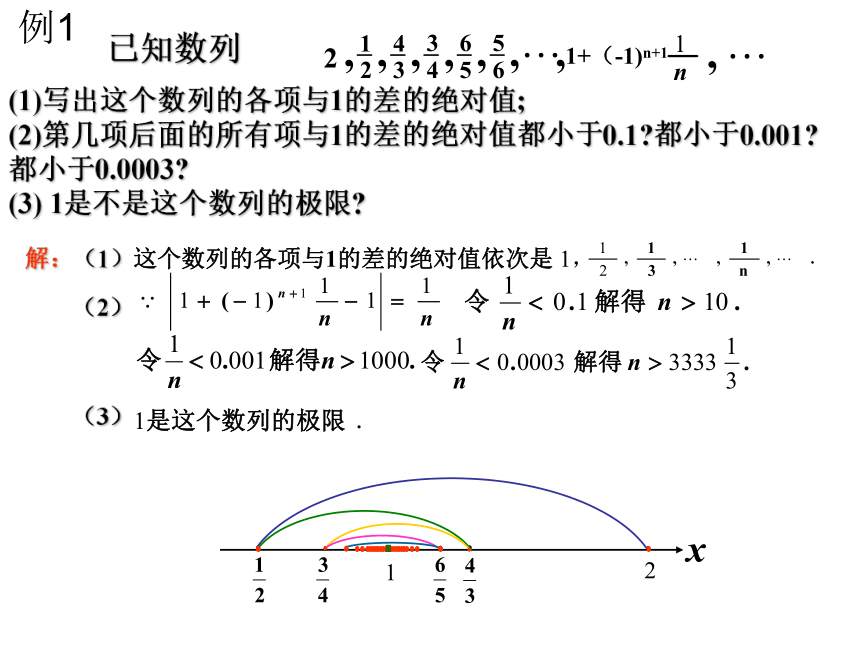
已知数列
2
1+(-1)n+1
(1)写出这个数列的各项与1的差的绝对值; (2)第几项后面的所有项与1的差的绝对值都小于0.1?都小于0.001? 都小于0.0003? (3) 1是不是这个数列的极限?
解:(1)这个数列的各项与1的差的绝对值依次是 1,
(2)
(3)
.
例1
1
x
2
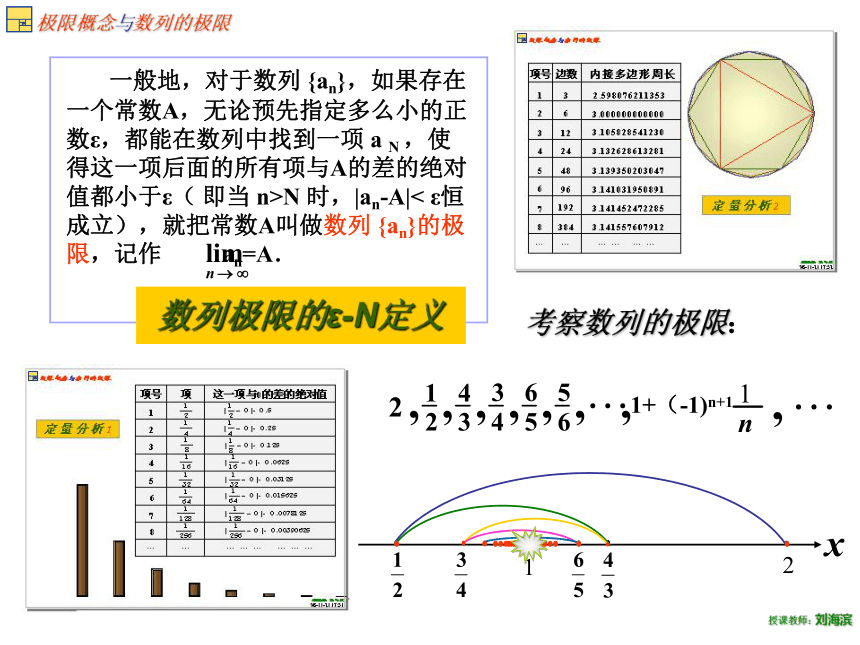
数列极限的ε-N定义
极限概念与数列的极限
授课教师:刘海滨
一般地,对于数列 {an},如果存在一个常数A,无论预先指定多么小的正数ε,都能在数列中找到一项 a N ,使得这一项后面的所有项与A的差的绝对值都小于ε( 即当 n>N 时,|an-A|< ε恒成立),就把常数A叫做数列 {an}的极限,记作 an=A.
考察数列的极限:
2
1+(-1)n+1
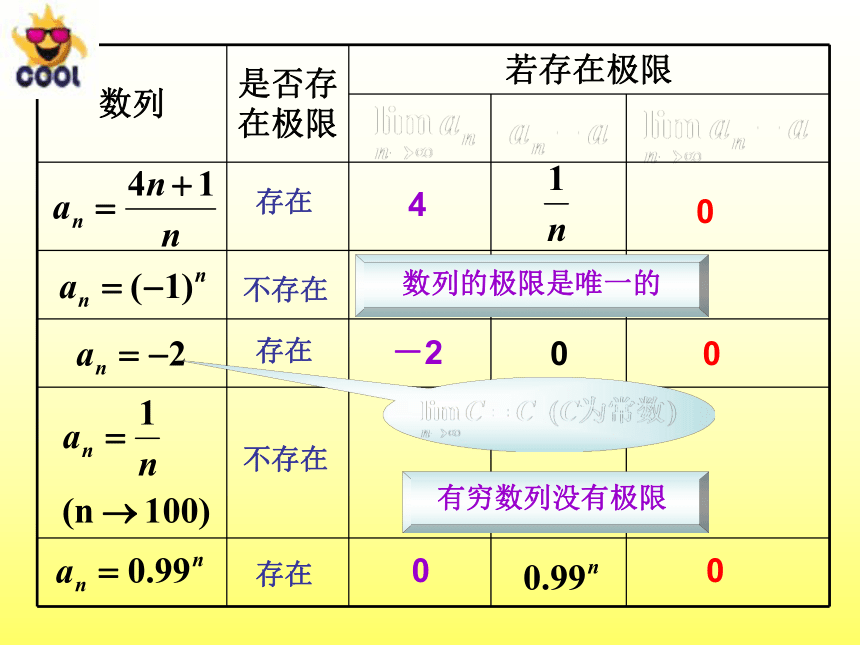
数列
是否存在极限
若存在极限
存在
不存在
存在
存在
不存在
4
0
0
0
-2
0
数列的极限是唯一的
有穷数列没有极限
0
数列
是否存在极限
若存在极限
猜想
如果 ,那么
0
存在
存在
存在
存在
不存在
5
0
0
0
“无限”地趋近于一个常数
0
0
0
0
常用数列的极限
0
对于无穷数列{an},如果当n无限增大时,an无限趋向于某一个常数a,则称a是数列{ an }的极限。
问题1:数列an = n2有极限吗?
问题2:数列
有极限吗?
问题3:数列
有极限吗?
没有
没有
有,为0
2、给出下列命题:
(1)有穷数列没有极限;
(2)无穷数列不一定有极限;
(3)无穷递减数列一定有数列;
(4)无穷递增数列一定没有数列;
(5)左右摆动的数列一定没有极限。
其中是真命题的序号有
(1)、(2)
3.请列出3个以2为极限的数列.
A.
B.
C.
D.
x
0
y
y
1、总体密度曲线
设想样本容量无限增大,分组的组距无限缩小,那么频率分布直方图就会无限接近于一条光滑曲线——总体密度曲线
数列极限思想的运用
割 圆 求 周
三国时的刘徽提出的 “割圆求周”的方法.他把圆周分成三等分、六等分、十二等分、二十四等分、··· 这样继续分割下去,所得多边形的周长就无限接近于圆的周长.
割之弥细,
所失弥少,割
之又割,以至
于不可割,则
与圆合体而无
所失矣.
小结:
1、数列极限的直观描述性定义
2、利用定义求数列极限
4、常用数列的极限
常用数列的极限
0
3、不是任何数列都有极限,但如果有极限,则极限是唯一的
练习和思考:
1、若 ,则下面几个结论中,正确的是( )
A.
B.
C.
D.
1
不存在
3:判断下列数列哪些有极限?
如果有的话,极限等于多少?如果没有,说说你的理由。
1
2
3
4
5
6
7
8
…
项号
边数
内接多边形周长
定 量 分 析
圆的半径
24
12
6
3
2.598076211353
3.000000000000
3.105828541230
3.132628613281
48
3.139350203047
96
3.141031950891
192
3.141452472285
384
3.141557607912
…
… … … …
割 圆 求 周
战国时代哲学家庄周著的《庄子·天下篇》引用过一句话:
一尺之棰 日取其半 万世不竭.
:剩余的长度
:截去的总长度
数轴法
0
1
1
0
1
2
3
n
从1的左侧无限趋近1
0
1
从0的右侧无限趋近0
图表法
1
2
3
…
…
…
n
…
…
…
1
2
3
…
…
…
n
…
…
…
1
0
1
无限趋近常数0, 无限地接近于0
无限趋近常数1, 无限地接近于0
1
0
-1
(1)
(2)
(3)
分析当n无限增大时,下列数列的项 的变化趋势及共同特征:
.
.
.
.
.
.
.
.
.
.
.
.
.
.
共同特性:不论这些变化趋势如何,随着项数 n 的无限增大,数列的项 无限地趋近于常数 a
3
递减
无限趋近
1
递增
无限趋近
0
无限趋近
摆动
n 趋向于无穷大
数列极限的描述性定义
一般地,如果当项数 无限增大时,无穷数列
的项 无限地趋近于某个常数 ,(即 无限地接近0),
那么就说数列 以 为极限,或者说
是数列 的极限
注意点
(1) 是无穷数列
(2) 无限增大时, 不是一般地趋近于 ,而是
“无限”地趋近于
(3)数值变化趋势:递减的、递增的、摆动的
读作 “当n 趋向于无穷大时,
的极限等于a ”
或 “limit 当n 趋向于
无穷大时等于a ”
1
x
2
已知数列
2
1+(-1)n+1
(1)写出这个数列的各项与1的差的绝对值; (2)第几项后面的所有项与1的差的绝对值都小于0.1?都小于0.001? 都小于0.0003? (3) 1是不是这个数列的极限?
解:(1)这个数列的各项与1的差的绝对值依次是 1,
(2)
(3)
.
例1
1
x
2
数列极限的ε-N定义
极限概念与数列的极限
授课教师:刘海滨
一般地,对于数列 {an},如果存在一个常数A,无论预先指定多么小的正数ε,都能在数列中找到一项 a N ,使得这一项后面的所有项与A的差的绝对值都小于ε( 即当 n>N 时,|an-A|< ε恒成立),就把常数A叫做数列 {an}的极限,记作 an=A.
考察数列的极限:
2
1+(-1)n+1
数列
是否存在极限
若存在极限
存在
不存在
存在
存在
不存在
4
0
0
0
-2
0
数列的极限是唯一的
有穷数列没有极限
0
数列
是否存在极限
若存在极限
猜想
如果 ,那么
0
存在
存在
存在
存在
不存在
5
0
0
0
“无限”地趋近于一个常数
0
0
0
0
常用数列的极限
0
对于无穷数列{an},如果当n无限增大时,an无限趋向于某一个常数a,则称a是数列{ an }的极限。
问题1:数列an = n2有极限吗?
问题2:数列
有极限吗?
问题3:数列
有极限吗?
没有
没有
有,为0
2、给出下列命题:
(1)有穷数列没有极限;
(2)无穷数列不一定有极限;
(3)无穷递减数列一定有数列;
(4)无穷递增数列一定没有数列;
(5)左右摆动的数列一定没有极限。
其中是真命题的序号有
(1)、(2)
3.请列出3个以2为极限的数列.
A.
B.
C.
D.
x
0
y
y
1、总体密度曲线
设想样本容量无限增大,分组的组距无限缩小,那么频率分布直方图就会无限接近于一条光滑曲线——总体密度曲线
数列极限思想的运用
割 圆 求 周
三国时的刘徽提出的 “割圆求周”的方法.他把圆周分成三等分、六等分、十二等分、二十四等分、··· 这样继续分割下去,所得多边形的周长就无限接近于圆的周长.
割之弥细,
所失弥少,割
之又割,以至
于不可割,则
与圆合体而无
所失矣.
小结:
1、数列极限的直观描述性定义
2、利用定义求数列极限
4、常用数列的极限
常用数列的极限
0
3、不是任何数列都有极限,但如果有极限,则极限是唯一的
练习和思考:
1、若 ,则下面几个结论中,正确的是( )
A.
B.
C.
D.
1
不存在
3:判断下列数列哪些有极限?
如果有的话,极限等于多少?如果没有,说说你的理由。
1
2
3
4
5
6
7
8
…
项号
边数
内接多边形周长
定 量 分 析
圆的半径
24
12
6
3
2.598076211353
3.000000000000
3.105828541230
3.132628613281
48
3.139350203047
96
3.141031950891
192
3.141452472285
384
3.141557607912
…
… … … …
割 圆 求 周
