沪教版(上海)数学高二上册-8.1 平面向量的概念 课件(16张PPT)
文档属性
| 名称 | 沪教版(上海)数学高二上册-8.1 平面向量的概念 课件(16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 273.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 20:27:08 | ||
图片预览





文档简介
课题:平面向量的概念
情景一:
南京的某一路标指示牌
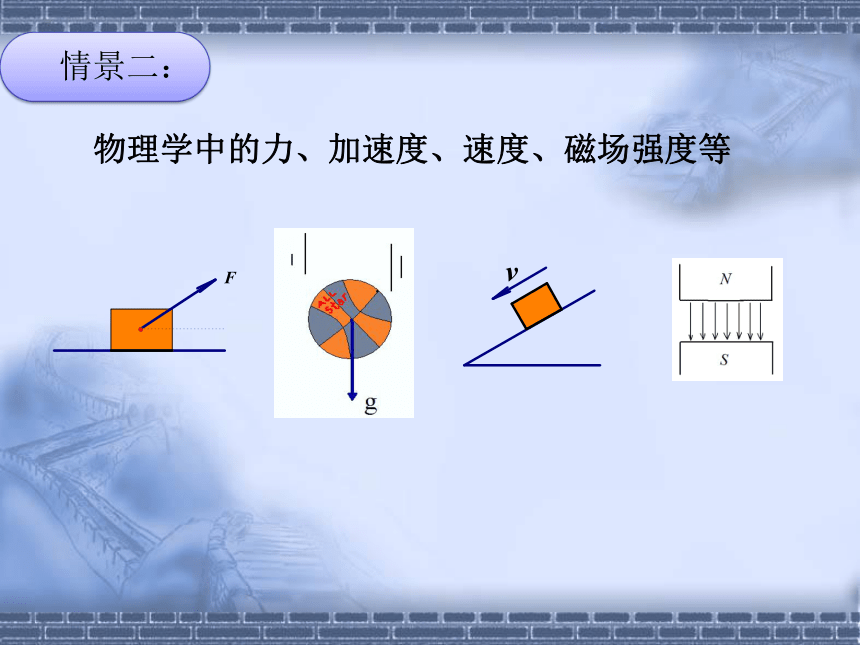
情景二:
物理学中的力、加速度、速度、磁场强度等
一、向量的定义
定义:既有大小又有方向的量叫向量。(两要素:大小、方向)
向量与数量的区别:
1.数量只有大小,是一个代数量,可以比较大小。
2.向量有大小、方向双重属性,而方向是不能比较大小的,因此向量不能比较大小。
新课讲解:
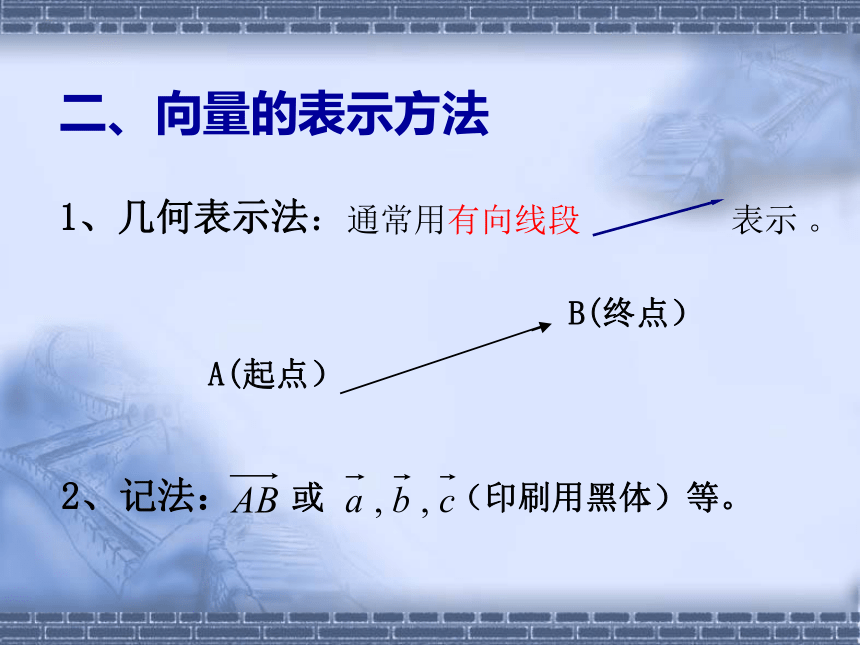
二、向量的表示方法
A(起点)
B(终点)
通常用有向线段 表示 。
1、几何表示法:
2、记法:
或 (印刷用黑体)等。
三、向量的有关概念
记作:
思考:向量不可以比较大小,向量的模可以比较大小吗?
? 向量 的大小叫做 的长度(或向量 的模)。
1、向量的长度(模):
2、两个特殊向量
(1)零向量:一般地,我们把长度为零的向量叫做零向量,
记作 。
规定: 的方向可以是任意的(或者说不确定)
(2)单位向量: 我们把模为1的向量叫做单位向量,
常用 等表示。
如图,在梯形ABCD中,AD∥BC,过A点作AE∥DC交BC于E点.
探究:
(1)相等向量:方向相同且长度相等的两个向量叫做相等的向量.
(2)相反向量(负向量):方向相反且长度相等的两个向量叫做互为相反的向量.
(3)平行向量:方向相同或相反的两个向量叫做平行向量.
3、向量间的关系
向量 与 相等,记作:
向量 与 相反,记作:
向量 与 平行,记作:
1、下列说法中不正确的是( )
A、平行向量是相等向量或相反向量 B、相反向量是平行向量
C、相等向量是平行向量 D、零向量与任意向量平行
2、设 是 的负向量,则下列说法中不正确是( )
A、 与 的长度一定相等 B、 与 是平行向量
C、 与 一定不相等 D、 一定也是 的负向量
A
C
辨析概念:
【例1】选择题
【例2】如图,设O是正六边形的中心,分别写出图中与
向量 相等向量、相反向量、平行的非零向量。
B
A
C
D
E
F
O
1、如图所示,D、E、F分别是三角形ABC各边中点,
求 的相等向量,相反向量,平行向量。
A
B
C
D
E
F
巩固概念:
2、某人从A点出发向东走了5米到达B点,然后改变方
向按东北方向走了 米到达C点,到达C点后又改变
方向向西走了10米到达D点。
(1)作出向量AB,BC,CD;
(2)求AD的模
1m
A
B
C
D
西
东
北
南
向量
定义
长度(模)
表示
几何表示法:有向线段
记法:
零向量
单位向量
向量间
的关系
相反向量(负向量)
相等向量
向量的有关概念
特殊向量
AB
a ,b
平行向量
课堂小结:
?
相等向量
相反向量
平行向量
方向
相同
相反
相同或相反
大小
相等
相等
无关
向量间的关系:
1、讲义P106练习22.7 1、2、3
2、预习平面向量的加减法
作业布置:
情景一:
南京的某一路标指示牌
情景二:
物理学中的力、加速度、速度、磁场强度等
一、向量的定义
定义:既有大小又有方向的量叫向量。(两要素:大小、方向)
向量与数量的区别:
1.数量只有大小,是一个代数量,可以比较大小。
2.向量有大小、方向双重属性,而方向是不能比较大小的,因此向量不能比较大小。
新课讲解:
二、向量的表示方法
A(起点)
B(终点)
通常用有向线段 表示 。
1、几何表示法:
2、记法:
或 (印刷用黑体)等。
三、向量的有关概念
记作:
思考:向量不可以比较大小,向量的模可以比较大小吗?
? 向量 的大小叫做 的长度(或向量 的模)。
1、向量的长度(模):
2、两个特殊向量
(1)零向量:一般地,我们把长度为零的向量叫做零向量,
记作 。
规定: 的方向可以是任意的(或者说不确定)
(2)单位向量: 我们把模为1的向量叫做单位向量,
常用 等表示。
如图,在梯形ABCD中,AD∥BC,过A点作AE∥DC交BC于E点.
探究:
(1)相等向量:方向相同且长度相等的两个向量叫做相等的向量.
(2)相反向量(负向量):方向相反且长度相等的两个向量叫做互为相反的向量.
(3)平行向量:方向相同或相反的两个向量叫做平行向量.
3、向量间的关系
向量 与 相等,记作:
向量 与 相反,记作:
向量 与 平行,记作:
1、下列说法中不正确的是( )
A、平行向量是相等向量或相反向量 B、相反向量是平行向量
C、相等向量是平行向量 D、零向量与任意向量平行
2、设 是 的负向量,则下列说法中不正确是( )
A、 与 的长度一定相等 B、 与 是平行向量
C、 与 一定不相等 D、 一定也是 的负向量
A
C
辨析概念:
【例1】选择题
【例2】如图,设O是正六边形的中心,分别写出图中与
向量 相等向量、相反向量、平行的非零向量。
B
A
C
D
E
F
O
1、如图所示,D、E、F分别是三角形ABC各边中点,
求 的相等向量,相反向量,平行向量。
A
B
C
D
E
F
巩固概念:
2、某人从A点出发向东走了5米到达B点,然后改变方
向按东北方向走了 米到达C点,到达C点后又改变
方向向西走了10米到达D点。
(1)作出向量AB,BC,CD;
(2)求AD的模
1m
A
B
C
D
西
东
北
南
向量
定义
长度(模)
表示
几何表示法:有向线段
记法:
零向量
单位向量
向量间
的关系
相反向量(负向量)
相等向量
向量的有关概念
特殊向量
AB
a ,b
平行向量
课堂小结:
?
相等向量
相反向量
平行向量
方向
相同
相反
相同或相反
大小
相等
相等
无关
向量间的关系:
1、讲义P106练习22.7 1、2、3
2、预习平面向量的加减法
作业布置:
