沪教版(上海)数学高二上册-8.1 向量的坐标表示及其运算 课件(22张PPT)
文档属性
| 名称 | 沪教版(上海)数学高二上册-8.1 向量的坐标表示及其运算 课件(22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 342.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 20:38:33 | ||
图片预览




文档简介
8.1(1)向量的坐标表示及其运算
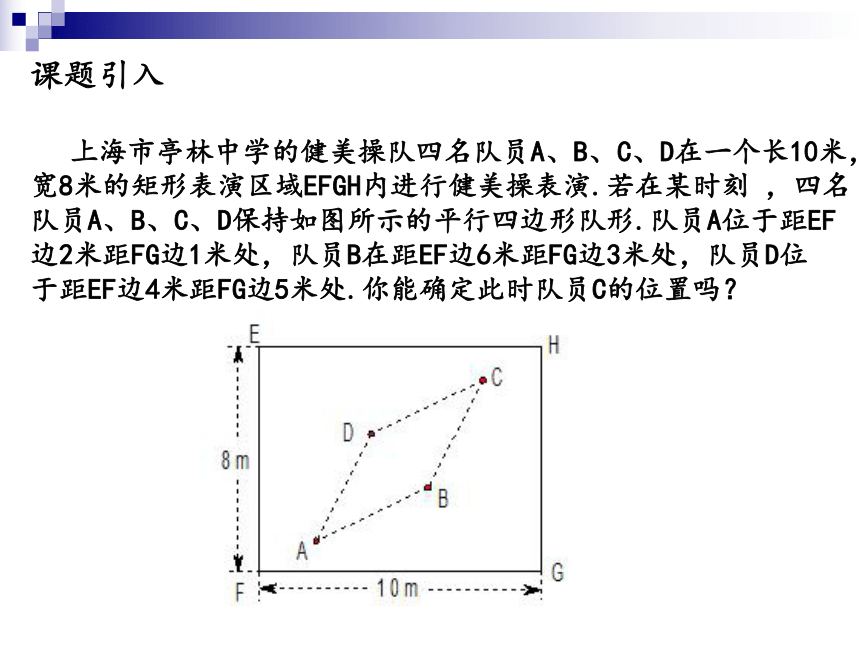
课题引入
上海市亭林中学的健美操队四名队员A、B、C、D在一个长10米,
宽8米的矩形表演区域EFGH内进行健美操表演.若在某时刻 ,四名
队员A、B、C、D保持如图所示的平行四边形队形.队员A位于距EF
边2米距FG边1米处,队员B在距EF边6米距FG边3米处,队员D位
于距EF边4米距FG边5米处.你能确定此时队员C的位置吗?
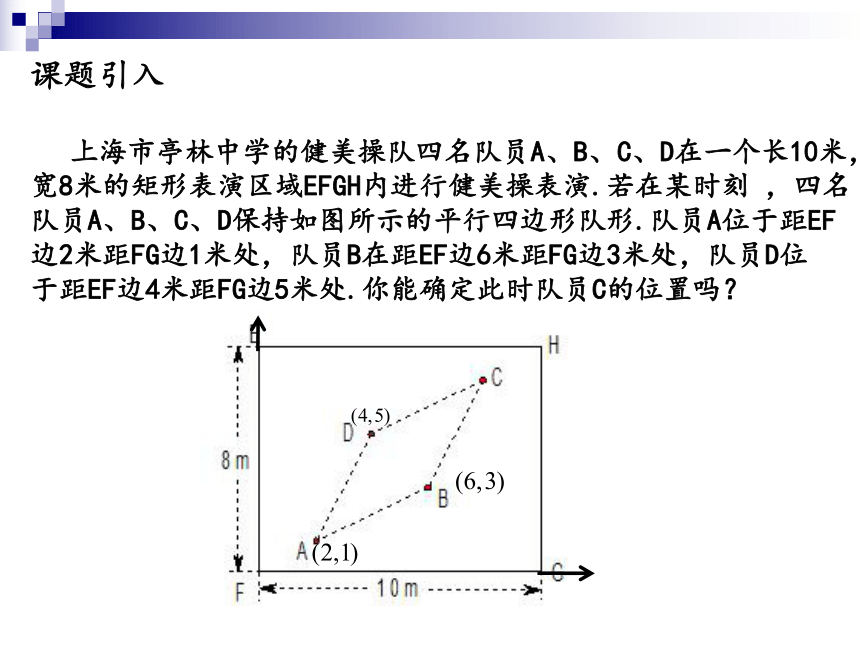
课题引入
上海市亭林中学的健美操队四名队员A、B、C、D在一个长10米,
宽8米的矩形表演区域EFGH内进行健美操表演.若在某时刻 ,四名
队员A、B、C、D保持如图所示的平行四边形队形.队员A位于距EF
边2米距FG边1米处,队员B在距EF边6米距FG边3米处,队员D位
于距EF边4米距FG边5米处.你能确定此时队员C的位置吗?
0
x
y
A
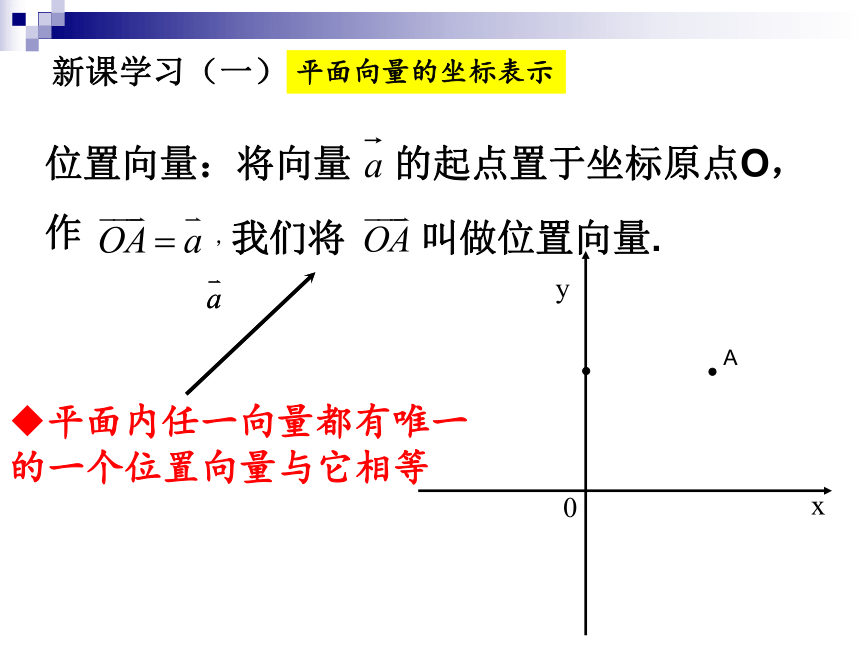
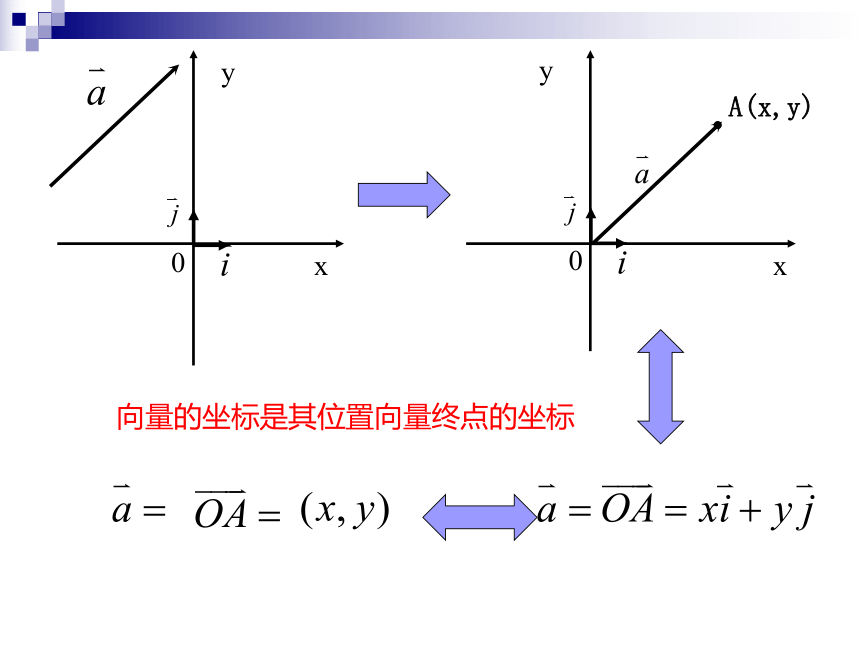
位置向量:将向量 的起点置于坐标原点O,
作 ,
我们将 叫做位置向量.
新课学习(一)
平面向量的坐标表示
平面内任一向量都有唯一的一个位置向量与它相等
0
x
y
A(x,y)
M
N
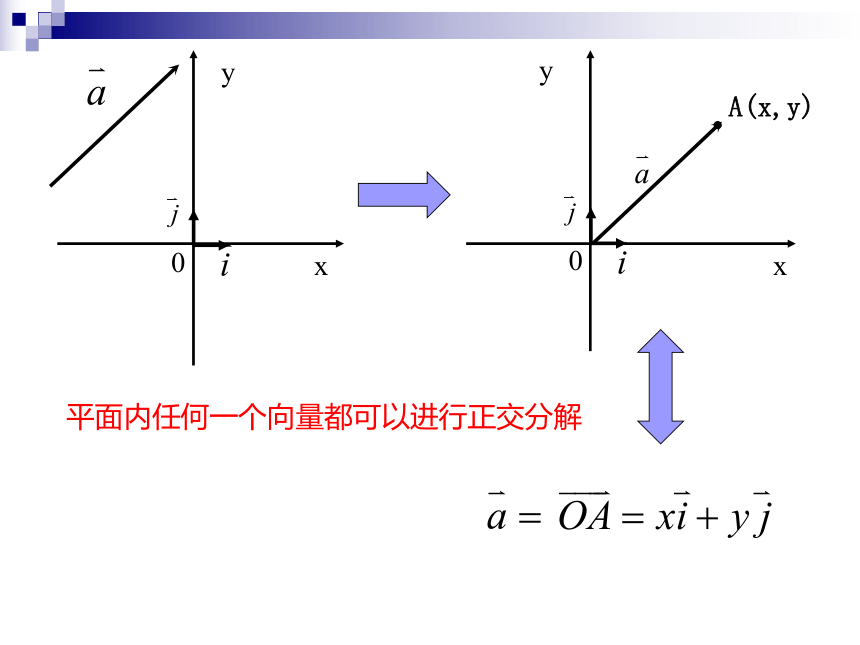
基本单位向量:在直角坐标系中,方向分别
与 轴和 轴正方向 相同的两个单位向量叫做基本单位向量.分别记作 和 .
思考:我们能用 来表示 吗?
新课学习
向量的正交分解:向量 能表示成两个互相垂直的向量 分别乘以实数 后组成的和式 ,该和式称为 的线性组合.这种向量的表示方法叫做向量的正交分解.
新课学习
0
x
y
A(x,y)
0
x
y
平面内任何一个向量都可以进行正交分解
0
x
y
A(x,y)
0
x
y
向量的坐标是其位置向量终点的坐标
任一向量
位置向量
坐标
唯一
一一对应
新课学习
问: 的坐标分别是什么?
例题分析
例1.如图,写出向量
的坐标.
新课学习(二)
平面向量的坐标运算
问4:设 为一个实数,
,那么向量 , , 的坐标分别是什么?
由于
所以
于是有:
同理有:
于是有:
新课学习
问:向量 的模能用坐标表示吗?
0
x
y
例题分析
例1.已知向量
与
,求向量
的坐标和
例题分析
思考:设
系内的任意两点,如何用P、Q的坐标来表示向量
?
是平面直角坐标
0
x
y
例3.如图,平面上
三点的坐标分别为
(1)写出向量
的坐标;
(2)如果四边形
是平行四边形,
求点 的坐标;
例题分析
D
C
(-
1
,
3
)
A
(
2
,
1
)
B
(-
3
,
2
)
y
x
O
课题引入
上海市亭林中学的健美操队四名队员A、B、C、D在一个长10米,
宽8米的矩形表演区域EFGH内进行健美操表演.若在某时刻 ,四名
队员A、B、C、D保持如图所示的平行四边形队形.队员A位于距EF
边2米距FG边1米处,队员B在距EF边6米距FG边3米处,队员D位
于距EF边4米距FG边5米处.你能确定此时队员C的位置吗?
拓展与探究
已知平面上三点的坐标分别为
D
D
D
求点D的坐标使这四点构成平行四边形
的四个顶点.
课堂小结
1.基本内容
2.思想方法
任一向量
位置向量
坐标
唯一
一一对应
谢谢!
课题引入
上海市亭林中学的健美操队四名队员A、B、C、D在一个长10米,
宽8米的矩形表演区域EFGH内进行健美操表演.若在某时刻 ,四名
队员A、B、C、D保持如图所示的平行四边形队形.队员A位于距EF
边2米距FG边1米处,队员B在距EF边6米距FG边3米处,队员D位
于距EF边4米距FG边5米处.你能确定此时队员C的位置吗?
课题引入
上海市亭林中学的健美操队四名队员A、B、C、D在一个长10米,
宽8米的矩形表演区域EFGH内进行健美操表演.若在某时刻 ,四名
队员A、B、C、D保持如图所示的平行四边形队形.队员A位于距EF
边2米距FG边1米处,队员B在距EF边6米距FG边3米处,队员D位
于距EF边4米距FG边5米处.你能确定此时队员C的位置吗?
0
x
y
A
位置向量:将向量 的起点置于坐标原点O,
作 ,
我们将 叫做位置向量.
新课学习(一)
平面向量的坐标表示
平面内任一向量都有唯一的一个位置向量与它相等
0
x
y
A(x,y)
M
N
基本单位向量:在直角坐标系中,方向分别
与 轴和 轴正方向 相同的两个单位向量叫做基本单位向量.分别记作 和 .
思考:我们能用 来表示 吗?
新课学习
向量的正交分解:向量 能表示成两个互相垂直的向量 分别乘以实数 后组成的和式 ,该和式称为 的线性组合.这种向量的表示方法叫做向量的正交分解.
新课学习
0
x
y
A(x,y)
0
x
y
平面内任何一个向量都可以进行正交分解
0
x
y
A(x,y)
0
x
y
向量的坐标是其位置向量终点的坐标
任一向量
位置向量
坐标
唯一
一一对应
新课学习
问: 的坐标分别是什么?
例题分析
例1.如图,写出向量
的坐标.
新课学习(二)
平面向量的坐标运算
问4:设 为一个实数,
,那么向量 , , 的坐标分别是什么?
由于
所以
于是有:
同理有:
于是有:
新课学习
问:向量 的模能用坐标表示吗?
0
x
y
例题分析
例1.已知向量
与
,求向量
的坐标和
例题分析
思考:设
系内的任意两点,如何用P、Q的坐标来表示向量
?
是平面直角坐标
0
x
y
例3.如图,平面上
三点的坐标分别为
(1)写出向量
的坐标;
(2)如果四边形
是平行四边形,
求点 的坐标;
例题分析
D
C
(-
1
,
3
)
A
(
2
,
1
)
B
(-
3
,
2
)
y
x
O
课题引入
上海市亭林中学的健美操队四名队员A、B、C、D在一个长10米,
宽8米的矩形表演区域EFGH内进行健美操表演.若在某时刻 ,四名
队员A、B、C、D保持如图所示的平行四边形队形.队员A位于距EF
边2米距FG边1米处,队员B在距EF边6米距FG边3米处,队员D位
于距EF边4米距FG边5米处.你能确定此时队员C的位置吗?
拓展与探究
已知平面上三点的坐标分别为
D
D
D
求点D的坐标使这四点构成平行四边形
的四个顶点.
课堂小结
1.基本内容
2.思想方法
任一向量
位置向量
坐标
唯一
一一对应
谢谢!
