沪教版(上海)数学高二上册-8.1 向量加法运算及其几何意义 课件(17张PPT)
文档属性
| 名称 | 沪教版(上海)数学高二上册-8.1 向量加法运算及其几何意义 课件(17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 299.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 00:00:00 | ||
图片预览





文档简介
向量加法运算及其
几何意义
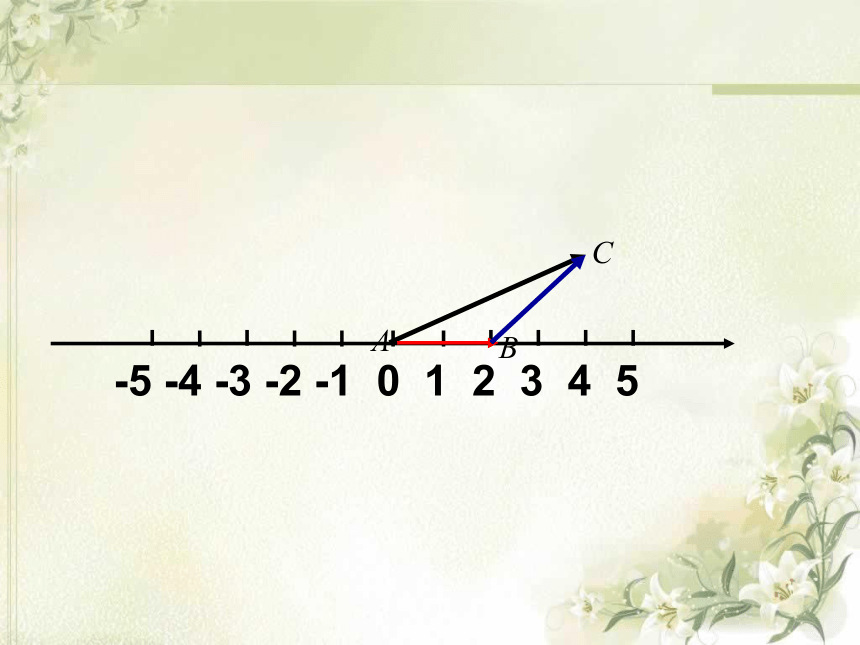
小明从原点出发,先向东走2米,再向东走了3米,相对于原点小明的最后位置在什么地方?
-5 -4 -3 -2 -1 0 1 2 3 4 5
+2
+3
(+2)+(+3)=+5
-5 -4 -3 -2 -1 0 1 2 3 4 5
求两个向量和的运算,叫做
向量的加法
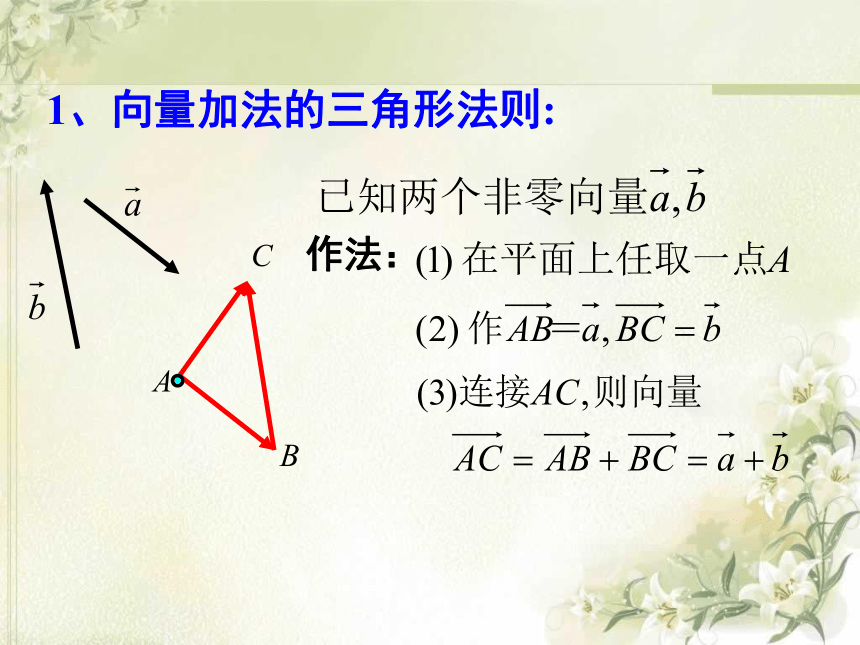
1、向量加法的三角形法则:
作法:
“首尾”顺次相接
起点指向终点
问题1:两个向量的和向量方向怎么确定?
问题2:
例1:如图,已知 ,求作向量
(1)
(2)
(3)
2、向量加法的平行四边形法则:
作法:
起点相同,两边平行
同一起点,对角为和
三角形法则与平行四边形法则,它们求
向量和的结果是否一样?
思考1:
交换律:
思考2:
向量加法是否满足结合律?并证明.
结合律:
例2:长江两岸之间没有大桥的地方,常常通过轮船进行运输,
如图所示,一艘船从长江南岸 点出发,以 km/h的速度向
垂直于对岸的方向行驶,同时江水的速度为向东 km/h.
(1)试用向量表示江水速度、船速以及船实际航行的速度;
(2)求船实际航行的速度的大小与方向(用与江水速度的夹
角来表示).
答:船实际航行速度为 km/h,方向与水的流速间的夹角为60?.
1、这节课你有哪些收获?
回顾:
2、留给你印象最深刻的是什么?
3、这节课之后,你还想做些什么探究?
课堂小结:
向量加法的定义
向量加法的运算律
三角形法则
平行四边形法则
向量加法的运算
作业:
(1)作业: P91 习题2.2的1.2.3.
(2)拓展作业: 数有减法,向量是否有减法
呢?结合本节课的探究方法,请大胆的
提出猜想,并结合三角形法则与平行四
边形法则进行探究。.
几何意义
小明从原点出发,先向东走2米,再向东走了3米,相对于原点小明的最后位置在什么地方?
-5 -4 -3 -2 -1 0 1 2 3 4 5
+2
+3
(+2)+(+3)=+5
-5 -4 -3 -2 -1 0 1 2 3 4 5
求两个向量和的运算,叫做
向量的加法
1、向量加法的三角形法则:
作法:
“首尾”顺次相接
起点指向终点
问题1:两个向量的和向量方向怎么确定?
问题2:
例1:如图,已知 ,求作向量
(1)
(2)
(3)
2、向量加法的平行四边形法则:
作法:
起点相同,两边平行
同一起点,对角为和
三角形法则与平行四边形法则,它们求
向量和的结果是否一样?
思考1:
交换律:
思考2:
向量加法是否满足结合律?并证明.
结合律:
例2:长江两岸之间没有大桥的地方,常常通过轮船进行运输,
如图所示,一艘船从长江南岸 点出发,以 km/h的速度向
垂直于对岸的方向行驶,同时江水的速度为向东 km/h.
(1)试用向量表示江水速度、船速以及船实际航行的速度;
(2)求船实际航行的速度的大小与方向(用与江水速度的夹
角来表示).
答:船实际航行速度为 km/h,方向与水的流速间的夹角为60?.
1、这节课你有哪些收获?
回顾:
2、留给你印象最深刻的是什么?
3、这节课之后,你还想做些什么探究?
课堂小结:
向量加法的定义
向量加法的运算律
三角形法则
平行四边形法则
向量加法的运算
作业:
(1)作业: P91 习题2.2的1.2.3.
(2)拓展作业: 数有减法,向量是否有减法
呢?结合本节课的探究方法,请大胆的
提出猜想,并结合三角形法则与平行四
边形法则进行探究。.
