沪教版(上海)数学高二上册-8.2 平面向量数量积的物理背景及其含义 课件(26张PPT)
文档属性
| 名称 | 沪教版(上海)数学高二上册-8.2 平面向量数量积的物理背景及其含义 课件(26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 383.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 21:05:07 | ||
图片预览






文档简介
平面向量数量积的物理背景及其含义
学习目标:
1.理解平面向量的数量积及其物理意义、几何意义;
2.掌握平面向量数量积的重要性质及运算律;
3.能够运用定义和运算性质解决相关问题.
预习提纲:
1.物理学中的功的定义是怎样的,它是标量还是矢量?
2.两个向量的夹角是如何规定的?范围是什么?
3.向量的数量积是如何定义的?如何表示?
有哪些性质?
4.如何理解投影?它是一个向量还是一个数?
看课本P103到P104
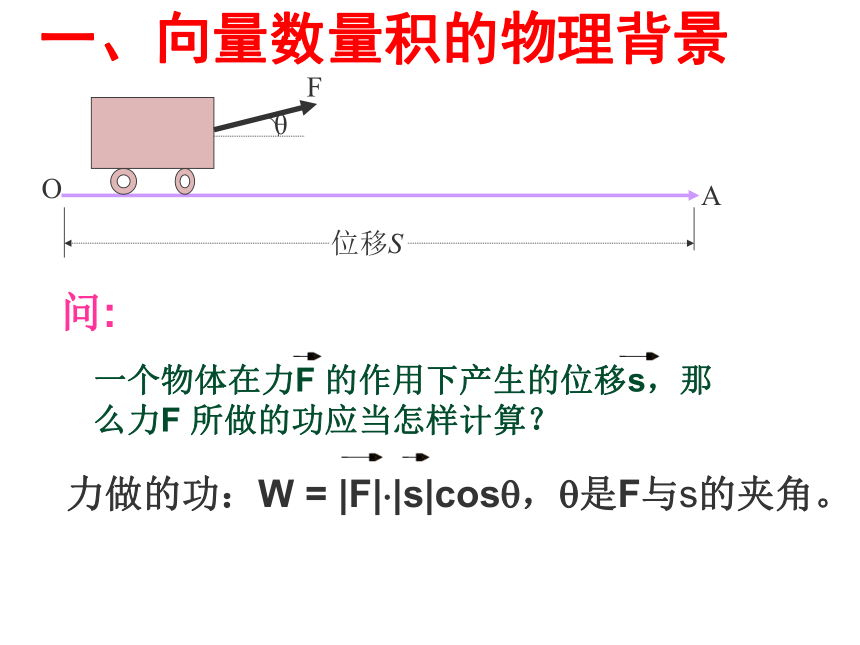
问:
一个物体在力F 的作用下产生的位移s,那么力F 所做的功应当怎样计算?
力做的功:W = |F|?|s|cos?,?是F与s的夹角。
位移S
O
A
F
θ
一、向量数量积的物理背景
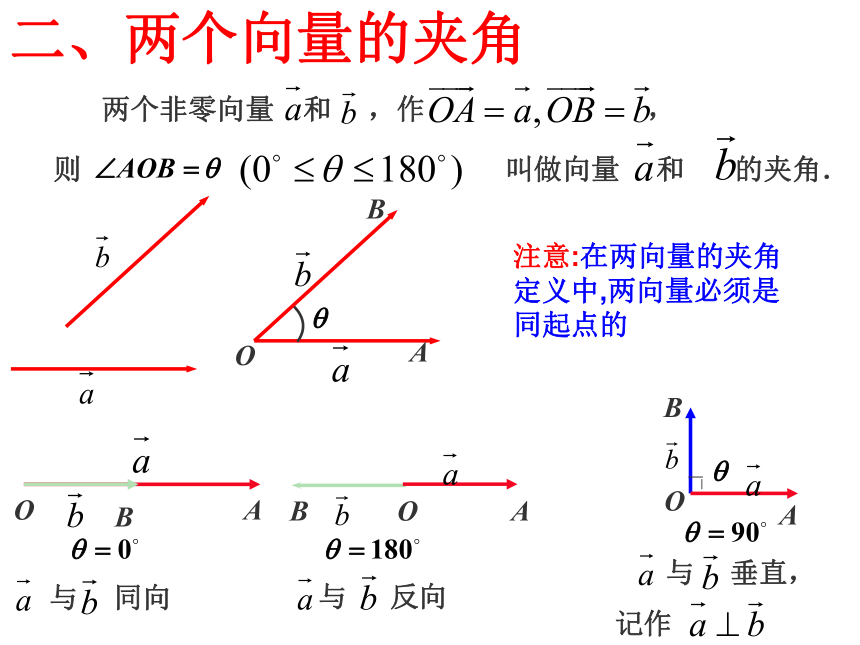
两个非零向量 和 ,作 ,
与 反向
O
A
B
O
A
与 同向
O
A
B
B
则 叫做向量 和 的夹角.
记作
与 垂直,
O
A
B
注意:在两向量的夹角定义中,两向量必须是同起点的
二、两个向量的夹角
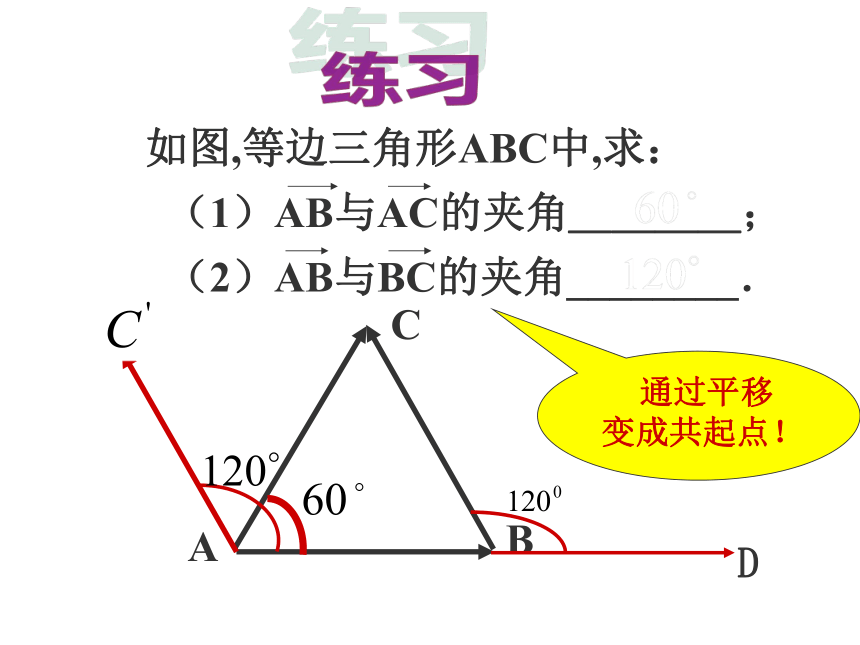
如图,等边三角形ABC中,求:
(1)AB与AC的夹角____;
(2)AB与BC的夹角________.
A
B
C
通过平移
变成共起点!
练习
D
规定:零向量与任一向量的数量积为0。
三、向量 与 的数量积的概念
注意:
数量积
a · b =| a || b |cos?
?
?
?
注意公式变形,知三求一.
?
“ · ”不能省略不写,也不能写成“×”
?
一种新的运算
向量的数量积是一个数量,那么它什么时候为正,什么时候为负?
探究:
当0°≤θ < 90°时a·b为正;
当90°<θ ≤180°时a·b为负。
当θ =90°时a·b为零。
a · b =| a || b |cos?
变式一
的夹角
与
求
,
,
,
b
a
b
a
b
a
2
8
4
|
|
4
|
|
=
·
=
=
O
A
B
b
a
?
向量数量积的
几何意义
数量积 a · b 等于a 的模| a |与 b 在 a 的方向上的投影| b |cos ?的乘积.
四、投影的概念
投影的作图:
A
O
⑤
A
O
B
| b |cos ?= ??b?
| b |cos ??0
| b |cos ??0
| b |cos ???b?
| b |cos ??0
O
A
a
B
b
θ
O
A
a
B
b
θ
O
A
a
B
b
θ
B1
B1
B
向量数量积的性质
b
a
b
a
^
?
=
·
0
)
1
(
a
a
a
a
a
a
·
=
=
·
|
|
|
|
特别地
2
或
|
||
|
)
3
(
b
a
b
a
?
·
|
||
|
|
||
|
)
2
(
b
a
b
a
b
a
b
a
b
a
b
a
-
=
·
=
·
反向时,
与
当
;
同向时,
与
当
平面向量的数量积的运算律:
其中,
是任意三个向量,
注:
O
N
M
证明运算律(3)
向量 、 、 在上的投影的数量分别是OM、MN、 ON,
则
= ON
= (OM + MN)
= OM + MN
=
例 2:求证:
例3、
的夹角为
解:
夹角的范围
运算律
性 质
数量积
(3) (a+b) ·c =
a·c+b·c
a·a=|a|2
(简写 a2 = |a|2)
重点知识回顾:
(2)
(1) a ·b= b · a
(交换律)
(分配律)
1.理解平面向量的数量积的物理意义、几何意义
2.掌握平面向量的数量积的概念
3.掌握平面向量的数量积的运算律
4.理解数量积的运算是不同于实数运算
的一种新的运算,注意它们的区别;
5.会用数量积的运算解决一些基本问题
课堂小结
检测:
是非零向量
与
1.已知:
b
a
(√)
(× )
(× )
(√)
(√)
的结果还是一个向量
b
a
·
)
1
(
(× )
2
|
|
)
2
(
a
a
a
=
·
|
||
|
|
|
)
3
(
b
a
b
a
=
·
b
a
b
a
^
?
=
·
0
)
4
(
0
)
5
(
=
·
?
^
b
a
b
a
|
||
|
//
)
6
(
b
a
b
a
b
a
=
·
?
2、判断下列说法的正误,并说明理由
错误
正确
正确
同向时,48
反向时,-48
.
8
|
|
6
|
3.|
b
a
b
a
b
a
·
=
=
求
平行,
与
,
,
作业:
学习目标:
1.理解平面向量的数量积及其物理意义、几何意义;
2.掌握平面向量数量积的重要性质及运算律;
3.能够运用定义和运算性质解决相关问题.
预习提纲:
1.物理学中的功的定义是怎样的,它是标量还是矢量?
2.两个向量的夹角是如何规定的?范围是什么?
3.向量的数量积是如何定义的?如何表示?
有哪些性质?
4.如何理解投影?它是一个向量还是一个数?
看课本P103到P104
问:
一个物体在力F 的作用下产生的位移s,那么力F 所做的功应当怎样计算?
力做的功:W = |F|?|s|cos?,?是F与s的夹角。
位移S
O
A
F
θ
一、向量数量积的物理背景
两个非零向量 和 ,作 ,
与 反向
O
A
B
O
A
与 同向
O
A
B
B
则 叫做向量 和 的夹角.
记作
与 垂直,
O
A
B
注意:在两向量的夹角定义中,两向量必须是同起点的
二、两个向量的夹角
如图,等边三角形ABC中,求:
(1)AB与AC的夹角____;
(2)AB与BC的夹角________.
A
B
C
通过平移
变成共起点!
练习
D
规定:零向量与任一向量的数量积为0。
三、向量 与 的数量积的概念
注意:
数量积
a · b =| a || b |cos?
?
?
?
注意公式变形,知三求一.
?
“ · ”不能省略不写,也不能写成“×”
?
一种新的运算
向量的数量积是一个数量,那么它什么时候为正,什么时候为负?
探究:
当0°≤θ < 90°时a·b为正;
当90°<θ ≤180°时a·b为负。
当θ =90°时a·b为零。
a · b =| a || b |cos?
变式一
的夹角
与
求
,
,
,
b
a
b
a
b
a
2
8
4
|
|
4
|
|
=
·
=
=
O
A
B
b
a
?
向量数量积的
几何意义
数量积 a · b 等于a 的模| a |与 b 在 a 的方向上的投影| b |cos ?的乘积.
四、投影的概念
投影的作图:
A
O
⑤
A
O
B
| b |cos ?= ??b?
| b |cos ??0
| b |cos ??0
| b |cos ???b?
| b |cos ??0
O
A
a
B
b
θ
O
A
a
B
b
θ
O
A
a
B
b
θ
B1
B1
B
向量数量积的性质
b
a
b
a
^
?
=
·
0
)
1
(
a
a
a
a
a
a
·
=
=
·
|
|
|
|
特别地
2
或
|
||
|
)
3
(
b
a
b
a
?
·
|
||
|
|
||
|
)
2
(
b
a
b
a
b
a
b
a
b
a
b
a
-
=
·
=
·
反向时,
与
当
;
同向时,
与
当
平面向量的数量积的运算律:
其中,
是任意三个向量,
注:
O
N
M
证明运算律(3)
向量 、 、 在上的投影的数量分别是OM、MN、 ON,
则
= ON
= (OM + MN)
= OM + MN
=
例 2:求证:
例3、
的夹角为
解:
夹角的范围
运算律
性 质
数量积
(3) (a+b) ·c =
a·c+b·c
a·a=|a|2
(简写 a2 = |a|2)
重点知识回顾:
(2)
(1) a ·b= b · a
(交换律)
(分配律)
1.理解平面向量的数量积的物理意义、几何意义
2.掌握平面向量的数量积的概念
3.掌握平面向量的数量积的运算律
4.理解数量积的运算是不同于实数运算
的一种新的运算,注意它们的区别;
5.会用数量积的运算解决一些基本问题
课堂小结
检测:
是非零向量
与
1.已知:
b
a
(√)
(× )
(× )
(√)
(√)
的结果还是一个向量
b
a
·
)
1
(
(× )
2
|
|
)
2
(
a
a
a
=
·
|
||
|
|
|
)
3
(
b
a
b
a
=
·
b
a
b
a
^
?
=
·
0
)
4
(
0
)
5
(
=
·
?
^
b
a
b
a
|
||
|
//
)
6
(
b
a
b
a
b
a
=
·
?
2、判断下列说法的正误,并说明理由
错误
正确
正确
同向时,48
反向时,-48
.
8
|
|
6
|
3.|
b
a
b
a
b
a
·
=
=
求
平行,
与
,
,
作业:
