沪教版(上海)数学高二上册-8.2 向量的数量积 课件(14张PPT)
文档属性
| 名称 | 沪教版(上海)数学高二上册-8.2 向量的数量积 课件(14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 377.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 21:19:42 | ||
图片预览




文档简介
第八章 平面向量的坐标表示
8.1.3 向量的坐标表示及其运算
8.2.1 向量的数量积
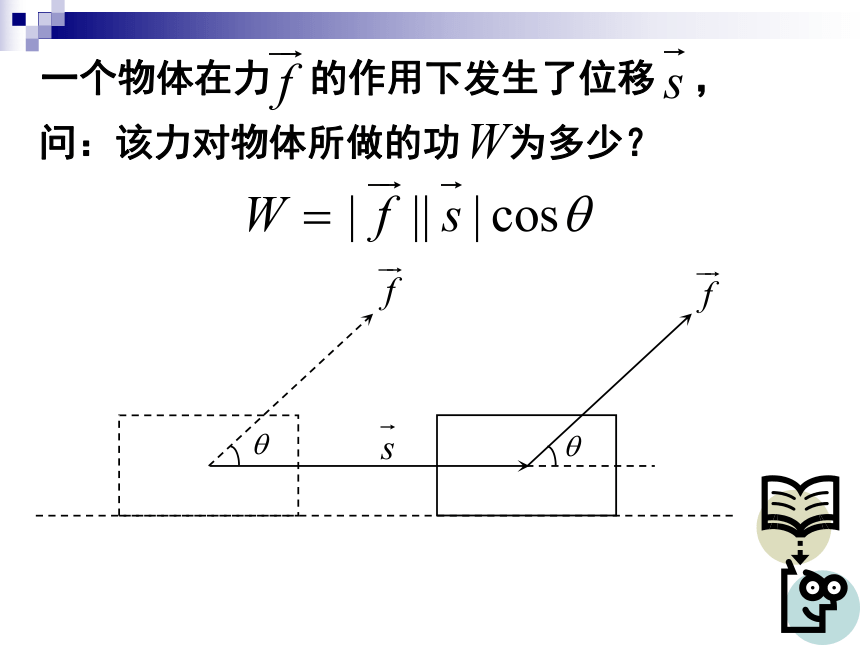
一个物体在力 的作用下发生了位移 ,
问:该力对物体所做的功 为多少?
一、向量的夹角
已知非零向量
, 作 ,
叫做向量 和向量 的夹角.
时, 同向
规定零向量与任意向量夹角根据需要确定
则
规定夹角范围:
时, 反向
时,称向量 与向量 互相垂直,
记作
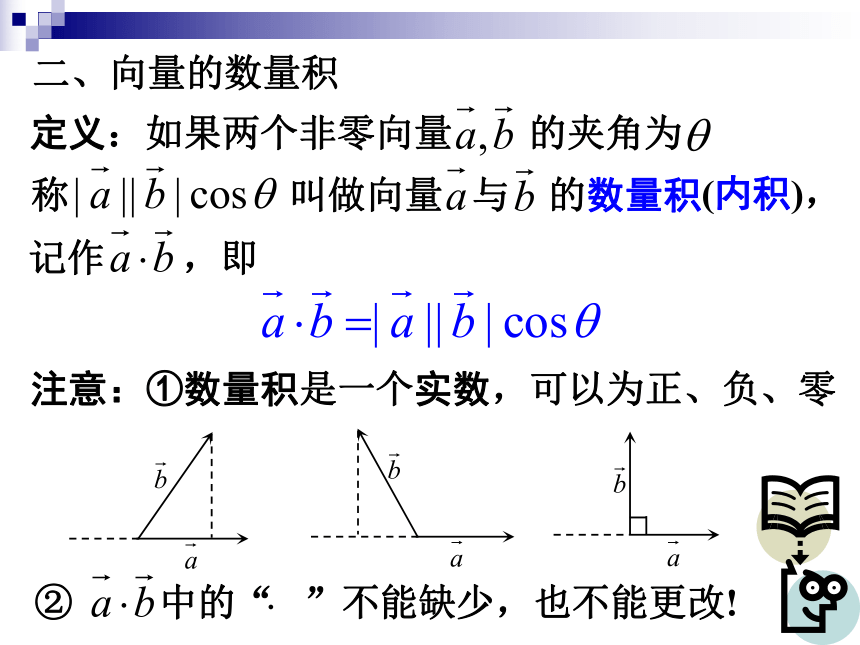
二、向量的数量积
注意:①数量积是一个实数,可以为正、负、零
定义:如果两个非零向量 的夹角为
称 叫做向量 与 的数量积
记作 ,即
② 中的“ ”不能缺少,也不能更改!
(内积),
二、向量的数量积
特别地,记 为
规定零向量与任一向量的数量积为0
思考 与 的关系是什么?
定义:如果两个非零向量 的夹角为
称 叫做向量 与 的数量积
记作 ,即
(内积),
例1.已知
(1)向量
的夹角为 ;
,按下列条件分别求
解:
(2) ;
(1)
(2)
夹角为 或
当
同向时,
当
反向时,
(3) .
(3)
夹角为
一个物体在力 的作用下发生了位移 ,
问:该力对物体所做的功 为多少?
三、向量数量积的几何含义
设 是非零向量,把 叫做向量 在
向量 方向上的投影,
它是数量.
投影>0
投影<0
投影=0
投影的正负由两个向量夹角的余弦值决定.
三、向量数量积的几何含义
的几何意义:
设 是非零向量,把 叫做向量 在
向量 方向上的投影,
它是数量.
向量 在 方向上的投影
的乘积.
数量积
思考
的几何意义是?
向量 的长度 与
例2.已知 ,
(1) 在 方向上的投影为4,求 ;
(2) ,求 在 方向上的投影;
(3) 的夹角为 ,求 在 方向上的投影.
解: (1)
(2)
(3)
思考 ,那么非零向量 应满足?
四、两个向量内积的重要性质
(1)如果 是单位向量, 则 在 方向上的投影
(2)
(3)
(4)
(5)
课堂练习
1.已知 ,求
2.已知 ,求夹角大小.
3.已知 ,求向量 在向量
方向上的投影.
4.作图证明
课堂练习答案
1.
2.
3.
4.如下图,
8.1.3 向量的坐标表示及其运算
8.2.1 向量的数量积
一个物体在力 的作用下发生了位移 ,
问:该力对物体所做的功 为多少?
一、向量的夹角
已知非零向量
, 作 ,
叫做向量 和向量 的夹角.
时, 同向
规定零向量与任意向量夹角根据需要确定
则
规定夹角范围:
时, 反向
时,称向量 与向量 互相垂直,
记作
二、向量的数量积
注意:①数量积是一个实数,可以为正、负、零
定义:如果两个非零向量 的夹角为
称 叫做向量 与 的数量积
记作 ,即
② 中的“ ”不能缺少,也不能更改!
(内积),
二、向量的数量积
特别地,记 为
规定零向量与任一向量的数量积为0
思考 与 的关系是什么?
定义:如果两个非零向量 的夹角为
称 叫做向量 与 的数量积
记作 ,即
(内积),
例1.已知
(1)向量
的夹角为 ;
,按下列条件分别求
解:
(2) ;
(1)
(2)
夹角为 或
当
同向时,
当
反向时,
(3) .
(3)
夹角为
一个物体在力 的作用下发生了位移 ,
问:该力对物体所做的功 为多少?
三、向量数量积的几何含义
设 是非零向量,把 叫做向量 在
向量 方向上的投影,
它是数量.
投影>0
投影<0
投影=0
投影的正负由两个向量夹角的余弦值决定.
三、向量数量积的几何含义
的几何意义:
设 是非零向量,把 叫做向量 在
向量 方向上的投影,
它是数量.
向量 在 方向上的投影
的乘积.
数量积
思考
的几何意义是?
向量 的长度 与
例2.已知 ,
(1) 在 方向上的投影为4,求 ;
(2) ,求 在 方向上的投影;
(3) 的夹角为 ,求 在 方向上的投影.
解: (1)
(2)
(3)
思考 ,那么非零向量 应满足?
四、两个向量内积的重要性质
(1)如果 是单位向量, 则 在 方向上的投影
(2)
(3)
(4)
(5)
课堂练习
1.已知 ,求
2.已知 ,求夹角大小.
3.已知 ,求向量 在向量
方向上的投影.
4.作图证明
课堂练习答案
1.
2.
3.
4.如下图,
