沪教版(上海)数学高二上册-8.2 向量的数量积(一) 课件(16张PPT)
文档属性
| 名称 | 沪教版(上海)数学高二上册-8.2 向量的数量积(一) 课件(16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 21:22:32 | ||
图片预览



文档简介
向量的数量积(一)
若 ,
若 ,
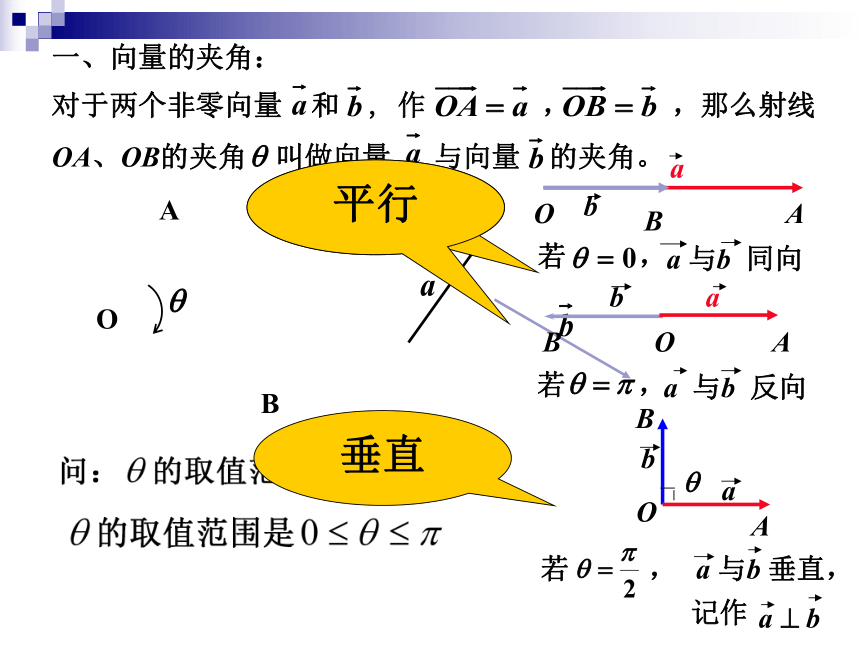
一、向量的夹角:
O
A
B
对于两个非零向量 和 , 作 , ,那么射线
OA、OB的夹角 叫做向量 与向量 的夹角。
若 ,
O
A
B
b
a
a 与b 同向
O
A
B
b
a
a 与b 反向
记作
O
A
B
a
b
a 与b 垂直,
平行
垂直
平行
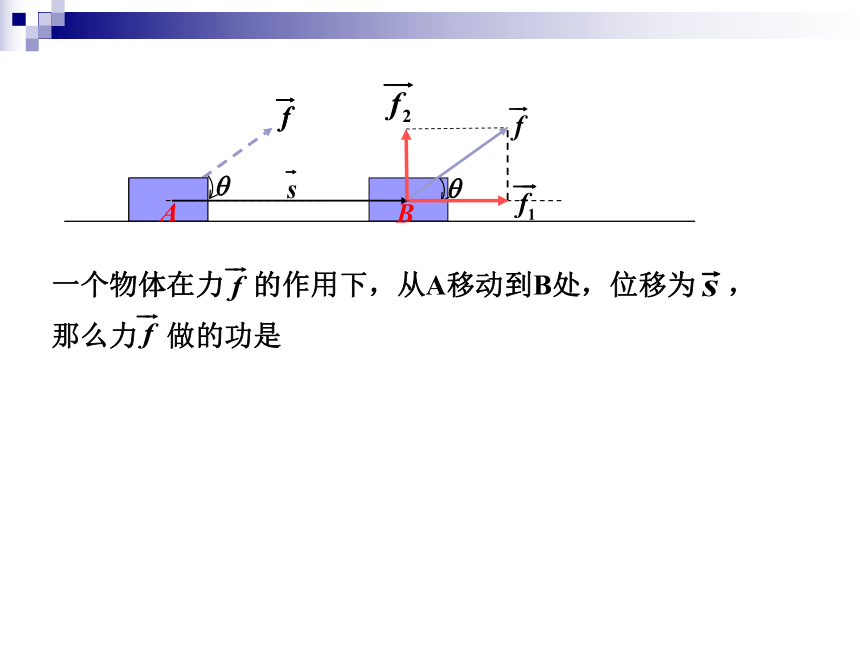
一个物体在力 的作用下,从A移动到B处,位移为 ,
那么力 做的功是
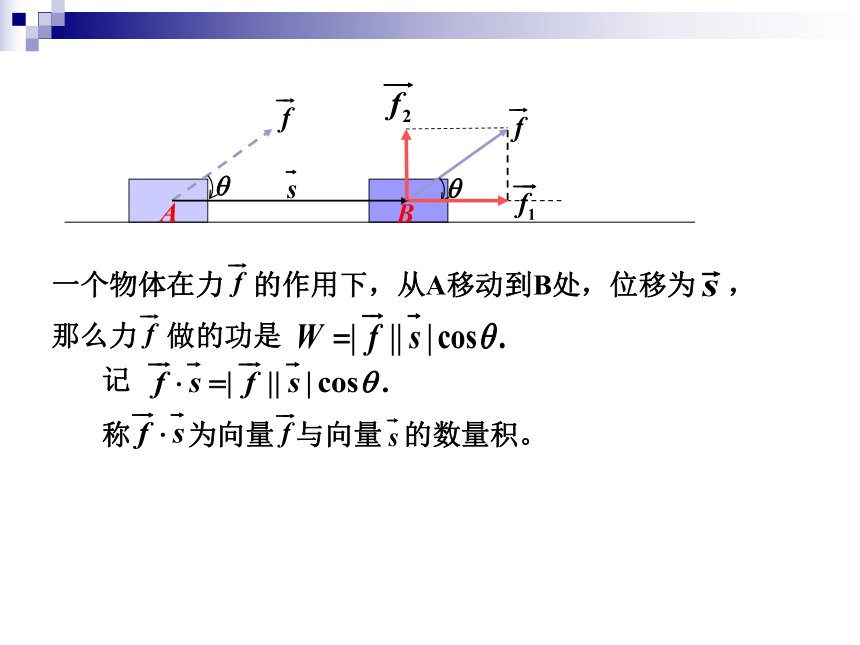
一个物体在力 的作用下,从A移动到B处,位移为 ,
那么力 做的功是
记
称 为向量 与向量 的数量积。
二、向量的数量积:
记作
一般地,两个非零向量 、 的夹角为 ,
那么我们把 叫做向量 与向量 的数量积,
即
规定:
1、两个向量的数量积是一个
2、运算符“?”
特别地,
注意:
实数
不可写为“×”,也不能省略
A
B
C
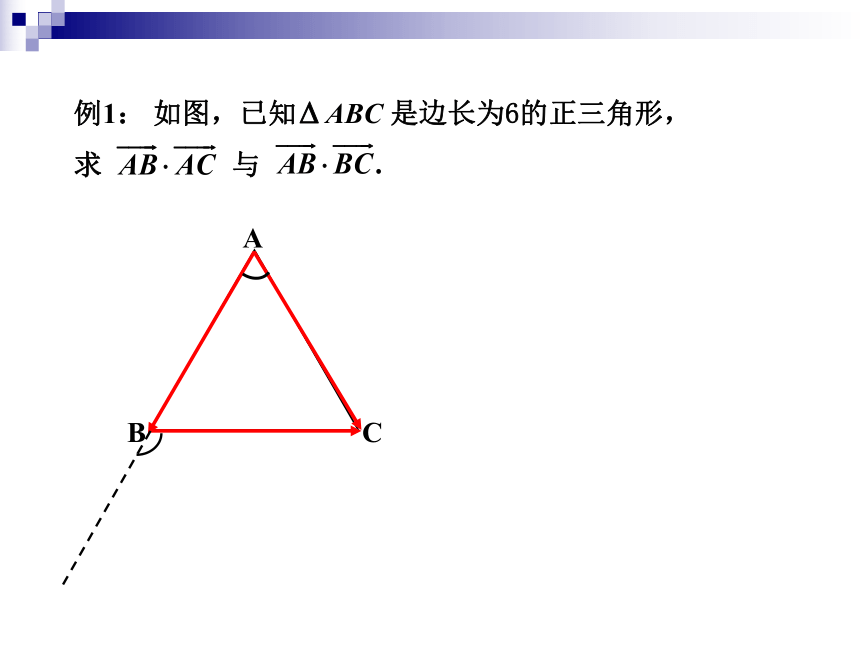
例1: 如图,已知 ABC 是边长为6的正三角形,
求 与
例2: 判断以下运算是否正确,并说明理由:
注意区分:
向量的数量积
实数与向量的乘积
实数的乘法
数量积的运算性质:
数量积的运算性质:
研究 ?
叫做向量 在向量 的方向上的投影。
数量积 的几何意义是:
两个向量 、 的数量积是其中的一个向量 的模与
另一个向量 在向量 的方向上的投影 的乘积。
| b | cosθ>0
| b | cosθ<0
| b | cosθ=0
θ为锐角时,
θ为钝角时,
O
A
B
θ为直角时,
研究
O
C
B
A
C1
B1
例3: 用 表示
例4: 已知 且 与 的夹角为
求
(1)当 时,表示向量 与向量 方向相同;
(2)当 时,表示向量 与向量 方向相反;
(3)当 时,表示向量 与向量 垂直;
一、向量的夹角:
对于两个非零向量 和 ,若 , ,那么射
线OA、OB的夹角 叫做向量 与向量 的夹角。
二、向量的数量积:
记作
一般地,两个非零向量 、 的夹角为 ,
那么我们把 叫做向量 与向量 的数量积,
即
规定:
课堂小结
数量积的运算性质:
叫做向量 在向量 的方向上的投影。
课堂小结
数量积 的几何意义
作业
1. 练习册 8.2 A组 / 1,2 ; B组 / 1
2. 导学 P 78 -79 / 1 ~ 9
若 ,
若 ,
一、向量的夹角:
O
A
B
对于两个非零向量 和 , 作 , ,那么射线
OA、OB的夹角 叫做向量 与向量 的夹角。
若 ,
O
A
B
b
a
a 与b 同向
O
A
B
b
a
a 与b 反向
记作
O
A
B
a
b
a 与b 垂直,
平行
垂直
平行
一个物体在力 的作用下,从A移动到B处,位移为 ,
那么力 做的功是
一个物体在力 的作用下,从A移动到B处,位移为 ,
那么力 做的功是
记
称 为向量 与向量 的数量积。
二、向量的数量积:
记作
一般地,两个非零向量 、 的夹角为 ,
那么我们把 叫做向量 与向量 的数量积,
即
规定:
1、两个向量的数量积是一个
2、运算符“?”
特别地,
注意:
实数
不可写为“×”,也不能省略
A
B
C
例1: 如图,已知 ABC 是边长为6的正三角形,
求 与
例2: 判断以下运算是否正确,并说明理由:
注意区分:
向量的数量积
实数与向量的乘积
实数的乘法
数量积的运算性质:
数量积的运算性质:
研究 ?
叫做向量 在向量 的方向上的投影。
数量积 的几何意义是:
两个向量 、 的数量积是其中的一个向量 的模与
另一个向量 在向量 的方向上的投影 的乘积。
| b | cosθ>0
| b | cosθ<0
| b | cosθ=0
θ为锐角时,
θ为钝角时,
O
A
B
θ为直角时,
研究
O
C
B
A
C1
B1
例3: 用 表示
例4: 已知 且 与 的夹角为
求
(1)当 时,表示向量 与向量 方向相同;
(2)当 时,表示向量 与向量 方向相反;
(3)当 时,表示向量 与向量 垂直;
一、向量的夹角:
对于两个非零向量 和 ,若 , ,那么射
线OA、OB的夹角 叫做向量 与向量 的夹角。
二、向量的数量积:
记作
一般地,两个非零向量 、 的夹角为 ,
那么我们把 叫做向量 与向量 的数量积,
即
规定:
课堂小结
数量积的运算性质:
叫做向量 在向量 的方向上的投影。
课堂小结
数量积 的几何意义
作业
1. 练习册 8.2 A组 / 1,2 ; B组 / 1
2. 导学 P 78 -79 / 1 ~ 9
