沪教版(上海)数学高二上册-8.3 平面向量的分解定理 课件 (1)(16张PPT)
文档属性
| 名称 | 沪教版(上海)数学高二上册-8.3 平面向量的分解定理 课件 (1)(16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 21:27:04 | ||
图片预览





文档简介
平面向量的分解定理
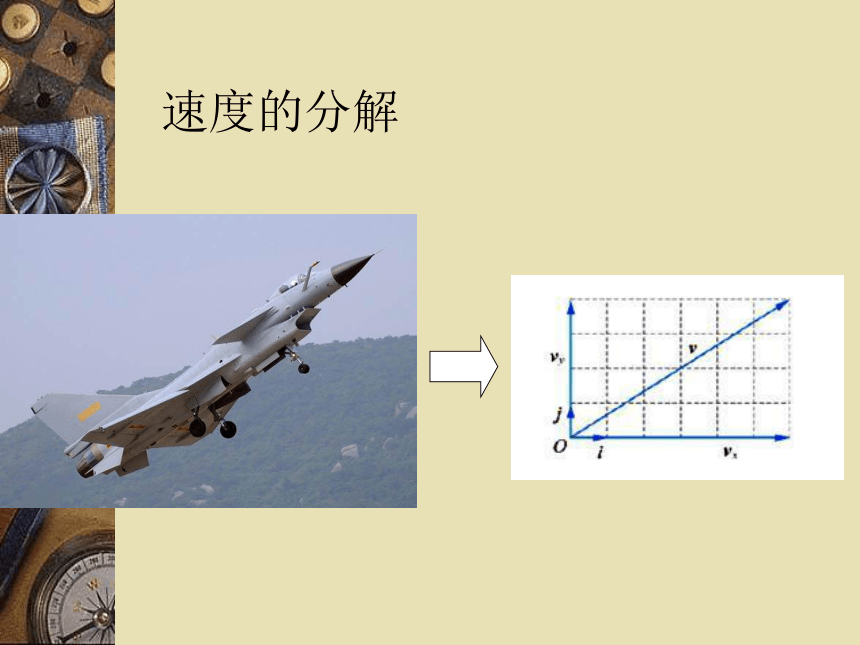
速度的分解
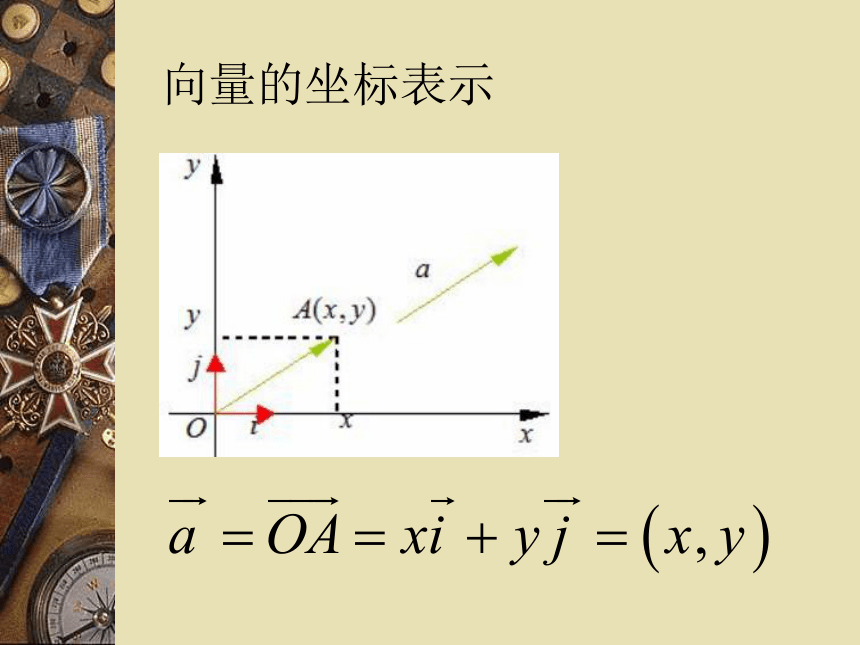
向量的坐标表示
平面向量的分解定理
平面向量的分解定理
1 任意向量都可以沿两个不平行的方向表示为两个向量的线性组合,并且这种分解是唯一的;
2 正交分解是平面向量分解定理的特例;
3 平面上的任意两个不平行的向量都可作为基;
4 只要给定平面内两个不平行向量 、 ,就可以用
来表示这一平面内所有的向量.
平面向量分解定理的应用
例1 如图,平行四边形的两条对角线相交于点 ,
且 , ,用 分别表示 、 、
、 .
A
B
C
D
M
平面向量分解定理的应用
例2 已知 为两不平行非零向量, ,
, ,试用 表示 .
平面向量分解定理的应用
例3 如图,在 中, , ,
, 是 边上一点, ,求
A
D
C
B
平面内三点共线的判定及性质
判定:平面上三点 满足
,且 ,则 三点共线.
性质:平面上三点 满足
, 三点共线,则 .
C
B
A
O
如何测算出风速呢?
平面向量分解定理的应用
例4 有一个小组得到以下数据,自行车以每秒3.8米的速度向东行驶,测得风自北方来,若以每秒5.6米的速度向东行驶,测得风自东北方来,求风速.
课堂小结
1.平面向量分解定理告诉我们,任意向量都可以沿两个不平行的方向表示为两个向量的线性组合,并且这种分解是唯一的;
2.其实质意义更在于:只要给定平面内两个不平行向量 ,就可以用来表示这一平面内所有的向量.
谢谢
速度的分解
向量的坐标表示
平面向量的分解定理
平面向量的分解定理
1 任意向量都可以沿两个不平行的方向表示为两个向量的线性组合,并且这种分解是唯一的;
2 正交分解是平面向量分解定理的特例;
3 平面上的任意两个不平行的向量都可作为基;
4 只要给定平面内两个不平行向量 、 ,就可以用
来表示这一平面内所有的向量.
平面向量分解定理的应用
例1 如图,平行四边形的两条对角线相交于点 ,
且 , ,用 分别表示 、 、
、 .
A
B
C
D
M
平面向量分解定理的应用
例2 已知 为两不平行非零向量, ,
, ,试用 表示 .
平面向量分解定理的应用
例3 如图,在 中, , ,
, 是 边上一点, ,求
A
D
C
B
平面内三点共线的判定及性质
判定:平面上三点 满足
,且 ,则 三点共线.
性质:平面上三点 满足
, 三点共线,则 .
C
B
A
O
如何测算出风速呢?
平面向量分解定理的应用
例4 有一个小组得到以下数据,自行车以每秒3.8米的速度向东行驶,测得风自北方来,若以每秒5.6米的速度向东行驶,测得风自东北方来,求风速.
课堂小结
1.平面向量分解定理告诉我们,任意向量都可以沿两个不平行的方向表示为两个向量的线性组合,并且这种分解是唯一的;
2.其实质意义更在于:只要给定平面内两个不平行向量 ,就可以用来表示这一平面内所有的向量.
谢谢
