沪教版(上海)数学高二上册-8.3 平面向量的分解定理 课件 (3)(38张PPT)
文档属性
| 名称 | 沪教版(上海)数学高二上册-8.3 平面向量的分解定理 课件 (3)(38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 21:31:34 | ||
图片预览








文档简介
8.3平面向量分解定理
一、学习目标
1.根据已有的物理知识经验,在熟悉的问题情景中,体会向量分解;
2.理解和掌握平面向量的分解定理;
3.掌握平面内任一向量都可以用两个不平行向量来表示;掌握基的概念,并能够用基表示平面内的向量。
二、学习重点及难点
平面向量分解定理的的探究;
分解唯一性的证明。
复习
:
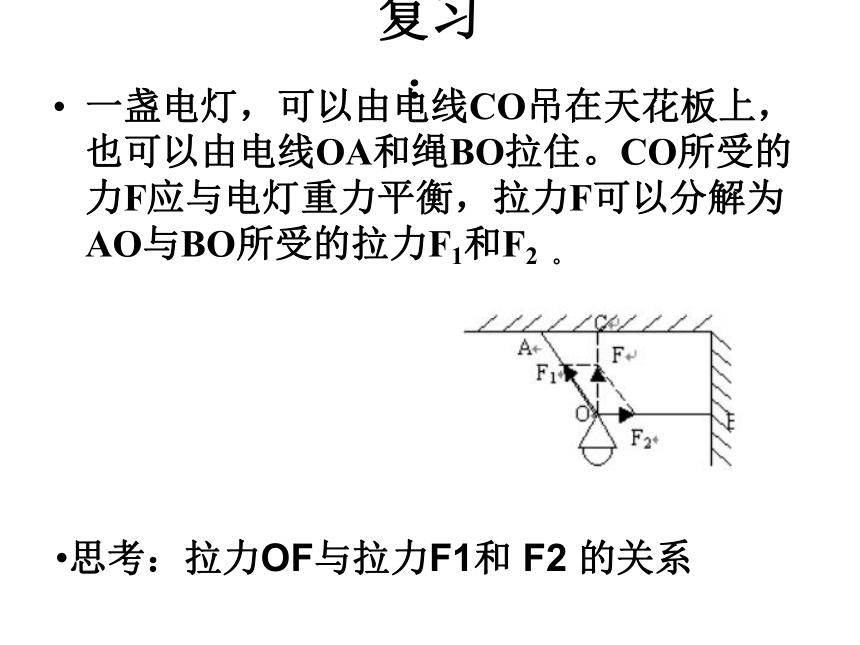
一盏电灯,可以由电线CO吊在天花板上,也可以由电线OA和绳BO拉住。CO所受的力F应与电灯重力平衡,拉力F可以分解为AO与BO所受的拉力F1和F2 。
思考:拉力OF与拉力F1和 F2 的关系
问题:前面我们学过向量的加法,知道两个向量可以合成一个向量,反过来,一个向量是否可以分解成两个向量呢?
复习
根据下面正交分解示意图,并完成填空
复习
从上例正交分解可以看出在平面直角坐标系中,任意向量可以分解成坐标轴正方向上单位向量的线性组合,且分解唯一。
思考:如果 是平面内的两个不平行的向量, 是该平面内的给定一个非零向量,那么 与 之间有什么关系呢?
活动步骤:
a.以小组为单位,每一位同学一个图,上面有两个不平行向量 和 ;
b.每个同学先独立作图;
c.小组对照,比较所分解的两向量的长度和方向是否相同?并得出结论。
学习活动1
给定平面内的两个不平行向量 ,对于给定的非零向量 是否能分解成 方向上的两个向量,且分解是否是唯一的?
活动目的:
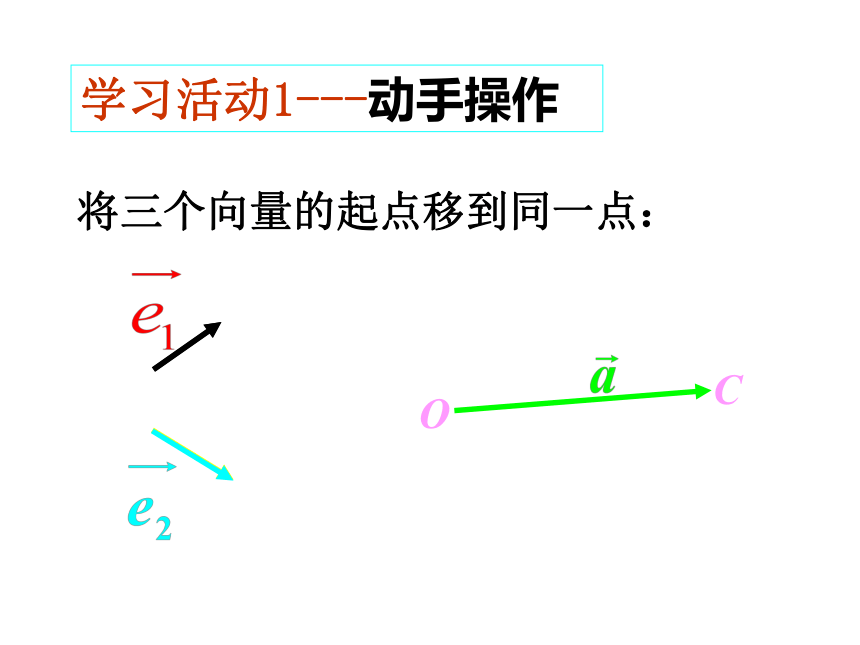
学习活动1---动手操作
将三个向量的起点移到同一点:
O
C
O
A
C
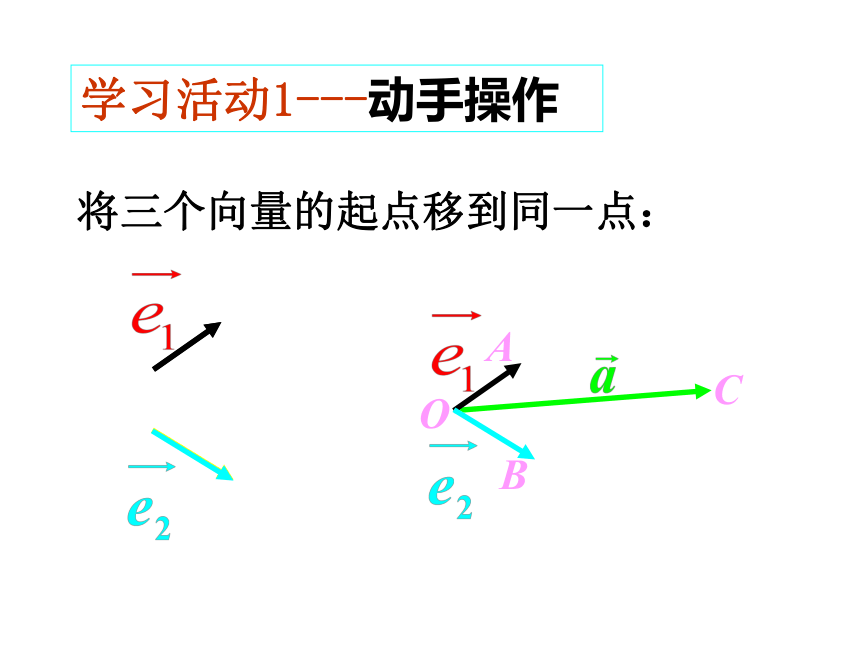
将三个向量的起点移到同一点:
学习活动1---动手操作
B
O
A
C
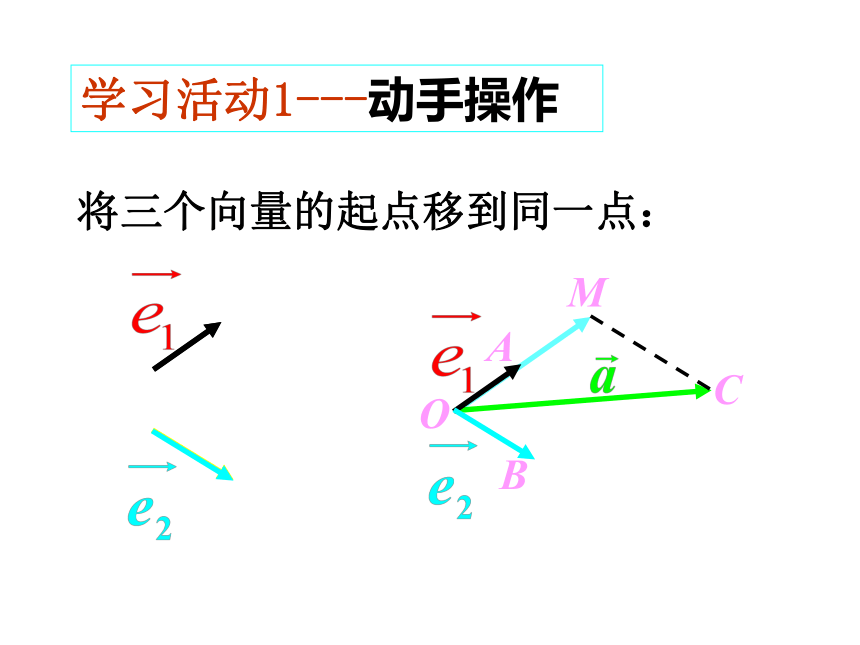
将三个向量的起点移到同一点:
学习活动1---动手操作
B
O
A
M
C
将三个向量的起点移到同一点:
学习活动1---动手操作
B
N
O
A
M
C
将三个向量的起点移到同一点:
学习活动1---动手操作
N
O
A
M
B
C
学习活动1---动手操作
N
O
A
M
B
C
学习活动1---活动结果
结论:可以分解,且分解的长度和方向唯一的。
思考:对于给定的向量可以唯一分解成给定的两个不平行向量,那么对于任意的向量 是否也可以得到同样的结论呢?
活动步骤:
a.以小组为单位,各小组的任务不一样,上面有两个不平行向量 和 ;
b.每个小组共同思考并完成作图;
c.各小组展示其成果并得出结论。
学习活动2
思考:对于给定的向量可以唯一分解成给定的两个不平行向量,那么对于任意的向量 是否也可以得到同样的结论呢?
活动目的:
通过小组之间的动手操作,让学生体会对于任意向量都可以分解成给定的两个不平行向量,且分解是唯一的.?
学习活动2---动手操作
B
O
O
A
B
C
A
C
学习活动2---动手操作
B
O
O
A
B
C
A
C
B'
学习活动2---动手操作
B'
O
A
M
B
C
B
O
A
C
学习活动2---动手操作
B'
O
A
M
B
N
C
B
O
A
C
学习活动2---动手操作
B
M
B'
O
O
A
M
B
N
C
A
C
A'
学习活动2---动手操作
B
N
M
B'
O
O
A
M
B
N
C
A
C
A'
学习活动2---动手操作
O
A
B
C
学习活动2---动手操作
A'
O
A
B
C
学习活动2---动手操作
O
A
B
B'
C
A'
学习活动2---动手操作
M
A'
O
A
B
B'
C
学习活动2---动手操作
N
M
A'
O
A
B
B'
C
学习活动2---动手操作
可以分解,且分解的长度和方向唯一的。
思考:我们对以上两个实验加以概括,可以得出怎样的结论 ?
结论:平面内的任一非零向量 都可以表示为给定的两个不平行向量 的线性表示,即 ,且分解是唯一的。
学习活动2---活动结果
证明:(1)当 时,
(2)当 时,假设 ,则有
由于 不平行,故 ,即 。
平面向量定理唯一性证明
平面向量分解定理:
如果 是平面内的两个不平行向量,那么对于这一平面内的任意向量 ,有且只有一对实数 ,使 ,我们把不平行的向量
叫做这一平面内所有向量的一组基(向量)。
注意:
(1)基底不共线;
(2)将任一向量 在给出基底 的条件下进行分解;
(3)基底给定时,分解形式唯一, 是被 , , 唯一确定的数量。
例题分析
例1
例2.如图:平行四边形ABCD的两条对角线相交于点M,且 ,分别用 表示
A
B
C
D
思考题:
如图,已知 是不平行的两个向量, 是实数,且 ,用 表示 .
O
A
B
P
课堂小结
(1)平面向量的分解定理. 对分解定理的理解:基底 为两个不平行向量,向量 的任意性,实数对 的存在性和唯一性;
(2)从基的角度认识几何图形。
作业布置:完成学案后作业
谢谢指导
一、学习目标
1.根据已有的物理知识经验,在熟悉的问题情景中,体会向量分解;
2.理解和掌握平面向量的分解定理;
3.掌握平面内任一向量都可以用两个不平行向量来表示;掌握基的概念,并能够用基表示平面内的向量。
二、学习重点及难点
平面向量分解定理的的探究;
分解唯一性的证明。
复习
:
一盏电灯,可以由电线CO吊在天花板上,也可以由电线OA和绳BO拉住。CO所受的力F应与电灯重力平衡,拉力F可以分解为AO与BO所受的拉力F1和F2 。
思考:拉力OF与拉力F1和 F2 的关系
问题:前面我们学过向量的加法,知道两个向量可以合成一个向量,反过来,一个向量是否可以分解成两个向量呢?
复习
根据下面正交分解示意图,并完成填空
复习
从上例正交分解可以看出在平面直角坐标系中,任意向量可以分解成坐标轴正方向上单位向量的线性组合,且分解唯一。
思考:如果 是平面内的两个不平行的向量, 是该平面内的给定一个非零向量,那么 与 之间有什么关系呢?
活动步骤:
a.以小组为单位,每一位同学一个图,上面有两个不平行向量 和 ;
b.每个同学先独立作图;
c.小组对照,比较所分解的两向量的长度和方向是否相同?并得出结论。
学习活动1
给定平面内的两个不平行向量 ,对于给定的非零向量 是否能分解成 方向上的两个向量,且分解是否是唯一的?
活动目的:
学习活动1---动手操作
将三个向量的起点移到同一点:
O
C
O
A
C
将三个向量的起点移到同一点:
学习活动1---动手操作
B
O
A
C
将三个向量的起点移到同一点:
学习活动1---动手操作
B
O
A
M
C
将三个向量的起点移到同一点:
学习活动1---动手操作
B
N
O
A
M
C
将三个向量的起点移到同一点:
学习活动1---动手操作
N
O
A
M
B
C
学习活动1---动手操作
N
O
A
M
B
C
学习活动1---活动结果
结论:可以分解,且分解的长度和方向唯一的。
思考:对于给定的向量可以唯一分解成给定的两个不平行向量,那么对于任意的向量 是否也可以得到同样的结论呢?
活动步骤:
a.以小组为单位,各小组的任务不一样,上面有两个不平行向量 和 ;
b.每个小组共同思考并完成作图;
c.各小组展示其成果并得出结论。
学习活动2
思考:对于给定的向量可以唯一分解成给定的两个不平行向量,那么对于任意的向量 是否也可以得到同样的结论呢?
活动目的:
通过小组之间的动手操作,让学生体会对于任意向量都可以分解成给定的两个不平行向量,且分解是唯一的.?
学习活动2---动手操作
B
O
O
A
B
C
A
C
学习活动2---动手操作
B
O
O
A
B
C
A
C
B'
学习活动2---动手操作
B'
O
A
M
B
C
B
O
A
C
学习活动2---动手操作
B'
O
A
M
B
N
C
B
O
A
C
学习活动2---动手操作
B
M
B'
O
O
A
M
B
N
C
A
C
A'
学习活动2---动手操作
B
N
M
B'
O
O
A
M
B
N
C
A
C
A'
学习活动2---动手操作
O
A
B
C
学习活动2---动手操作
A'
O
A
B
C
学习活动2---动手操作
O
A
B
B'
C
A'
学习活动2---动手操作
M
A'
O
A
B
B'
C
学习活动2---动手操作
N
M
A'
O
A
B
B'
C
学习活动2---动手操作
可以分解,且分解的长度和方向唯一的。
思考:我们对以上两个实验加以概括,可以得出怎样的结论 ?
结论:平面内的任一非零向量 都可以表示为给定的两个不平行向量 的线性表示,即 ,且分解是唯一的。
学习活动2---活动结果
证明:(1)当 时,
(2)当 时,假设 ,则有
由于 不平行,故 ,即 。
平面向量定理唯一性证明
平面向量分解定理:
如果 是平面内的两个不平行向量,那么对于这一平面内的任意向量 ,有且只有一对实数 ,使 ,我们把不平行的向量
叫做这一平面内所有向量的一组基(向量)。
注意:
(1)基底不共线;
(2)将任一向量 在给出基底 的条件下进行分解;
(3)基底给定时,分解形式唯一, 是被 , , 唯一确定的数量。
例题分析
例1
例2.如图:平行四边形ABCD的两条对角线相交于点M,且 ,分别用 表示
A
B
C
D
思考题:
如图,已知 是不平行的两个向量, 是实数,且 ,用 表示 .
O
A
B
P
课堂小结
(1)平面向量的分解定理. 对分解定理的理解:基底 为两个不平行向量,向量 的任意性,实数对 的存在性和唯一性;
(2)从基的角度认识几何图形。
作业布置:完成学案后作业
谢谢指导
