沪教版(上海)数学高二上册-8.4 空间向量在度量问题中的应用 课件(13张PPT)
文档属性
| 名称 | 沪教版(上海)数学高二上册-8.4 空间向量在度量问题中的应用 课件(13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 21:33:34 | ||
图片预览




文档简介
空间向量在度量问题中的应用
空间向量的相关知识
1、平行垂直问题
(一)复习巩固
2、夹角问题
(结合图象,直观感觉)
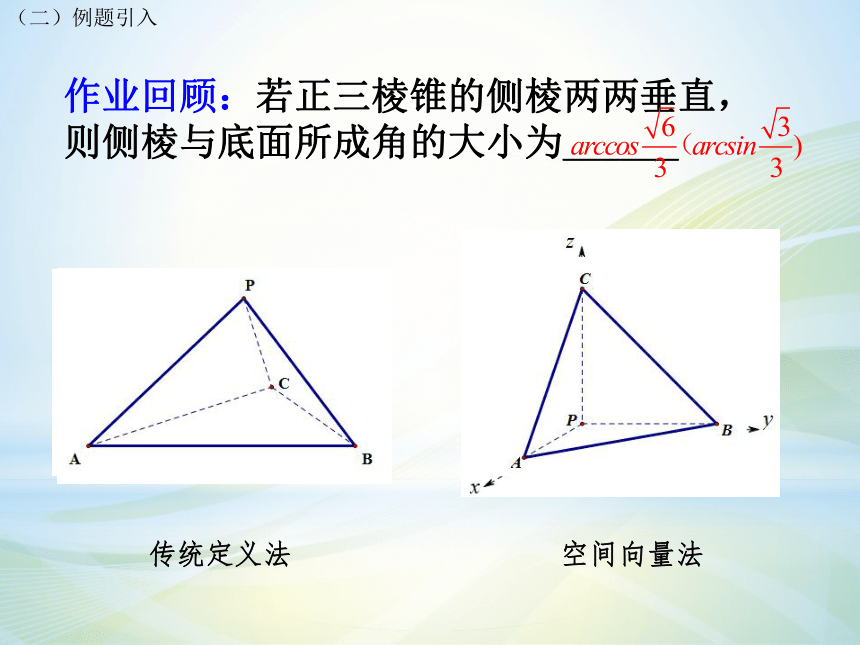
作业回顾:若正三棱锥的侧棱两两垂直,则侧棱与底面所成角的大小为______
传统定义法
空间向量法
(二)例题引入
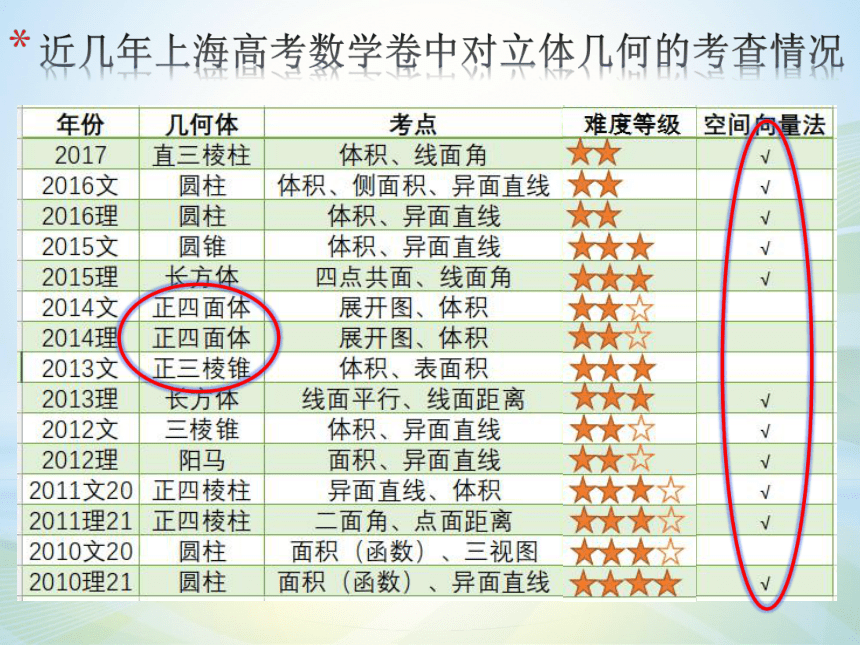
近几年上海高考数学卷中对立体几何的考查情况
例1、
如图,已知正三棱柱
ABC
-
A
1
B
1
C
1
的
底面边长为
2
,侧棱长为
3
2
,点
E
在侧棱
AA
1
上,点
F
在侧棱
BB
1
上,且
AE
=
2
2
,
BF
=
2
.
求证:
CF
⊥
C
1
E.
方法一
证明
由已知可得
CC
1
=
3
2
,
CE
=
C
1
F
=
2
2
+
(
2
2
)
2
=
2
3
,
EF
2
=
AB
2
+
(
AE
-
BF
)
2
,
EF
=
C
1
E
=
2
2
+
(
2
)
2
=
6
,
于是有
EF
2
+
C
1
E
2
=
C
1
F
2
,
CE
2
+
C
1
E
2
=
CC
2
1
,
所以
C
1
E
⊥
EF
,
C
1
E
⊥
CE
.
又
EF
∩
CE
=
E
,所以
C
1
E
⊥
平面
CEF
.
又
CF
?
平面
CEF
,故
CF
⊥
C
1
E
.
(三)范例分析
方法二
建立如图所示的空间直角坐标系,
则由已知可得
C
(0,2,0)
,
C
1
(0,2,3
2
)
,
E
(0,0,2
2
)
,
F
(
3
,
1
,
2
)
.
证明
C
1
E
→
=
(0
,-
2
,-
2
)
,
CF
→
=
(
3
,-
1
,
2
)
,
C
1
E
→
·
CF
→
=
0
+
2
-
2
=
0.
所以
CF
⊥
C
1
E
.
已知正方体
ABCD
-
A
1
B
1
C
1
D
1
的棱长为
1
,点
P
在线段
BD
1
上,当
∠
APC
最大时,三棱锥
P
-
ABC
的体积为
____
__
.
例2、
(1)
证明
连结
BD
,设
AC
交
BD
于
O
,则
AC
⊥
BD
.
由题意知
SO
⊥
平面
ABCD
.
以
O
为坐标原点,
OB
→
,
OC
→
,
OS
→
分别为
x
轴、
y
轴、
z
轴正方向,建立空间直角坐
标系如图.
如图所示,四棱锥
S
—
ABCD
的底面
是正方形,每条侧棱的长都是底面边长的
2
倍,
P
为侧棱
SD
上的点.
(1)
求证:
AC
⊥
SD
.
(2)
若
SD
⊥
平面
PAC
,则侧棱
SC
上是否存在一点
E
,使得
BE
∥
平面
PAC
.
若存在,求
SE
∶
EC
的值;若不存在,试说
明理由.
例3、
(四)课堂小结
1、 大部分立体几何题都可以采用向量法解决,向量法有效地降低了思维难度。
2、 空间向量法的步骤:
建系→求点(设点)→求向量→应用公式→作答。
3、 空间向量法侧重计算和传统定义法侧重理论,两者都需要一定的空间想象能力。
(五)巩固练习
空间向量的相关知识
1、平行垂直问题
(一)复习巩固
2、夹角问题
(结合图象,直观感觉)
作业回顾:若正三棱锥的侧棱两两垂直,则侧棱与底面所成角的大小为______
传统定义法
空间向量法
(二)例题引入
近几年上海高考数学卷中对立体几何的考查情况
例1、
如图,已知正三棱柱
ABC
-
A
1
B
1
C
1
的
底面边长为
2
,侧棱长为
3
2
,点
E
在侧棱
AA
1
上,点
F
在侧棱
BB
1
上,且
AE
=
2
2
,
BF
=
2
.
求证:
CF
⊥
C
1
E.
方法一
证明
由已知可得
CC
1
=
3
2
,
CE
=
C
1
F
=
2
2
+
(
2
2
)
2
=
2
3
,
EF
2
=
AB
2
+
(
AE
-
BF
)
2
,
EF
=
C
1
E
=
2
2
+
(
2
)
2
=
6
,
于是有
EF
2
+
C
1
E
2
=
C
1
F
2
,
CE
2
+
C
1
E
2
=
CC
2
1
,
所以
C
1
E
⊥
EF
,
C
1
E
⊥
CE
.
又
EF
∩
CE
=
E
,所以
C
1
E
⊥
平面
CEF
.
又
CF
?
平面
CEF
,故
CF
⊥
C
1
E
.
(三)范例分析
方法二
建立如图所示的空间直角坐标系,
则由已知可得
C
(0,2,0)
,
C
1
(0,2,3
2
)
,
E
(0,0,2
2
)
,
F
(
3
,
1
,
2
)
.
证明
C
1
E
→
=
(0
,-
2
,-
2
)
,
CF
→
=
(
3
,-
1
,
2
)
,
C
1
E
→
·
CF
→
=
0
+
2
-
2
=
0.
所以
CF
⊥
C
1
E
.
已知正方体
ABCD
-
A
1
B
1
C
1
D
1
的棱长为
1
,点
P
在线段
BD
1
上,当
∠
APC
最大时,三棱锥
P
-
ABC
的体积为
____
__
.
例2、
(1)
证明
连结
BD
,设
AC
交
BD
于
O
,则
AC
⊥
BD
.
由题意知
SO
⊥
平面
ABCD
.
以
O
为坐标原点,
OB
→
,
OC
→
,
OS
→
分别为
x
轴、
y
轴、
z
轴正方向,建立空间直角坐
标系如图.
如图所示,四棱锥
S
—
ABCD
的底面
是正方形,每条侧棱的长都是底面边长的
2
倍,
P
为侧棱
SD
上的点.
(1)
求证:
AC
⊥
SD
.
(2)
若
SD
⊥
平面
PAC
,则侧棱
SC
上是否存在一点
E
,使得
BE
∥
平面
PAC
.
若存在,求
SE
∶
EC
的值;若不存在,试说
明理由.
例3、
(四)课堂小结
1、 大部分立体几何题都可以采用向量法解决,向量法有效地降低了思维难度。
2、 空间向量法的步骤:
建系→求点(设点)→求向量→应用公式→作答。
3、 空间向量法侧重计算和传统定义法侧重理论,两者都需要一定的空间想象能力。
(五)巩固练习
