沪教版(上海)数学高二上册-8.4 平面向量在三角证明中的应用 课件(13张PPT)
文档属性
| 名称 | 沪教版(上海)数学高二上册-8.4 平面向量在三角证明中的应用 课件(13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 00:00:00 | ||
图片预览




文档简介
平面向量在三角证明中的应用
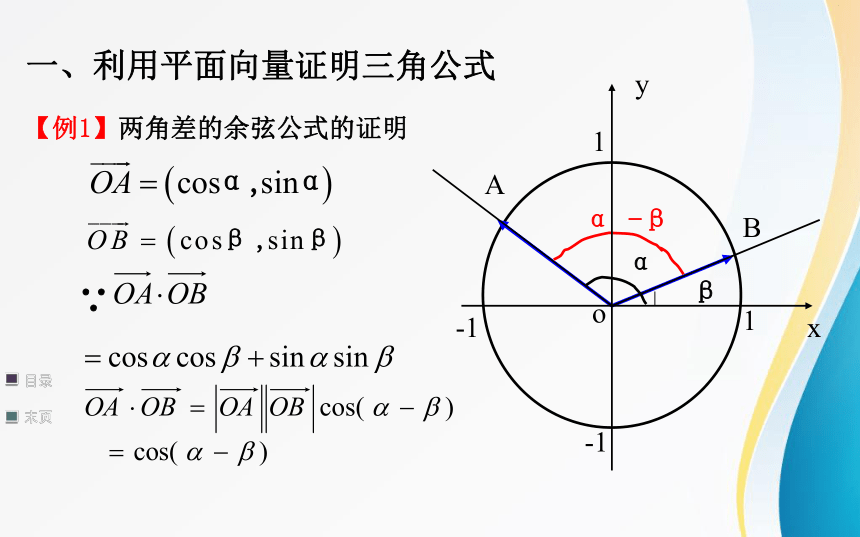
一、利用平面向量证明三角公式
【例1】两角差的余弦公式的证明
-1
1
1
-1
α -β
B
A
y
x
o
β
α
∵
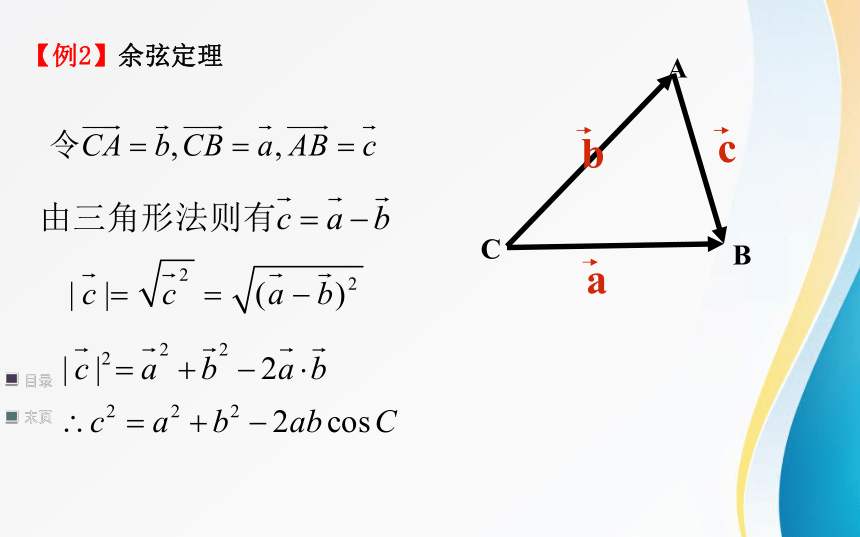
【例2】余弦定理
B
A
C
a
b
c
O是
的重心
P是△ABC所在平面内任一点.G是△ABC的重心
证明:
∵G是△ABC的重心
即
由此可得
(反之亦然(证略))
【例3】
【例3】
三、平面向量在三角形计算中的应用
【例3】
【课后作业】
5.设向量 =(4cos α,sin α), =(sin β,4cos β),
=(cos β,-4sin β).
(1)若 与 -2 垂直,求tan(α+β)的值.
(2)求| + |的最大值.
(3)若tan αtan β=16,求证: ∥ .
【解析】(1)因为b-2c=(sin β-2cos β,4cos β+8sin β),
a与b-2c垂直,
所以4cos α(sin β-2cos β)+sin α(4cos β+8sin β)=0,
即sin αcos β+cos αsin β
=2(cos αcos β-sin αsin β),
所以sin(α+β)=2cos(α+β),
所以tan(α+β)=2.
(2)因为b+c=(sin β+cos β,4cos β-4sin β),
所以|b+c|=
所以当sin 2β=-1时,|b+c|取最大值,且最大值为
(3)因为tan αtan β=16,
所以
即sin αsin β=16cos αcos β,
所以(4cos α)·(4cos β)=sin αsin β,
即a=(4cos α,sin α)与b=(sin β,4cos β)共线,
所以a∥b.
一、利用平面向量证明三角公式
【例1】两角差的余弦公式的证明
-1
1
1
-1
α -β
B
A
y
x
o
β
α
∵
【例2】余弦定理
B
A
C
a
b
c
O是
的重心
P是△ABC所在平面内任一点.G是△ABC的重心
证明:
∵G是△ABC的重心
即
由此可得
(反之亦然(证略))
【例3】
【例3】
三、平面向量在三角形计算中的应用
【例3】
【课后作业】
5.设向量 =(4cos α,sin α), =(sin β,4cos β),
=(cos β,-4sin β).
(1)若 与 -2 垂直,求tan(α+β)的值.
(2)求| + |的最大值.
(3)若tan αtan β=16,求证: ∥ .
【解析】(1)因为b-2c=(sin β-2cos β,4cos β+8sin β),
a与b-2c垂直,
所以4cos α(sin β-2cos β)+sin α(4cos β+8sin β)=0,
即sin αcos β+cos αsin β
=2(cos αcos β-sin αsin β),
所以sin(α+β)=2cos(α+β),
所以tan(α+β)=2.
(2)因为b+c=(sin β+cos β,4cos β-4sin β),
所以|b+c|=
所以当sin 2β=-1时,|b+c|取最大值,且最大值为
(3)因为tan αtan β=16,
所以
即sin αsin β=16cos αcos β,
所以(4cos α)·(4cos β)=sin αsin β,
即a=(4cos α,sin α)与b=(sin β,4cos β)共线,
所以a∥b.
