沪教版(上海)数学高三上册-15.1 多面体的截面 课件(共19张PPT)
文档属性
| 名称 | 沪教版(上海)数学高三上册-15.1 多面体的截面 课件(共19张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 395.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 09:57:04 | ||
图片预览


文档简介
多面体的截面
多面体截面的概念和性质
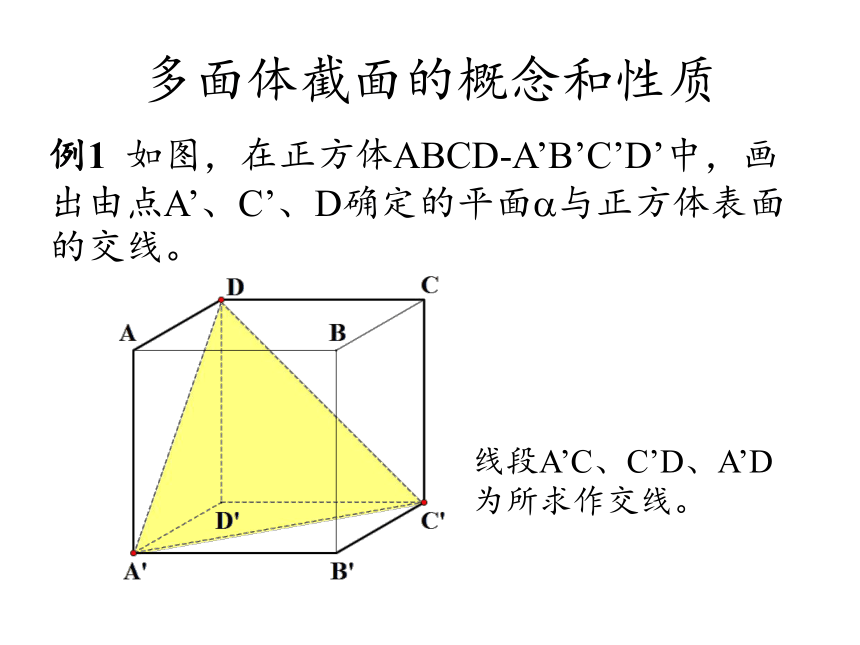
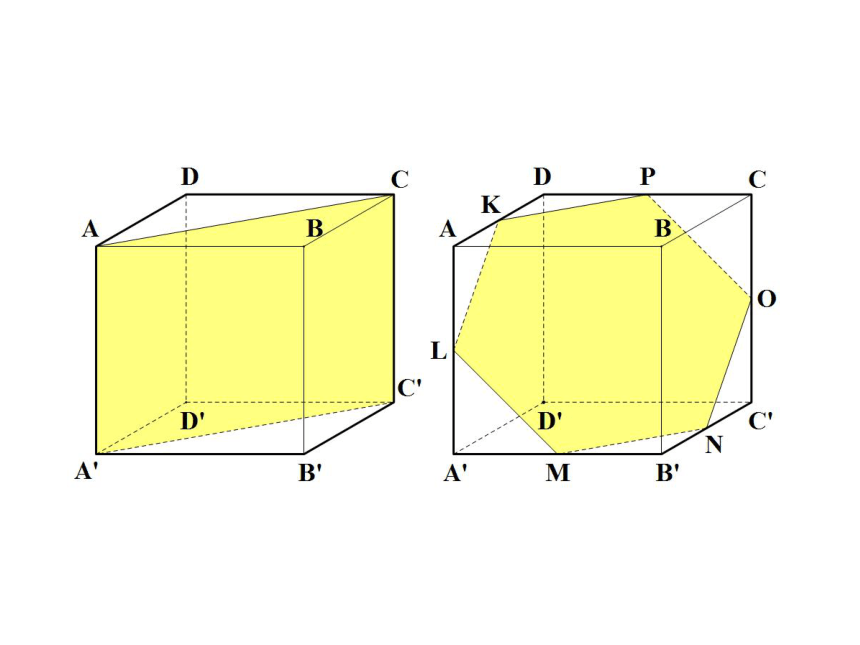
例1 如图,在正方体ABCD-A’B’C’D’中,画出由点A’、C’、D确定的平面?与正方体表面的交线。
线段A’C、C’D、A’D为所求作交线。
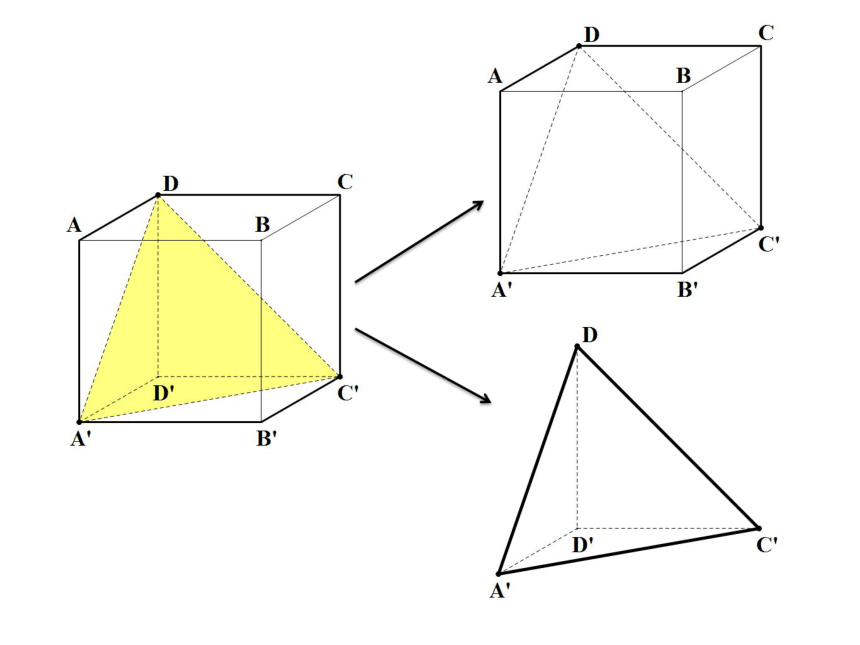
思考
平面截多面体的截面是否一定是三角形?如果不一定,那它是什么图形?
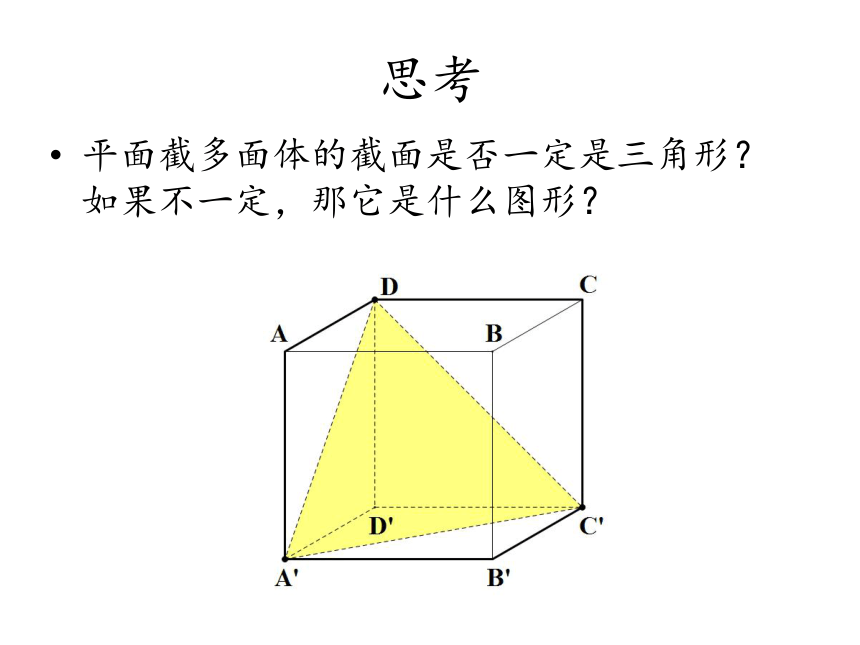
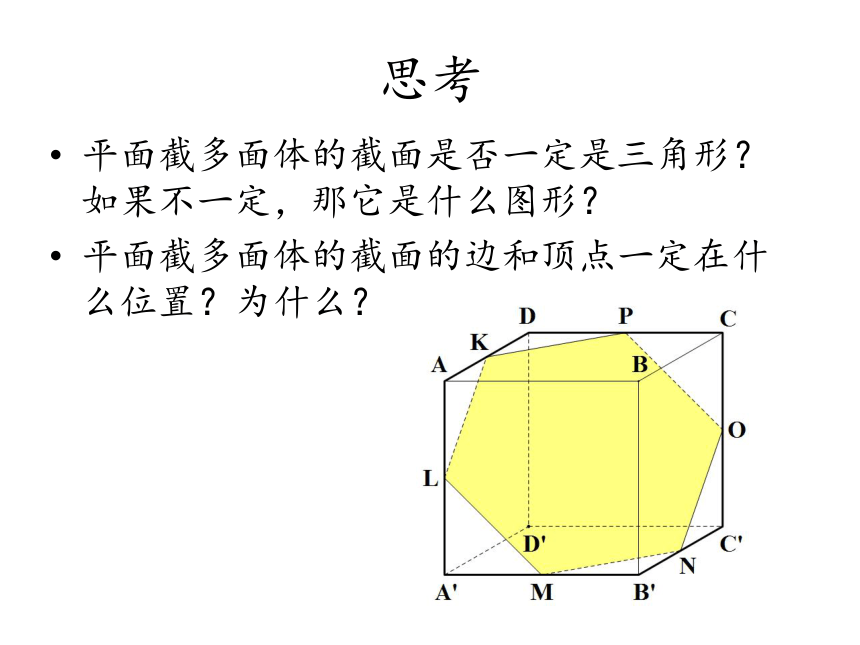
思考
平面截多面体的截面是否一定是三角形?如果不一定,那它是什么图形?
平面截多面体的截面的边和顶点一定在什么位置?为什么?
多面体截面的画法
例2 如图,在长方体ABCD-A’B’C’D’中,点E是面CDD’C’内一点,画出由点A’、C’、E确定的平面?截正方体的截面。
截面A’C’F为所求作截面。
连:作平面?与多面体一个面的两个公共点的连线段
延:延长连线段,在面上形成交线
找:找其他面上与已知交线所在直线共面相交的直线
交:作两直线的交点,即平面?与其他面的公共点
检:检验所画图形是否满足截面概念及性质
例2变式 如图,在长方体ABCD-A’B’C’D’中,点E是棱CD上一点,画出由点A’、C’、E确定的平面?截正方体的截面。
截面A’C’EG为所求作截面。
例2变式 如图,在长方体ABCD-A’B’C’D’中,点E是棱CD上一点,画出由点A’、C’、E确定的平面?截正方体的截面。
截面A’C’EG为所求作截面。
例3 如图,在正方体ABCD-A’B’C’D’中,点E、点F分别在棱CD、棱B’C’上,画出由点A’、E、F确定的平面?截正方体的截面。
巩固练习 如图,在正方体ABCD-A’B’C’D’中,点E、F、G分别是棱A’B’、B’C’、CD的中点,画出由点E、F、G确定的平面?截正方体的截面。
课堂小结
多面体截面的概念
当一个平面截多面体时,多面体的表面与平面的______所围成的平面图形叫做平面截多面体的截面。因此画截面的目标是画多面体的表面与平面的______,作交线的关键是找多面体的面与平面的___________。
多面体截面的性质
多面体的截面是____________,截面的边在多面体的_____上;顶点在多面体的______上。
“交线法”的具体步骤
连→延→找→交→检
交线
平面多边形
面
棱
交线
两个公共点
拓展研究
练习1 如图,在三棱柱ABC-A’B’C’中,点P、Q、R分别在棱AA’、BB’、A’C’上,画出由点P、Q、R确定的平面?截三棱柱的截面。
练习2 如图,在四棱锥S-ABCD中,点P、Q、R分别在棱AD、BC、CS上,画出由点P、Q、R确定的平面?截四棱锥的截面。
回家作业
《多面体的截面》作业卷
思考:如果多面体不是长方体,作截面方法是否相同?
思考:如果确定平面的三点中,没有两点在多面体的同一面上,该如何作截面?
拓展研究
1、如图,在四棱锥S-ABCD中,点P、Q、R分别在棱AD、BC、CS上,画出由点P、Q、R确定的平面?截四棱锥的截面。
拓展研究
2、 如图,在长方体ABCD-A’B’C’D’中,点E、F、G分别在棱AD、A’B’、CC’上,画出由点E、F、G确定的平面?截正方体的截面。
多面体截面的概念和性质
例1 如图,在正方体ABCD-A’B’C’D’中,画出由点A’、C’、D确定的平面?与正方体表面的交线。
线段A’C、C’D、A’D为所求作交线。
思考
平面截多面体的截面是否一定是三角形?如果不一定,那它是什么图形?
思考
平面截多面体的截面是否一定是三角形?如果不一定,那它是什么图形?
平面截多面体的截面的边和顶点一定在什么位置?为什么?
多面体截面的画法
例2 如图,在长方体ABCD-A’B’C’D’中,点E是面CDD’C’内一点,画出由点A’、C’、E确定的平面?截正方体的截面。
截面A’C’F为所求作截面。
连:作平面?与多面体一个面的两个公共点的连线段
延:延长连线段,在面上形成交线
找:找其他面上与已知交线所在直线共面相交的直线
交:作两直线的交点,即平面?与其他面的公共点
检:检验所画图形是否满足截面概念及性质
例2变式 如图,在长方体ABCD-A’B’C’D’中,点E是棱CD上一点,画出由点A’、C’、E确定的平面?截正方体的截面。
截面A’C’EG为所求作截面。
例2变式 如图,在长方体ABCD-A’B’C’D’中,点E是棱CD上一点,画出由点A’、C’、E确定的平面?截正方体的截面。
截面A’C’EG为所求作截面。
例3 如图,在正方体ABCD-A’B’C’D’中,点E、点F分别在棱CD、棱B’C’上,画出由点A’、E、F确定的平面?截正方体的截面。
巩固练习 如图,在正方体ABCD-A’B’C’D’中,点E、F、G分别是棱A’B’、B’C’、CD的中点,画出由点E、F、G确定的平面?截正方体的截面。
课堂小结
多面体截面的概念
当一个平面截多面体时,多面体的表面与平面的______所围成的平面图形叫做平面截多面体的截面。因此画截面的目标是画多面体的表面与平面的______,作交线的关键是找多面体的面与平面的___________。
多面体截面的性质
多面体的截面是____________,截面的边在多面体的_____上;顶点在多面体的______上。
“交线法”的具体步骤
连→延→找→交→检
交线
平面多边形
面
棱
交线
两个公共点
拓展研究
练习1 如图,在三棱柱ABC-A’B’C’中,点P、Q、R分别在棱AA’、BB’、A’C’上,画出由点P、Q、R确定的平面?截三棱柱的截面。
练习2 如图,在四棱锥S-ABCD中,点P、Q、R分别在棱AD、BC、CS上,画出由点P、Q、R确定的平面?截四棱锥的截面。
回家作业
《多面体的截面》作业卷
思考:如果多面体不是长方体,作截面方法是否相同?
思考:如果确定平面的三点中,没有两点在多面体的同一面上,该如何作截面?
拓展研究
1、如图,在四棱锥S-ABCD中,点P、Q、R分别在棱AD、BC、CS上,画出由点P、Q、R确定的平面?截四棱锥的截面。
拓展研究
2、 如图,在长方体ABCD-A’B’C’D’中,点E、F、G分别在棱AD、A’B’、CC’上,画出由点E、F、G确定的平面?截正方体的截面。
