沪教版(上海)数学高三上册-15.1 多面体的直观图 课件(共29张PPT)
文档属性
| 名称 | 沪教版(上海)数学高三上册-15.1 多面体的直观图 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 573.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 10:01:16 | ||
图片预览



文档简介
15.2 多面体的直观图
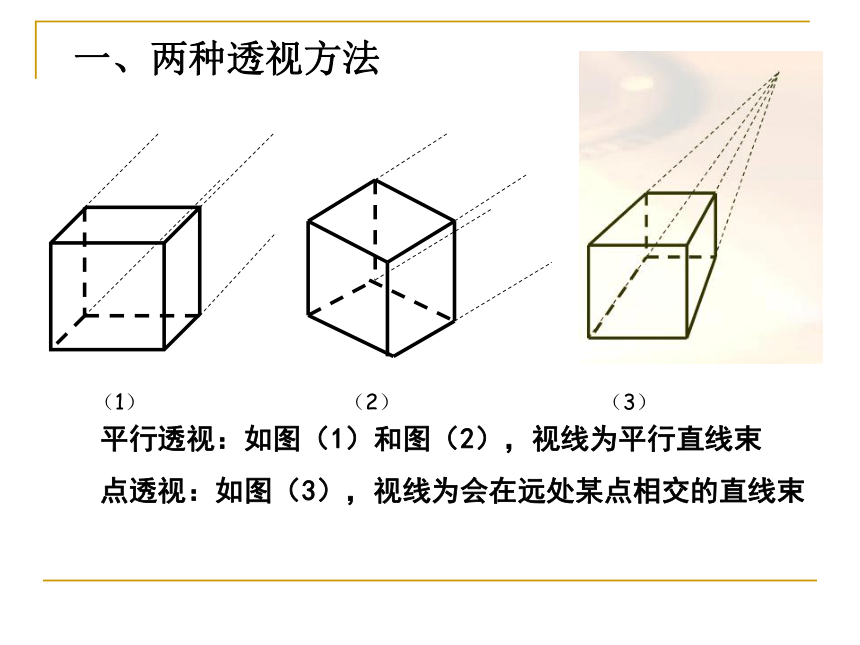
一、两种透视方法
(1)
(2)
(3)
平行透视:如图(1)和图(2),视线为平行直线束
点透视:如图(3),视线为会在远处某点相交的直线束
二、斜二轴测图画法(斜二测画法)
x
y
z
1350
(1)规定按图所示的位置和夹角
作三条轴分别表示铅垂方向、左右
方向以及前后方向,依次把它们叫做z轴,y轴,x轴
(2)规定z轴和y轴方向上的线段的长度
与其表示的真实长度相等,而在x轴方向上,
线段的长度是其表示的真实长度的二分之一.
用这种方法画的空间图形的直观图叫做斜二轴测图,这种画图方法简称“斜二测”画图法
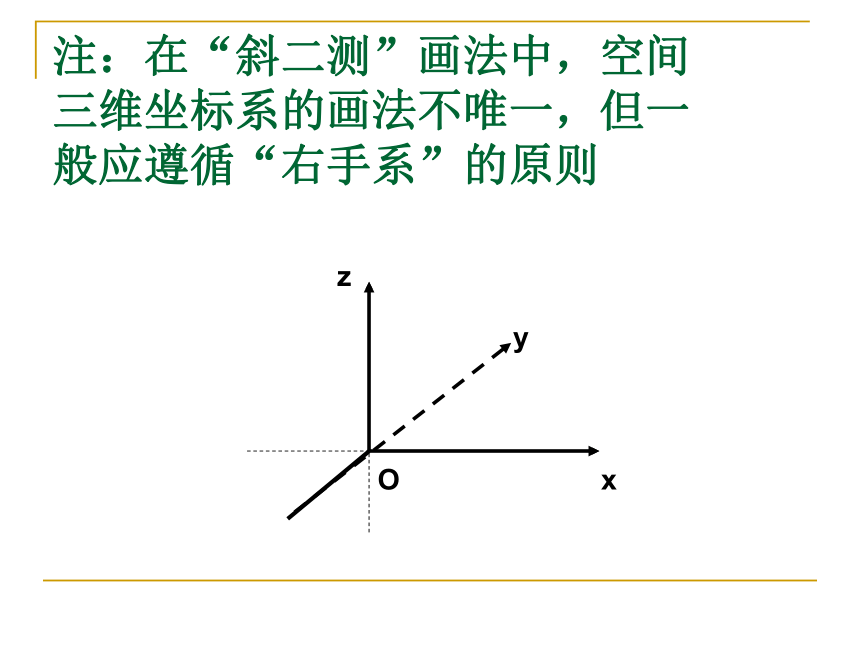
注:在“斜二测”画法中,空间三维坐标系的画法不唯一,但一般应遵循“右手系”的原则
x
O
y
z
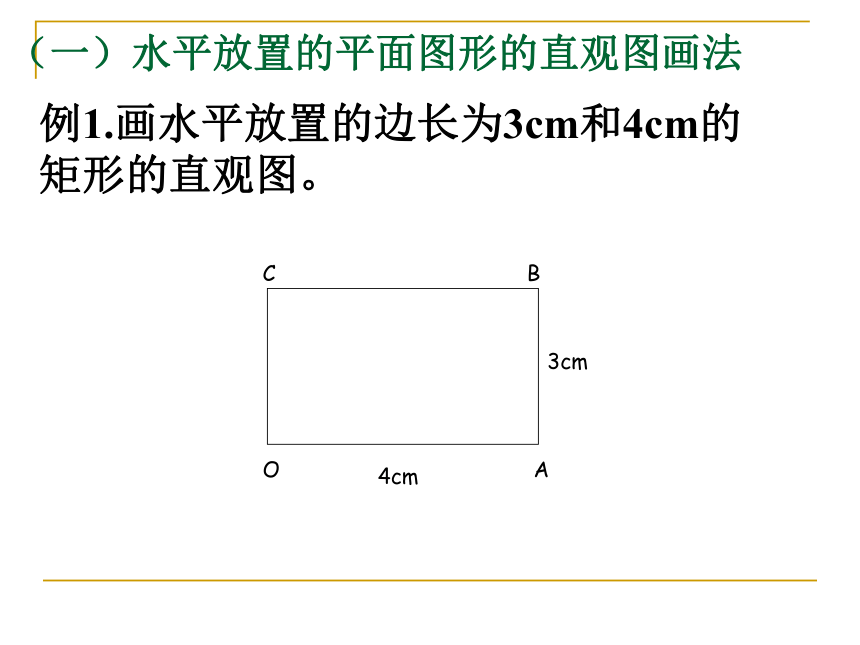
(一)水平放置的平面图形的直观图画法
例1.画水平放置的边长为3cm和4cm的矩形的直观图。
4cm
O
A
B
C
3cm
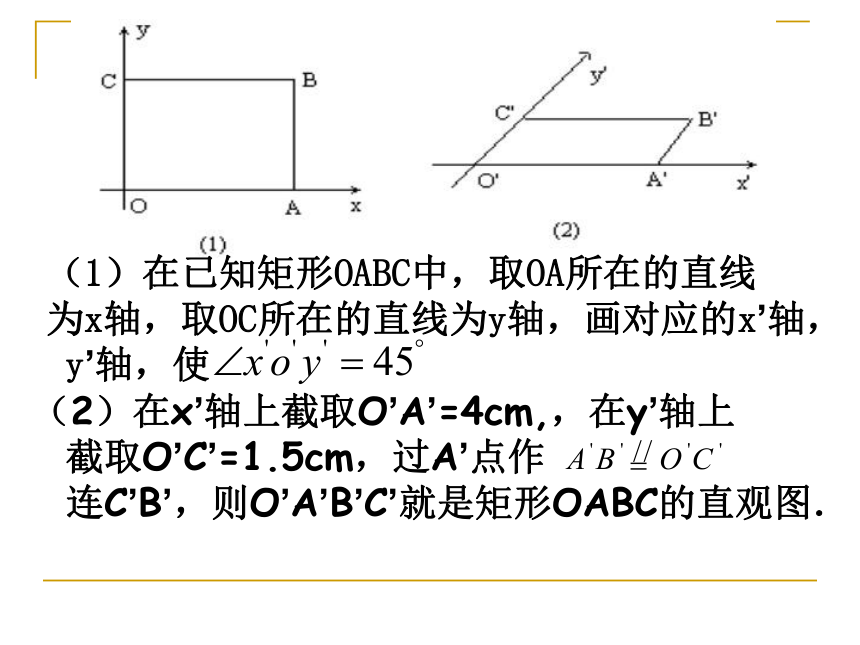
(1)在已知矩形OABC中,取OA所在的直线
为x轴,取OC所在的直线为y轴,画对应的x’轴,
y’轴,使
(2)在x’轴上截取O’A’=4cm,,在y’轴上
截取O’C’=1.5cm,过A’点作
连C’B’,则O’A’B’C’就是矩形OABC的直观图.
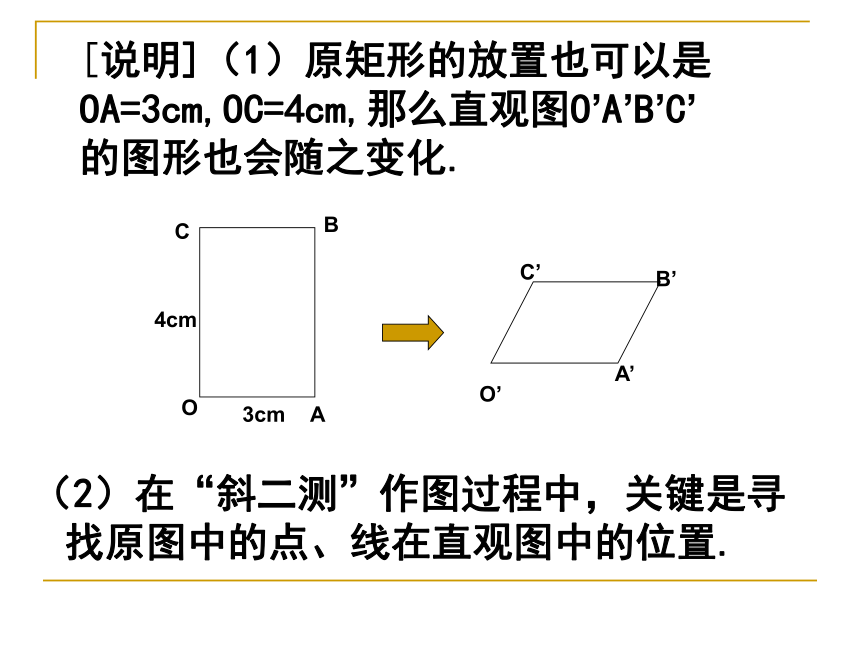
[说明](1)原矩形的放置也可以是 OA=3cm,OC=4cm,那么直观图O’A’B’C’
的图形也会随之变化.
(2)在“斜二测”作图过程中,关键是寻找原图中的点、线在直观图中的位置.
B
O
A
C
3cm
4cm
O’
A’
B’
C’
练习:画水平放置的直角梯形的直观图.
A
B
C
D
3
4
5
Y’
X’
A’
B’
C’
D’
2
3
5
A
B
C
D
3
4
5
x
y
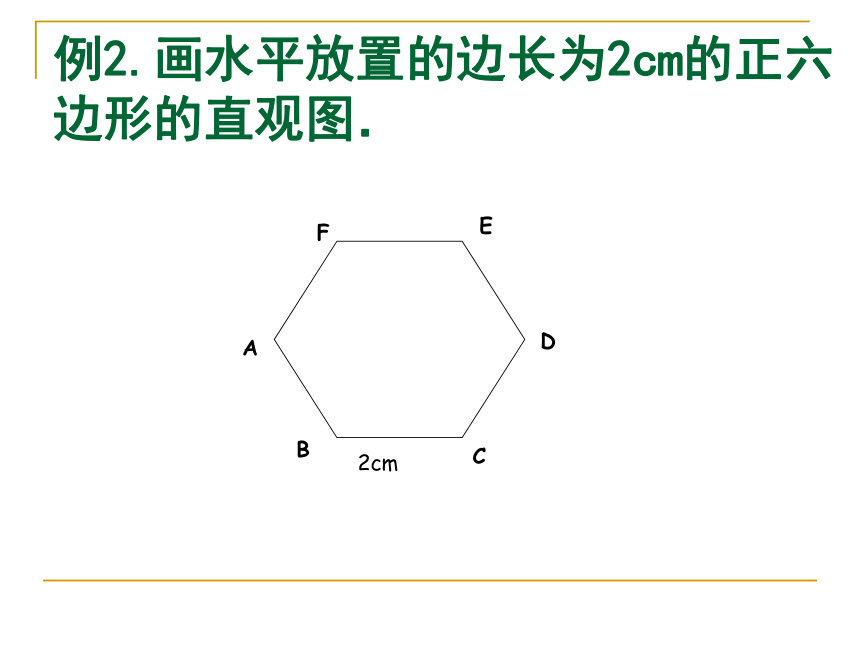
例2.画水平放置的边长为2cm的正六 边形的直观图.
2cm
A
B
C
D
E
F
[说明]] 在斜二测画法中,直观图
仍保留了原图中三个主要的性质:
第一,保平行.
第二,保共点、共线.
第三,保平行线段的比不变.
正因为有这“三保”,所以直观图的形状
虽然有很大的变化,但我们仍能借助于
直观图加上概念想象出原图的形状和性质.
A
B
C
D
E
F
O
O’
用“斜二测”画法画平面图形的要领:
横同,竖半,平行性不变
一句话小结:
1、已知矩形的面积是a,求用斜二测画法得到的直观图的面积。
问题拓展
2、如图,一个水平放置的平面图形的斜二测直观图是一个等腰梯形,它的底角为45度,两腰和上底边长均为1,求这个平面图形的面积,并说明它是什么图形。
A’
B’
C’
D’
X’
y’
1
1
A
B
C
D
1
2
问题拓展
(二)空间几何体的直观图的画法
x
y
z
1350
x
O
y
z
x
y
z
A
B
C
D
A’
B’
D’
C’
D
C
A’
D’
C’
A
B
B’
例3 .画棱长为2cm的正方体的直观图
总结:画空间图形(柱体、锥体)的直观图的步骤:
建系
画一个底面
画侧棱
成 图
课后探索1:画正三棱柱ABC-A’B’C’的直观图,使它的底面是边长为2cm的正三角形,
高度是3cm.
课后探索2:画三棱锥的直观图,使它的底面是腰长为a的等腰直角三角形,过直角顶点的侧棱长为a,且垂直于底面.
例1、已知:
画出过A、B、C三点的平面 的交线
A
C
B
(1)
D
画截面问题
A
C
B
(2)
A
C
B
(3)
D
D
E
F
例2:如图,P,Q,R分别是空间四边形ABCD的边AB,AD,BC上的点,且PQ与BD不平行,试画出平面PQR与平面BCD的交线.
E
F
A
B
A
F
E
E
F
E
F
G
H
一、两种透视方法
(1)
(2)
(3)
平行透视:如图(1)和图(2),视线为平行直线束
点透视:如图(3),视线为会在远处某点相交的直线束
二、斜二轴测图画法(斜二测画法)
x
y
z
1350
(1)规定按图所示的位置和夹角
作三条轴分别表示铅垂方向、左右
方向以及前后方向,依次把它们叫做z轴,y轴,x轴
(2)规定z轴和y轴方向上的线段的长度
与其表示的真实长度相等,而在x轴方向上,
线段的长度是其表示的真实长度的二分之一.
用这种方法画的空间图形的直观图叫做斜二轴测图,这种画图方法简称“斜二测”画图法
注:在“斜二测”画法中,空间三维坐标系的画法不唯一,但一般应遵循“右手系”的原则
x
O
y
z
(一)水平放置的平面图形的直观图画法
例1.画水平放置的边长为3cm和4cm的矩形的直观图。
4cm
O
A
B
C
3cm
(1)在已知矩形OABC中,取OA所在的直线
为x轴,取OC所在的直线为y轴,画对应的x’轴,
y’轴,使
(2)在x’轴上截取O’A’=4cm,,在y’轴上
截取O’C’=1.5cm,过A’点作
连C’B’,则O’A’B’C’就是矩形OABC的直观图.
[说明](1)原矩形的放置也可以是 OA=3cm,OC=4cm,那么直观图O’A’B’C’
的图形也会随之变化.
(2)在“斜二测”作图过程中,关键是寻找原图中的点、线在直观图中的位置.
B
O
A
C
3cm
4cm
O’
A’
B’
C’
练习:画水平放置的直角梯形的直观图.
A
B
C
D
3
4
5
Y’
X’
A’
B’
C’
D’
2
3
5
A
B
C
D
3
4
5
x
y
例2.画水平放置的边长为2cm的正六 边形的直观图.
2cm
A
B
C
D
E
F
[说明]] 在斜二测画法中,直观图
仍保留了原图中三个主要的性质:
第一,保平行.
第二,保共点、共线.
第三,保平行线段的比不变.
正因为有这“三保”,所以直观图的形状
虽然有很大的变化,但我们仍能借助于
直观图加上概念想象出原图的形状和性质.
A
B
C
D
E
F
O
O’
用“斜二测”画法画平面图形的要领:
横同,竖半,平行性不变
一句话小结:
1、已知矩形的面积是a,求用斜二测画法得到的直观图的面积。
问题拓展
2、如图,一个水平放置的平面图形的斜二测直观图是一个等腰梯形,它的底角为45度,两腰和上底边长均为1,求这个平面图形的面积,并说明它是什么图形。
A’
B’
C’
D’
X’
y’
1
1
A
B
C
D
1
2
问题拓展
(二)空间几何体的直观图的画法
x
y
z
1350
x
O
y
z
x
y
z
A
B
C
D
A’
B’
D’
C’
D
C
A’
D’
C’
A
B
B’
例3 .画棱长为2cm的正方体的直观图
总结:画空间图形(柱体、锥体)的直观图的步骤:
建系
画一个底面
画侧棱
成 图
课后探索1:画正三棱柱ABC-A’B’C’的直观图,使它的底面是边长为2cm的正三角形,
高度是3cm.
课后探索2:画三棱锥的直观图,使它的底面是腰长为a的等腰直角三角形,过直角顶点的侧棱长为a,且垂直于底面.
例1、已知:
画出过A、B、C三点的平面 的交线
A
C
B
(1)
D
画截面问题
A
C
B
(2)
A
C
B
(3)
D
D
E
F
例2:如图,P,Q,R分别是空间四边形ABCD的边AB,AD,BC上的点,且PQ与BD不平行,试画出平面PQR与平面BCD的交线.
E
F
A
B
A
F
E
E
F
E
F
G
H
