沪教版(上海)数学高三上册-15.1多面体课件(共14张PPT)
文档属性
| 名称 | 沪教版(上海)数学高三上册-15.1多面体课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 127.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 00:00:00 | ||
图片预览


文档简介
一、多面体
1. 由若干个平面多边形围成的封闭体叫做多面体。
×
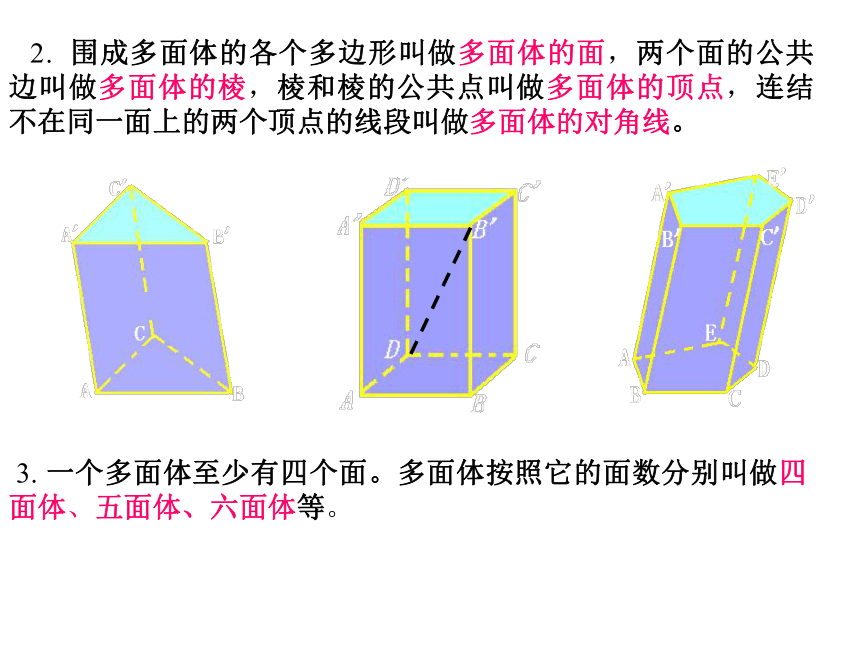
2. 围成多面体的各个多边形叫做多面体的面,两个面的公共边叫做多面体的棱,棱和棱的公共点叫做多面体的顶点,连结不在同一面上的两个顶点的线段叫做多面体的对角线。
3. 一个多面体至少有四个面。多面体按照它的面数分别叫做四面体、五面体、六面体等。
二、棱柱的概念
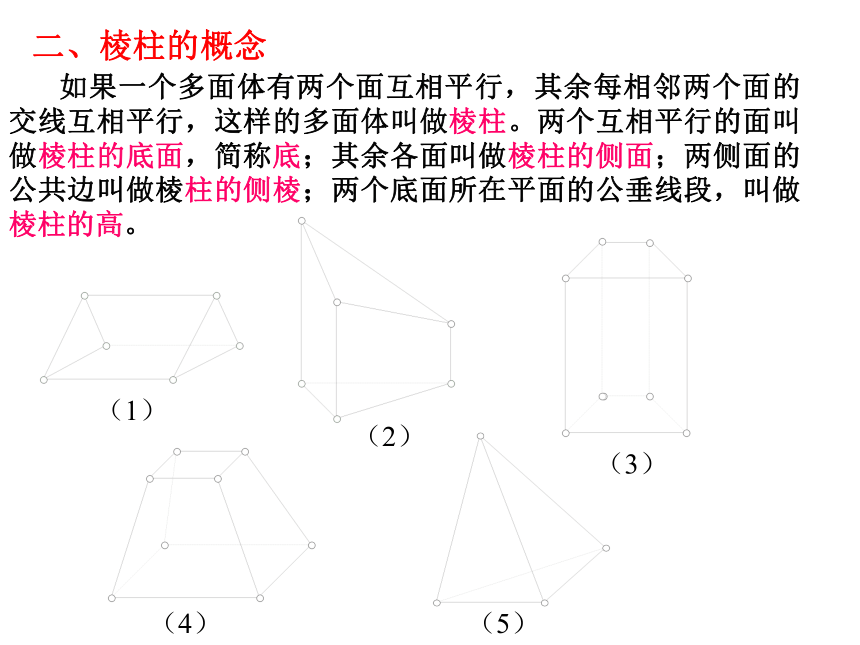
如果一个多面体有两个面互相平行,其余每相邻两个面的交线互相平行,这样的多面体叫做棱柱。两个互相平行的面叫做棱柱的底面,简称底;其余各面叫做棱柱的侧面;两侧面的公共边叫做棱柱的侧棱;两个底面所在平面的公垂线段,叫做棱柱的高。
(1)
(2)
(3)
(4)
(5)
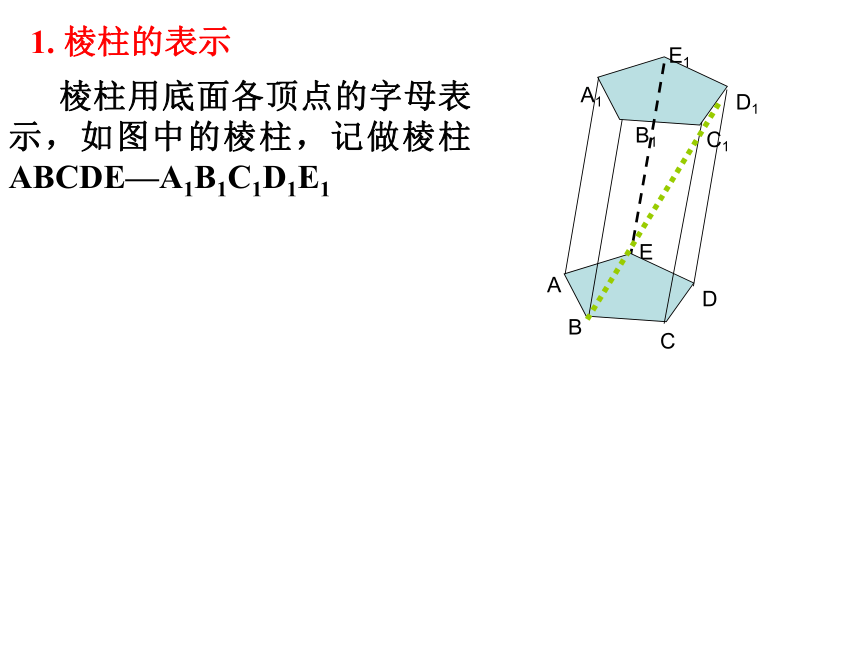
1. 棱柱的表示
棱柱用底面各顶点的字母表示,如图中的棱柱,记做棱柱ABCDE—A1B1C1D1E1
A
B
C
D
E
A1
B1
C1
E1
D1
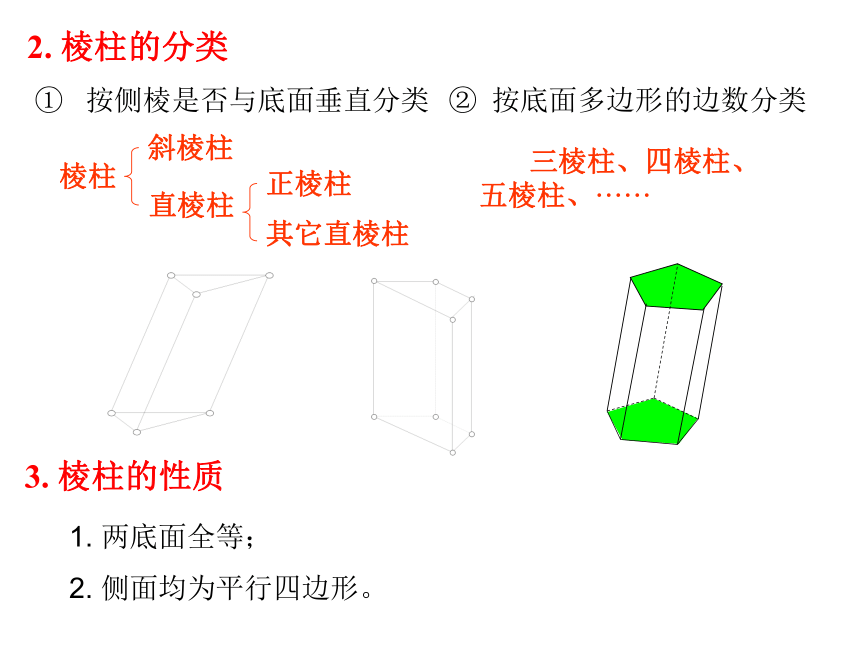
2. 棱柱的分类
按侧棱是否与底面垂直分类
棱柱
斜棱柱
直棱柱
正棱柱
其它直棱柱
按底面多边形的边数分类
三棱柱、四棱柱、
五棱柱、······
3. 棱柱的性质
1. 两底面全等;
2. 侧面均为平行四边形。
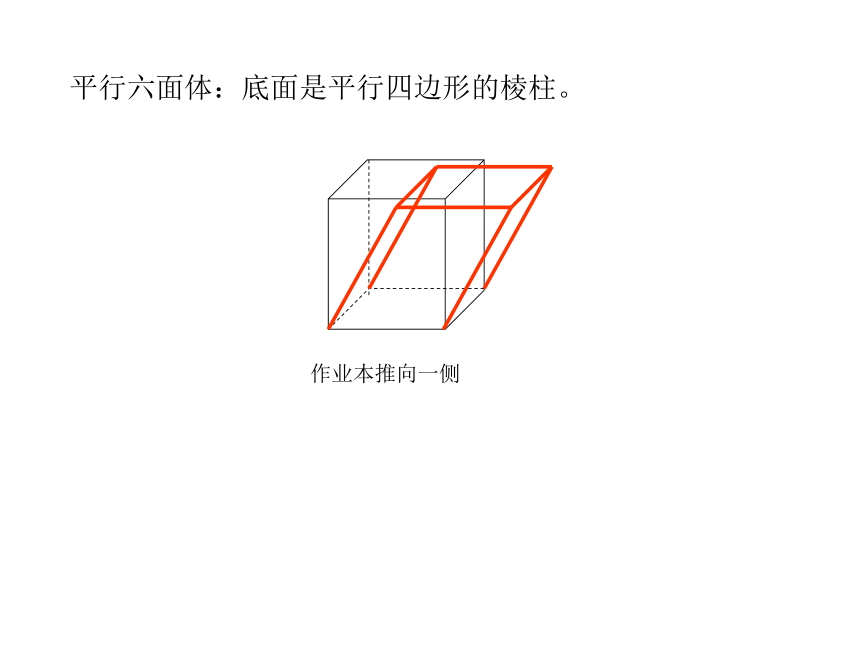
作业本推向一侧
平行六面体:底面是平行四边形的棱柱。
例1. 集合A={四棱柱},B={直四棱柱},C={正四棱柱},D={平行六面体},E={长方体}, F={正方体}。用文氏图表示以上集合之间的关系。
例2. 判断真假:
1. 侧棱与底面两条棱垂直的棱柱为直 棱柱。
2. 相邻侧面互相垂直的棱柱为直棱柱。
有一个面是多边形其余各面是三角形,这个多面体是棱锥吗?
如果一个多面体的一个面是多边形,其余各面都是有一个公共顶点的三角形,那么这个多面体就叫棱锥。
三、棱锥的概念
底面
侧面:有公共顶点的各三角形面
底面(底):余下的那个多边形
侧棱:两个相邻侧面的公共边
顶点:各侧面的公共点
高:顶点到底面的垂线段(距离)
顶点
侧棱
高
侧面
S
A
B
C
D
E
O
S
A
B
C
D
1. 棱锥的表示
棱锥S-ABCD
按底面多边形的边数:三棱锥、四棱锥、……
2. 棱锥的分类:
正棱锥
正棱锥
(2)顶点在底面上 的 射影是底面的中心
O
A
B
C
S
D
(1)底面是正多边形
A
A1
.
.
S
B
C
D
E
H
H1
B1
C1
D1
E1
如果棱锥被平行于底面的平面所截,那么所得的截面与底面相似,截面面积与底面面积的比等于顶点到截面的距离与棱锥的高的平方比。
3. 棱锥的性质
例3. 写出“底面是正三角形,顶点与底面中心的连线垂直于底面的三棱锥是正三棱锥”的等价命题。
1. 由若干个平面多边形围成的封闭体叫做多面体。
×
2. 围成多面体的各个多边形叫做多面体的面,两个面的公共边叫做多面体的棱,棱和棱的公共点叫做多面体的顶点,连结不在同一面上的两个顶点的线段叫做多面体的对角线。
3. 一个多面体至少有四个面。多面体按照它的面数分别叫做四面体、五面体、六面体等。
二、棱柱的概念
如果一个多面体有两个面互相平行,其余每相邻两个面的交线互相平行,这样的多面体叫做棱柱。两个互相平行的面叫做棱柱的底面,简称底;其余各面叫做棱柱的侧面;两侧面的公共边叫做棱柱的侧棱;两个底面所在平面的公垂线段,叫做棱柱的高。
(1)
(2)
(3)
(4)
(5)
1. 棱柱的表示
棱柱用底面各顶点的字母表示,如图中的棱柱,记做棱柱ABCDE—A1B1C1D1E1
A
B
C
D
E
A1
B1
C1
E1
D1
2. 棱柱的分类
按侧棱是否与底面垂直分类
棱柱
斜棱柱
直棱柱
正棱柱
其它直棱柱
按底面多边形的边数分类
三棱柱、四棱柱、
五棱柱、······
3. 棱柱的性质
1. 两底面全等;
2. 侧面均为平行四边形。
作业本推向一侧
平行六面体:底面是平行四边形的棱柱。
例1. 集合A={四棱柱},B={直四棱柱},C={正四棱柱},D={平行六面体},E={长方体}, F={正方体}。用文氏图表示以上集合之间的关系。
例2. 判断真假:
1. 侧棱与底面两条棱垂直的棱柱为直 棱柱。
2. 相邻侧面互相垂直的棱柱为直棱柱。
有一个面是多边形其余各面是三角形,这个多面体是棱锥吗?
如果一个多面体的一个面是多边形,其余各面都是有一个公共顶点的三角形,那么这个多面体就叫棱锥。
三、棱锥的概念
底面
侧面:有公共顶点的各三角形面
底面(底):余下的那个多边形
侧棱:两个相邻侧面的公共边
顶点:各侧面的公共点
高:顶点到底面的垂线段(距离)
顶点
侧棱
高
侧面
S
A
B
C
D
E
O
S
A
B
C
D
1. 棱锥的表示
棱锥S-ABCD
按底面多边形的边数:三棱锥、四棱锥、……
2. 棱锥的分类:
正棱锥
正棱锥
(2)顶点在底面上 的 射影是底面的中心
O
A
B
C
S
D
(1)底面是正多边形
A
A1
.
.
S
B
C
D
E
H
H1
B1
C1
D1
E1
如果棱锥被平行于底面的平面所截,那么所得的截面与底面相似,截面面积与底面面积的比等于顶点到截面的距离与棱锥的高的平方比。
3. 棱锥的性质
例3. 写出“底面是正三角形,顶点与底面中心的连线垂直于底面的三棱锥是正三棱锥”的等价命题。
