沪教版(上海)数学高三上册-15.3 球的体积公式解读 课件(共16张PPT)
文档属性
| 名称 | 沪教版(上海)数学高三上册-15.3 球的体积公式解读 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 381.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 00:00:00 | ||
图片预览






文档简介
--球的体积公式解读--
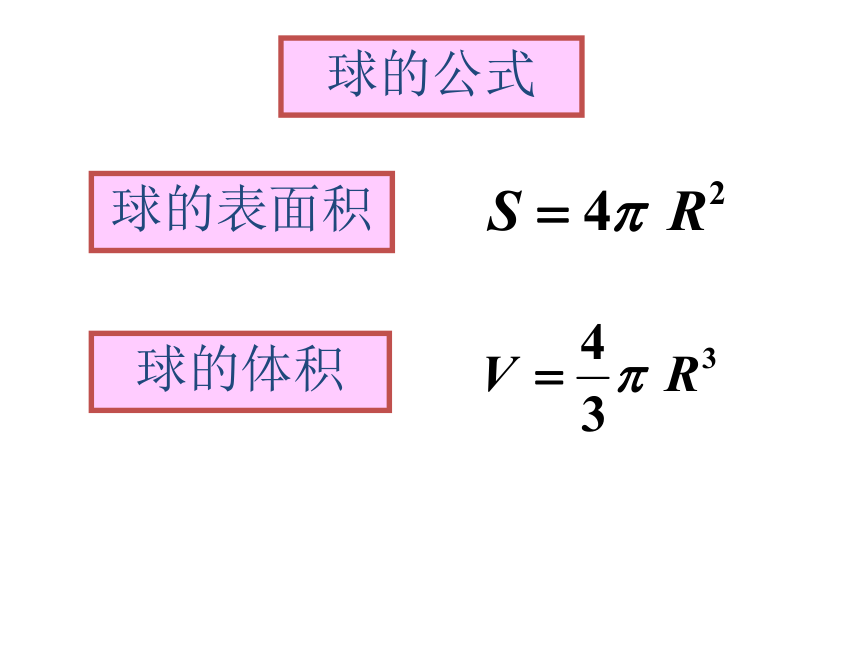
球的公式
球的体积
球的表面积
学习球的知识要注意和圆的有关指示结合起来.所以我们先来回忆圆面积计算公式的导出方法.
我们把一个半径为R的圆分成若干等分,然后如上图重新拼接起来,把一个圆近似的看成是边长分别是
解读一:极限求解
当所分份数不断增加时,精确程度就越来越高;当份数无穷大时,就得到了圆的面积公式.
即先把半球分割成n部分,再求出每一部分的近似体积,并将这些近似值相加,得出半球的近似体积,最后考虑n变为无穷大的情形,由半球的近似体积推出准确体积.
分割
求近似和
化为准确和
下面我们就运用上述方法导出球的体积公式
问题:已知球的半径为R,用R表示球的体积.
A
O
B2
C2
A
O
B1
将 上 半 球 进 行 n 等 分
O
R
O
解读二:表面积求解
第一步:分割
球面被分割成n个网格,表面积分别为:
则球的表面积:
则球的体积为:
O
O
第二步:求近似和
由第一步得:
O
O
第三步:化为准确和
如果网格分的越细,则: “小锥体”就越接近小棱锥
O
R
?
高等于底面半径的旋转体体积对比
解读三:祖暅原理求解
练习:已知椭圆的标准方程为
将此椭圆绕y轴旋转一周后,得一橄榄状的几何体,利用祖暅原理求其体积。
例1:三个球的半径之比为1:2:3,那么最大的球的体积是其余两个球体积和的________倍
例2:棱长为1的正方体的外接球A、内切球B及正方体各棱都相切的球C,则球A、球B、球C的体积比为______
小结
球的公式
球的体积
球的表面积
学习球的知识要注意和圆的有关指示结合起来.所以我们先来回忆圆面积计算公式的导出方法.
我们把一个半径为R的圆分成若干等分,然后如上图重新拼接起来,把一个圆近似的看成是边长分别是
解读一:极限求解
当所分份数不断增加时,精确程度就越来越高;当份数无穷大时,就得到了圆的面积公式.
即先把半球分割成n部分,再求出每一部分的近似体积,并将这些近似值相加,得出半球的近似体积,最后考虑n变为无穷大的情形,由半球的近似体积推出准确体积.
分割
求近似和
化为准确和
下面我们就运用上述方法导出球的体积公式
问题:已知球的半径为R,用R表示球的体积.
A
O
B2
C2
A
O
B1
将 上 半 球 进 行 n 等 分
O
R
O
解读二:表面积求解
第一步:分割
球面被分割成n个网格,表面积分别为:
则球的表面积:
则球的体积为:
O
O
第二步:求近似和
由第一步得:
O
O
第三步:化为准确和
如果网格分的越细,则: “小锥体”就越接近小棱锥
O
R
?
高等于底面半径的旋转体体积对比
解读三:祖暅原理求解
练习:已知椭圆的标准方程为
将此椭圆绕y轴旋转一周后,得一橄榄状的几何体,利用祖暅原理求其体积。
例1:三个球的半径之比为1:2:3,那么最大的球的体积是其余两个球体积和的________倍
例2:棱长为1的正方体的外接球A、内切球B及正方体各棱都相切的球C,则球A、球B、球C的体积比为______
小结
