沪教版(上海)数学高三上册-15.3 锥体的体积(1) 课件(18张PPT)
文档属性
| 名称 | 沪教版(上海)数学高三上册-15.3 锥体的体积(1) 课件(18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 303.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 00:00:00 | ||
图片预览


文档简介
15.5-2锥体的体积(1)
1.祖暅原理
夹在两个平行平面间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.
复习
棱柱的体积等于它的底面积s和高h的积。
V棱柱= sh
2.棱柱体积
“夫叠棊成立积,缘幂势既同,则积不容异”.
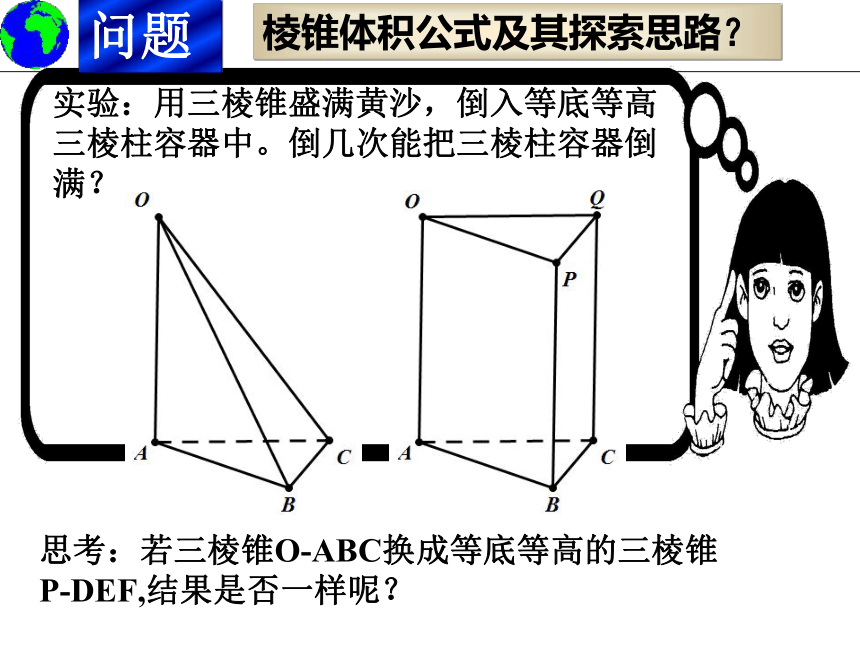
棱锥体积公式及其探索思路?
问题
实验:用三棱锥盛满黄沙,倒入等底等高三棱柱容器中。倒几次能把三棱柱容器倒满?
思考:若三棱锥O-ABC换成等底等高的三棱锥P-DEF,结果是否一样呢?
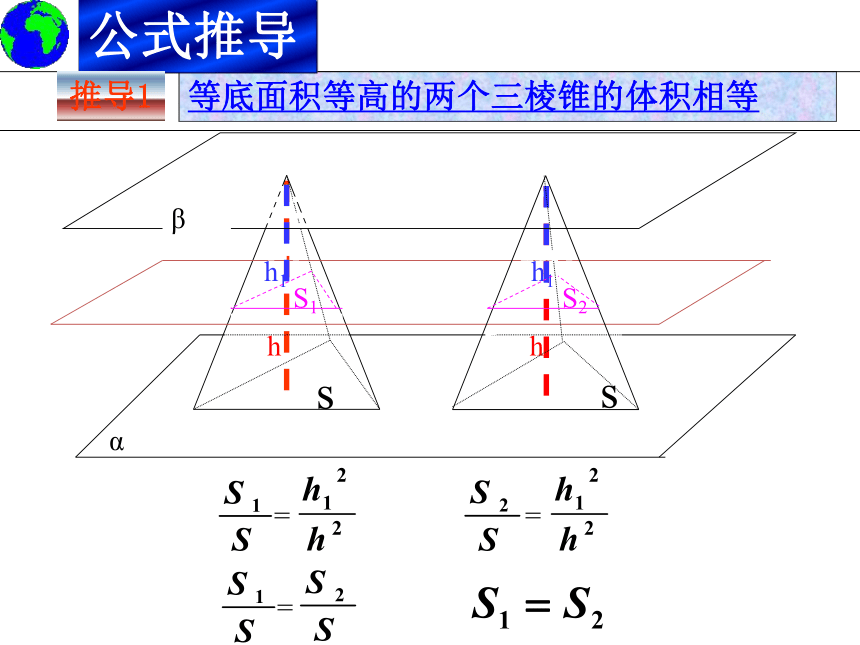
等底面积等高的两个三棱锥的体积相等
公式推导
推导1
=
=
=
α
s
h
s
h
S1
S2
h1
h1
β
公式推导
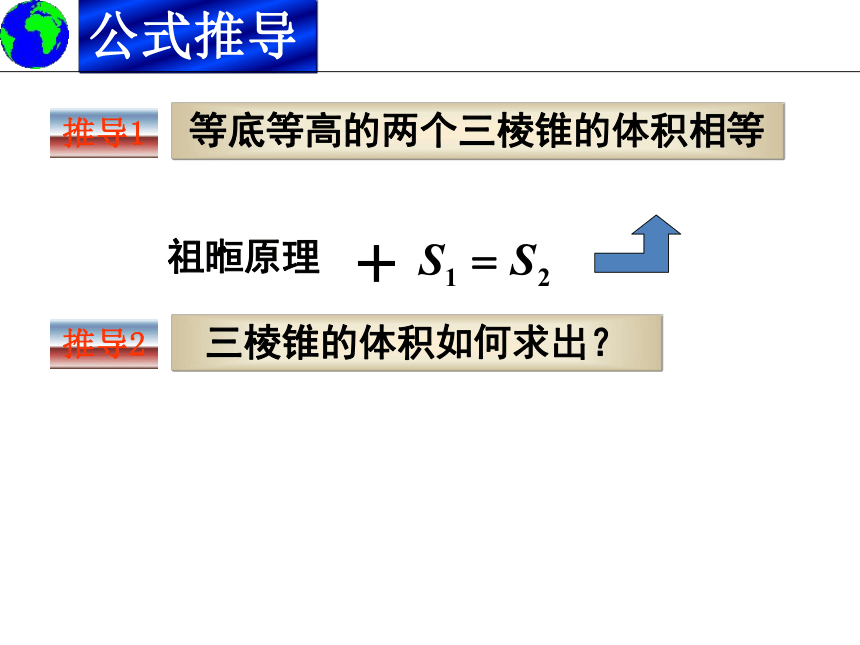
等底等高的两个三棱锥的体积相等
推导1
+
祖暅原理
推导2
三棱锥的体积如何求出?
公式推导
推导2
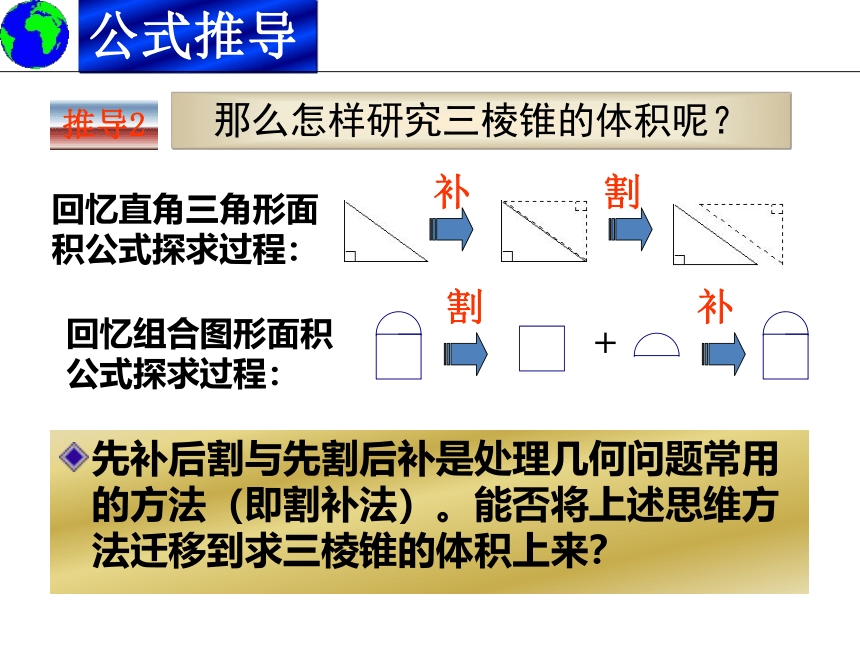
那么怎样研究三棱锥的体积呢?
回忆直角三角形面积公式探求过程:
补
割
回忆组合图形面积公式探求过程:
+
割
补
先补后割与先割后补是处理几何问题常用的方法(即割补法)。能否将上述思维方法迁移到求三棱锥的体积上来?
公式推导
A
B
C
A′
B′
C′
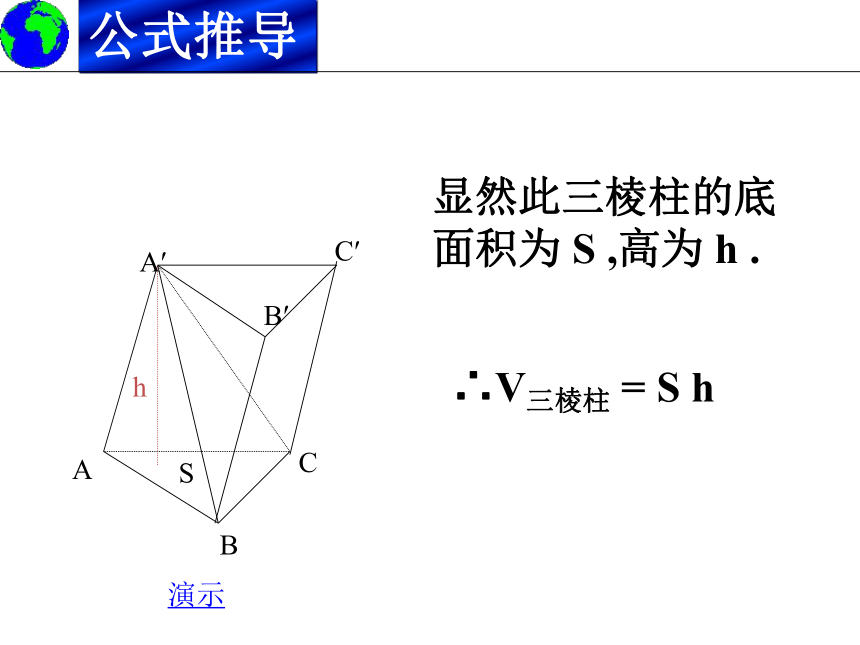
显然此三棱柱的底面积为 S ,高为 h .
∴V三棱柱 = S h
h
S
演示
公式推导
1
2
3
A
B
C
A′
B′
C′
显然此三棱柱的底面积为 S ,高为 h .
∴V三棱柱 = S h
公式推导
1
2
3
A
B
C
A′
B′
C′
显然此三棱柱的底面积为 S ,高为 h .
∴V三棱柱 = S h
1
2
A
B
B′
C
A′
B′
3
C
A′
C′
B′
3
C
A′
C′
B′
3
C
A′
C′
B′
3
C
A′
′
公式推导
显然此三棱柱的底面积为 S ,高为 h .
∴V三棱柱 = S h
1
A
B
C
A′
B′
3
C
A′
C′
B
B′
C
A′
2
B
B′
C
A′
2
B
B′
C
A′
2
B
C
A′
B
B′
C
A′
2
公式推导
A
1
B
C
A′
B
B′
C
A′
2
B
B′
C
A′
2
B
B′
C
A′
2
B
C
A′
B
B′
C
A′
2
B′
3
C
A′
C′
公式推导
分析.∵ S △ A’AB (面1) = S △ A’B’B (面2) (底 )
即 V1= V2
同理可证 V2= V3 ( 怎证 ? )
C点到面 A’AB (面1)的距离等于C点到面 A’B’B(面2)的距离(高)
(用 S△B B’ C (面4) = S△ C’ B’ C (面3) 可证 )
∴ V1= V2= V3
∴ V三棱锥C - A’ AB= V三棱锥C -A’B’B
因此 V1= V2= V3 = V三 棱柱
= Sh
1
2
3
A
B
C
A′
B′
C′
h
S
即 V三棱锥A’-- ABC = S h
公式推导
4
定理:
三棱锥 V三棱锥=
Sh (底面积为S ,高为 h)
推导3
三棱锥的体积问题已经解决了,那么一般棱锥的体积如何呢?
公式推导
四棱锥的体积?N棱锥的体积?
A
0
D
B
C
P
公式应用
例1、求棱长都为a的正四棱锥的体积 。
在棱长为a的正方体 中,
(1)求三棱锥 的体积;
(2)求三棱锥 的体积;
例2:
公式应用
解:
课堂小结
知识方面
本节课学习了利用祖暅原理、割补法获得了棱锥的体积公式,并初步体会棱锥体积公式的应用;
思维能力方面
体会到联想、类比、猜想、证明等合情推理及逻辑推理的方法在探索新知识方面的重要作用。
下课
1.祖暅原理
夹在两个平行平面间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.
复习
棱柱的体积等于它的底面积s和高h的积。
V棱柱= sh
2.棱柱体积
“夫叠棊成立积,缘幂势既同,则积不容异”.
棱锥体积公式及其探索思路?
问题
实验:用三棱锥盛满黄沙,倒入等底等高三棱柱容器中。倒几次能把三棱柱容器倒满?
思考:若三棱锥O-ABC换成等底等高的三棱锥P-DEF,结果是否一样呢?
等底面积等高的两个三棱锥的体积相等
公式推导
推导1
=
=
=
α
s
h
s
h
S1
S2
h1
h1
β
公式推导
等底等高的两个三棱锥的体积相等
推导1
+
祖暅原理
推导2
三棱锥的体积如何求出?
公式推导
推导2
那么怎样研究三棱锥的体积呢?
回忆直角三角形面积公式探求过程:
补
割
回忆组合图形面积公式探求过程:
+
割
补
先补后割与先割后补是处理几何问题常用的方法(即割补法)。能否将上述思维方法迁移到求三棱锥的体积上来?
公式推导
A
B
C
A′
B′
C′
显然此三棱柱的底面积为 S ,高为 h .
∴V三棱柱 = S h
h
S
演示
公式推导
1
2
3
A
B
C
A′
B′
C′
显然此三棱柱的底面积为 S ,高为 h .
∴V三棱柱 = S h
公式推导
1
2
3
A
B
C
A′
B′
C′
显然此三棱柱的底面积为 S ,高为 h .
∴V三棱柱 = S h
1
2
A
B
B′
C
A′
B′
3
C
A′
C′
B′
3
C
A′
C′
B′
3
C
A′
C′
B′
3
C
A′
′
公式推导
显然此三棱柱的底面积为 S ,高为 h .
∴V三棱柱 = S h
1
A
B
C
A′
B′
3
C
A′
C′
B
B′
C
A′
2
B
B′
C
A′
2
B
B′
C
A′
2
B
C
A′
B
B′
C
A′
2
公式推导
A
1
B
C
A′
B
B′
C
A′
2
B
B′
C
A′
2
B
B′
C
A′
2
B
C
A′
B
B′
C
A′
2
B′
3
C
A′
C′
公式推导
分析.∵ S △ A’AB (面1) = S △ A’B’B (面2) (底 )
即 V1= V2
同理可证 V2= V3 ( 怎证 ? )
C点到面 A’AB (面1)的距离等于C点到面 A’B’B(面2)的距离(高)
(用 S△B B’ C (面4) = S△ C’ B’ C (面3) 可证 )
∴ V1= V2= V3
∴ V三棱锥C - A’ AB= V三棱锥C -A’B’B
因此 V1= V2= V3 = V三 棱柱
= Sh
1
2
3
A
B
C
A′
B′
C′
h
S
即 V三棱锥A’-- ABC = S h
公式推导
4
定理:
三棱锥 V三棱锥=
Sh (底面积为S ,高为 h)
推导3
三棱锥的体积问题已经解决了,那么一般棱锥的体积如何呢?
公式推导
四棱锥的体积?N棱锥的体积?
A
0
D
B
C
P
公式应用
例1、求棱长都为a的正四棱锥的体积 。
在棱长为a的正方体 中,
(1)求三棱锥 的体积;
(2)求三棱锥 的体积;
例2:
公式应用
解:
课堂小结
知识方面
本节课学习了利用祖暅原理、割补法获得了棱锥的体积公式,并初步体会棱锥体积公式的应用;
思维能力方面
体会到联想、类比、猜想、证明等合情推理及逻辑推理的方法在探索新知识方面的重要作用。
下课
