沪教版(上海)数学高三上册-16.5 二项式系数与杨辉三角形 课件(62张PPT)
文档属性
| 名称 | 沪教版(上海)数学高三上册-16.5 二项式系数与杨辉三角形 课件(62张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 12:17:21 | ||
图片预览










文档简介
二项式系数与杨辉三角形
Binomial Coefficients & Pascal’s Triangle
上海市位育中学
龚菲
知识回顾
二项式定理(Binomial Theorem)
存款份
二项式系数(Binomial Coefficients)
上海市位育中学
龚菲
杨辉三角形的构成
上海市位育中学
龚菲
杨辉三角形的构成
上海市位育中学
龚菲
杨辉
三角形
上海市位育中学
龚菲
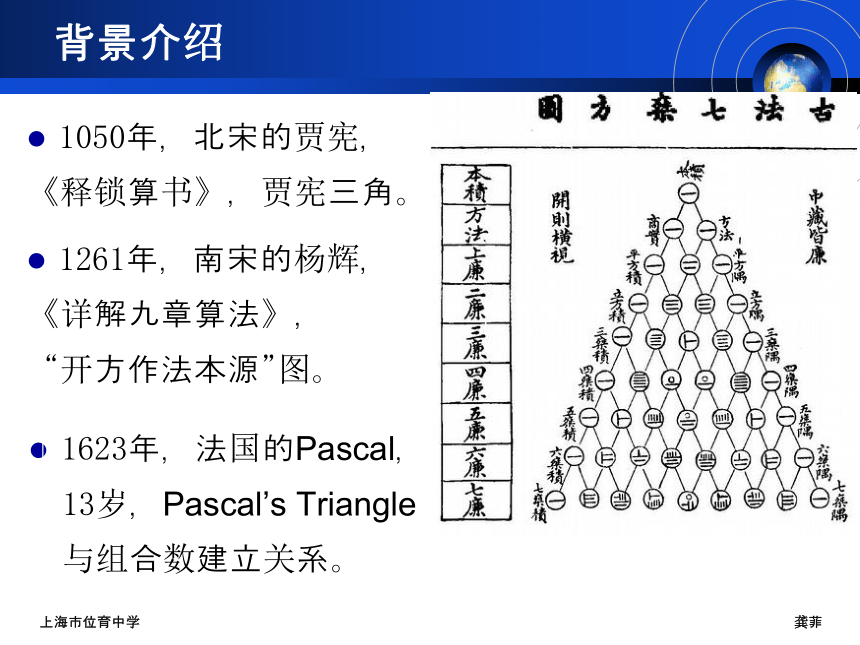
背景介绍
1623年,法国的Pascal,
13岁,Pascal’s Triangle
与组合数建立关系。
1050年,北宋的贾宪,
《释锁算书》,贾宪三角。
1261年,南宋的杨辉,
《详解九章算法》,
“开方作法本源”图。
上海市位育中学
高尔顿板
龚菲
上海市位育中学
高尔顿板模拟演示
龚菲
上海市位育中学
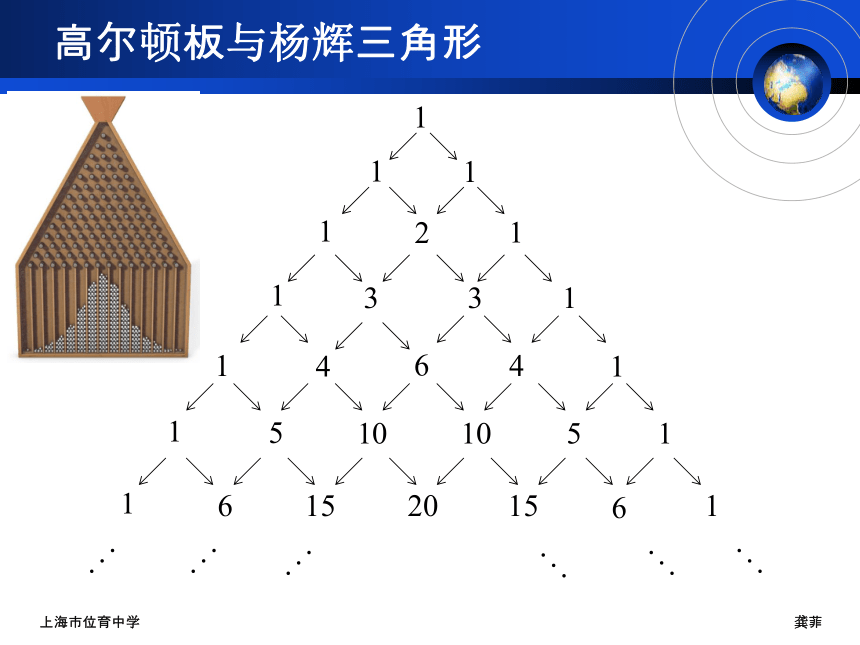
高尔顿板与杨辉三角形
龚菲
上海市位育中学
龚菲
二项式系数与杨辉三角形
上海市位育中学
龚菲
二项式系数与杨辉三角形
上海市位育中学
龚菲
二项式系数与杨辉三角形
上海市位育中学
龚菲
二项式系数与杨辉三角形
上海市位育中学
龚菲
二项式系数与杨辉三角形
上海市位育中学
龚菲
二项式系数与杨辉三角形
上海市位育中学
龚菲
二项式系数与杨辉三角形
上海市位育中学
龚菲
二项式系数与杨辉三角形
上海市位育中学
龚菲
二项式系数与杨辉三角形
上海市位育中学
龚菲
二项式系数与杨辉三角形
上海市位育中学
龚菲
杨辉三角形的特征
上海市位育中学
龚菲
杨辉三角形的特征
性质1:
左右斜边上都是1
上海市位育中学
龚菲
二项式系数的性质1
性质1:
左右斜边上都是1
上海市位育中学
龚菲
二项式系数的性质1
性质1:
????0=????????=1
?
上海市位育中学
龚菲
杨辉三角形的特征
上海市位育中学
龚菲
杨辉三角形的特征
性质2:
左右次斜边上
是连续整数
上海市位育中学
龚菲
二项式系数的性质2
性质2:
左右次斜边上
是连续整数
上海市位育中学
龚菲
二项式系数的性质2
上海市位育中学
龚菲
二项式系数的性质2
性质2:
????1=?????????1=????
?
上海市位育中学
龚菲
杨辉三角形的特征
上海市位育中学
龚菲
杨辉三角形的特征
性质3:
左右对称性
上海市位育中学
龚菲
二项式系数的性质3
性质3:
左右对称性
二项式系数的性质3
上海市位育中学
龚菲
二项式系数的性质3
上海市位育中学
龚菲
性质3:????????=?????????????
?
上海市位育中学
龚菲
杨辉三角形的特征
上海市位育中学
杨辉三角形的特征
龚菲
性质4:
每个数等于它上方两数之和
上海市位育中学
龚菲
二项式系数的性质4
性质4:
每个数等于它上方两数之和
上海市位育中学
龚菲
二项式系数的性质4
上海市位育中学
龚菲
二项式系数的性质4
性质4:
?????????1+????????
=????+1????
?
上海市位育中学
龚菲
如何构成杨辉三角形?
存款份
运用二项式定理。
上海市位育中学
龚菲
二项式系数的性质1
性质1:
左右斜边上都是1
上海市位育中学
龚菲
二项式系数的性质2
性质2:
左右次斜边上
是连续整数
上海市位育中学
龚菲
二项式系数的性质3
性质3:
左右对称性
上海市位育中学
龚菲
二项式系数的性质4
性质4:
每个数等于它上方两数之和
上海市位育中学
龚菲
二项式系数的性质
存款份
性质1:
????0=????????=1
?
性质2:
?????????1=?????????1=????
?
性质4:
??????????1+????????=????+1????
?
性质3:
????????=?????????????
?
理论证明
上海市位育中学
龚菲
二项式系数的性质的理论证明
性质1:
????0=????????=1
?
证明:
????0=????!0!?????0!=????!????!=1
?
?????????=????!????!?????????!=????!????!=1
?
上海市位育中学
龚菲
二项式系数的性质的理论证明
????1=????!1!?????1!=?????????1!?????1!=n
?
性质2:
????1=?????????1=????
?
?????????1=????!?????1!?????????+1!=?????????1!?????1!=n
?
证明:
上海市位育中学
龚菲
二项式系数的性质的理论证明
????????=????!????!?????????!=????!?????????!?????????+????!=?????????????
?
性质3:
????????=?????????????
?
证明:
上海市位育中学
龚菲
二项式系数的性质的理论证明
性质4:
?????????1+????????=????+1????
?
上海市位育中学
龚菲
杨辉三角形(Pascal’s Triangle)
横看成岭侧成峰
远近高低各不同
+ + + + + +
+ + + + +
+ + + +
+ + +
+ +
+
上海市位育中学
龚菲
横向和
1
2
4
8
16
32
64
=
=
=
=
=
=
=
20
?
=
=
=
=
=
=
=
21
?
22
?
23
?
24
?
25
?
26
?
第一行
第三行
第五行
上海市位育中学
龚菲
横向和
2????
?
第????+1行
?
上海市位育中学
龚菲
横向和
性质5:
????0+????1+????2+…+?????????1+????????=2????
?
请理论证明性质5
提示2:在????+????????中选取合适的????和????的值。
?
提示1:运用二项式定理展开。
上海市位育中学
龚菲
斜线和(一)
上海市位育中学
龚菲
斜线和(一)
+
?
=
+
?
+
?
+
?
=
+
?
+
?
=
上海市位育中学
斜线和(一)
+
?
+
?
+
?
=
+
?
+
?
+
?
=
…
?
+
?
性质6:
????????+????+1????+????+2????+…+?????1????=????????+1
?
龚菲
上海市位育中学
斜线和(二)
性质6:
????????+????+1????+????+2????+…+?????1????=????????+1
?
????0
?
性质7:
龚菲
设????=1,????=5
?
10
?
+????+11
?
+????+22
?
+…+
?
?????1??????????1
?
=??????????????1
?
+21
?
+32
?
+43
?
=53
?
上海市位育中学
斜线和(二)
????0+????+11+????+22+…+?????1??????????1=??????????????1
?
性质7:
龚菲
上海市位育中学
龚菲
斜线和(二)
+
?
+
?
+
?
=
10+21+32+43=53
?
上海市位育中学
龚菲
斜线和(二)
上海市位育中学
Fibonnaci数列
????1=1,????2=1
?
????1=1????????????????????5=5
????2=1???????????????????6=8
????3=2???????????????????7=13
????4=3???????????????????8=21
?
龚菲
????????=?????????1+?????????2??????≥3
?
上海市位育中学
龚菲
斜线和(三)
1
=
?
1
2
3
5
8
13
21
=
?
=
?
=
?
=
?
=
?
=
?
=
?
上海市位育中学
龚菲
世事
洞明
皆数学
处处
留心
是学问
有心人
Binomial Coefficients & Pascal’s Triangle
上海市位育中学
龚菲
知识回顾
二项式定理(Binomial Theorem)
存款份
二项式系数(Binomial Coefficients)
上海市位育中学
龚菲
杨辉三角形的构成
上海市位育中学
龚菲
杨辉三角形的构成
上海市位育中学
龚菲
杨辉
三角形
上海市位育中学
龚菲
背景介绍
1623年,法国的Pascal,
13岁,Pascal’s Triangle
与组合数建立关系。
1050年,北宋的贾宪,
《释锁算书》,贾宪三角。
1261年,南宋的杨辉,
《详解九章算法》,
“开方作法本源”图。
上海市位育中学
高尔顿板
龚菲
上海市位育中学
高尔顿板模拟演示
龚菲
上海市位育中学
高尔顿板与杨辉三角形
龚菲
上海市位育中学
龚菲
二项式系数与杨辉三角形
上海市位育中学
龚菲
二项式系数与杨辉三角形
上海市位育中学
龚菲
二项式系数与杨辉三角形
上海市位育中学
龚菲
二项式系数与杨辉三角形
上海市位育中学
龚菲
二项式系数与杨辉三角形
上海市位育中学
龚菲
二项式系数与杨辉三角形
上海市位育中学
龚菲
二项式系数与杨辉三角形
上海市位育中学
龚菲
二项式系数与杨辉三角形
上海市位育中学
龚菲
二项式系数与杨辉三角形
上海市位育中学
龚菲
二项式系数与杨辉三角形
上海市位育中学
龚菲
杨辉三角形的特征
上海市位育中学
龚菲
杨辉三角形的特征
性质1:
左右斜边上都是1
上海市位育中学
龚菲
二项式系数的性质1
性质1:
左右斜边上都是1
上海市位育中学
龚菲
二项式系数的性质1
性质1:
????0=????????=1
?
上海市位育中学
龚菲
杨辉三角形的特征
上海市位育中学
龚菲
杨辉三角形的特征
性质2:
左右次斜边上
是连续整数
上海市位育中学
龚菲
二项式系数的性质2
性质2:
左右次斜边上
是连续整数
上海市位育中学
龚菲
二项式系数的性质2
上海市位育中学
龚菲
二项式系数的性质2
性质2:
????1=?????????1=????
?
上海市位育中学
龚菲
杨辉三角形的特征
上海市位育中学
龚菲
杨辉三角形的特征
性质3:
左右对称性
上海市位育中学
龚菲
二项式系数的性质3
性质3:
左右对称性
二项式系数的性质3
上海市位育中学
龚菲
二项式系数的性质3
上海市位育中学
龚菲
性质3:????????=?????????????
?
上海市位育中学
龚菲
杨辉三角形的特征
上海市位育中学
杨辉三角形的特征
龚菲
性质4:
每个数等于它上方两数之和
上海市位育中学
龚菲
二项式系数的性质4
性质4:
每个数等于它上方两数之和
上海市位育中学
龚菲
二项式系数的性质4
上海市位育中学
龚菲
二项式系数的性质4
性质4:
?????????1+????????
=????+1????
?
上海市位育中学
龚菲
如何构成杨辉三角形?
存款份
运用二项式定理。
上海市位育中学
龚菲
二项式系数的性质1
性质1:
左右斜边上都是1
上海市位育中学
龚菲
二项式系数的性质2
性质2:
左右次斜边上
是连续整数
上海市位育中学
龚菲
二项式系数的性质3
性质3:
左右对称性
上海市位育中学
龚菲
二项式系数的性质4
性质4:
每个数等于它上方两数之和
上海市位育中学
龚菲
二项式系数的性质
存款份
性质1:
????0=????????=1
?
性质2:
?????????1=?????????1=????
?
性质4:
??????????1+????????=????+1????
?
性质3:
????????=?????????????
?
理论证明
上海市位育中学
龚菲
二项式系数的性质的理论证明
性质1:
????0=????????=1
?
证明:
????0=????!0!?????0!=????!????!=1
?
?????????=????!????!?????????!=????!????!=1
?
上海市位育中学
龚菲
二项式系数的性质的理论证明
????1=????!1!?????1!=?????????1!?????1!=n
?
性质2:
????1=?????????1=????
?
?????????1=????!?????1!?????????+1!=?????????1!?????1!=n
?
证明:
上海市位育中学
龚菲
二项式系数的性质的理论证明
????????=????!????!?????????!=????!?????????!?????????+????!=?????????????
?
性质3:
????????=?????????????
?
证明:
上海市位育中学
龚菲
二项式系数的性质的理论证明
性质4:
?????????1+????????=????+1????
?
上海市位育中学
龚菲
杨辉三角形(Pascal’s Triangle)
横看成岭侧成峰
远近高低各不同
+ + + + + +
+ + + + +
+ + + +
+ + +
+ +
+
上海市位育中学
龚菲
横向和
1
2
4
8
16
32
64
=
=
=
=
=
=
=
20
?
=
=
=
=
=
=
=
21
?
22
?
23
?
24
?
25
?
26
?
第一行
第三行
第五行
上海市位育中学
龚菲
横向和
2????
?
第????+1行
?
上海市位育中学
龚菲
横向和
性质5:
????0+????1+????2+…+?????????1+????????=2????
?
请理论证明性质5
提示2:在????+????????中选取合适的????和????的值。
?
提示1:运用二项式定理展开。
上海市位育中学
龚菲
斜线和(一)
上海市位育中学
龚菲
斜线和(一)
+
?
=
+
?
+
?
+
?
=
+
?
+
?
=
上海市位育中学
斜线和(一)
+
?
+
?
+
?
=
+
?
+
?
+
?
=
…
?
+
?
性质6:
????????+????+1????+????+2????+…+?????1????=????????+1
?
龚菲
上海市位育中学
斜线和(二)
性质6:
????????+????+1????+????+2????+…+?????1????=????????+1
?
????0
?
性质7:
龚菲
设????=1,????=5
?
10
?
+????+11
?
+????+22
?
+…+
?
?????1??????????1
?
=??????????????1
?
+21
?
+32
?
+43
?
=53
?
上海市位育中学
斜线和(二)
????0+????+11+????+22+…+?????1??????????1=??????????????1
?
性质7:
龚菲
上海市位育中学
龚菲
斜线和(二)
+
?
+
?
+
?
=
10+21+32+43=53
?
上海市位育中学
龚菲
斜线和(二)
上海市位育中学
Fibonnaci数列
????1=1,????2=1
?
????1=1????????????????????5=5
????2=1???????????????????6=8
????3=2???????????????????7=13
????4=3???????????????????8=21
?
龚菲
????????=?????????1+?????????2??????≥3
?
上海市位育中学
龚菲
斜线和(三)
1
=
?
1
2
3
5
8
13
21
=
?
=
?
=
?
=
?
=
?
=
?
=
?
上海市位育中学
龚菲
世事
洞明
皆数学
处处
留心
是学问
有心人
