沪教版(上海)数学高三上册-16.5 二项式定理 课件(16张PPT)
文档属性
| 名称 | 沪教版(上海)数学高三上册-16.5 二项式定理 课件(16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 00:00:00 | ||
图片预览





文档简介
16.5 二项式定理
一、情景引入
1664年冬,牛顿研读沃利斯博士的《无穷算法》
牛顿思考
?
?
.
.
.
公元前3世纪《几何原本》卷2
公元50-100年的
《九章算术》第四卷内
13世纪杨辉在《详解九章算法》中有引用了“开方作法本源”图
二、数学史介绍
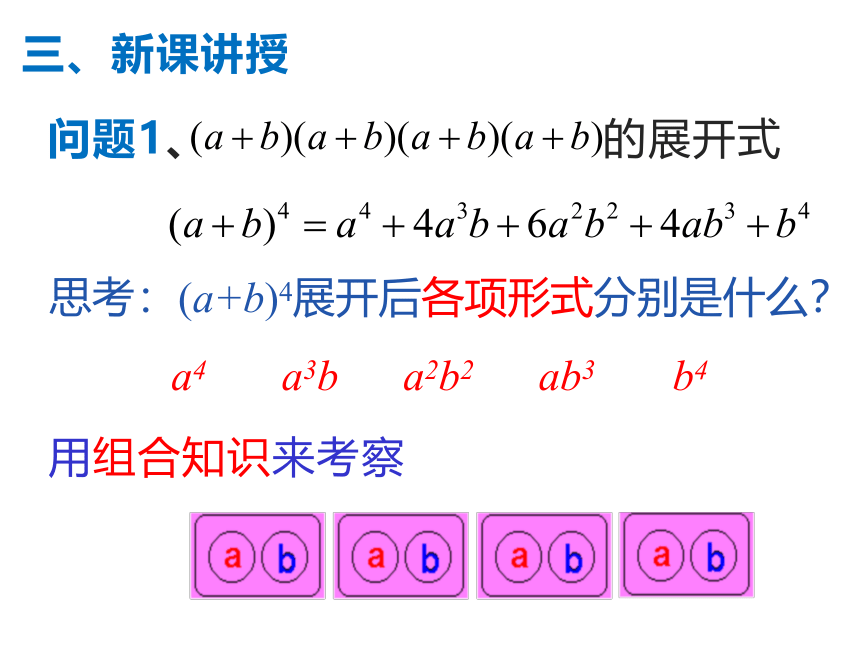
问题1、 的展开式
思考:(a+b)4展开后各项形式分别是什么?
a4 a3b a2b2 ab3 b4
三、新课讲授
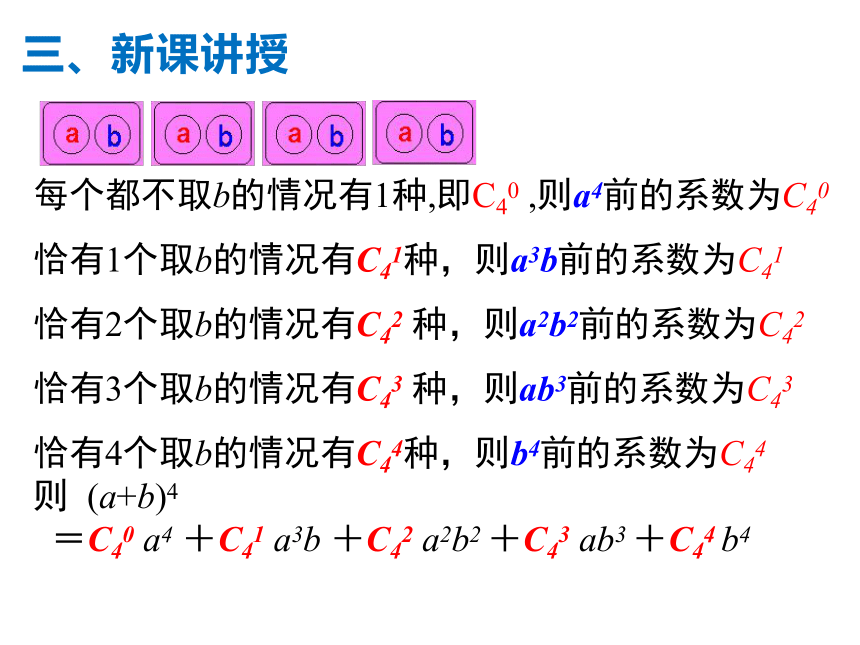
用组合知识来考察
每个都不取b的情况有1种,即C40 ,则a4前的系数为C40
恰有1个取b的情况有C41种,则a3b前的系数为C41
恰有2个取b的情况有C42 种,则a2b2前的系数为C42
恰有3个取b的情况有C43 种,则ab3前的系数为C43
恰有4个取b的情况有C44种,则b4前的系数为C44
则 (a+b)4
=C40 a4 +C41 a3b +C42 a2b2 +C43 ab3 +C44 b4
三、新课讲授
问题2、 的展开式
三、新课讲授
(用组合数表示出各项系数)
问题3、 的展开式
三、新课讲授
二项展开式定理
通项公式(第r+1项):
二项式系数:展开式中的系数
叫做二项式系数
每个都不取b的情况有1种,即Cn0 ,则an前的系数为Cn0
恰有1个取b的情况有Cn1种,则an-1b前的系数为Cn1
恰有2个取b的情况有Cn2 种,则an-2b2前的系数为Cn2
......
恰有r个取b的情况有Cnr 种,则an-rbr前的系数为Cnr
......
恰有n个取b的情况有Cnn 种,则bn前的系数为Cnn
二项展开式定理
三、新课讲授
提问:二项式定理展开式中项数、指数、系数的特点是什么?
(见例3)
①项数:共n+1项
顺序:注意正确选择a、b,其顺序不能更改!
②指数:
b的指数从0逐项递增到n,是升幂排列
a的指数从n逐项递减到0,是降幂排列
各项的次数都等于n,是关于a与b的齐次多项式
三、新课讲授
四、典型例题
例1、请写出 的展开式。
解:
四、典型例题
例2、求 的二项式展开式中的第6项。
解:
变式1、求 的二项式展开式中的
第6项的二项式系数。
解:
变式2、求 的二项式展开式中
的第6项的系数。
解:
四、典型例题
变式3、求 的二项式展开式中
的倒数第6项。
解:
例2、求 的二项式展开式中的第6项。
四、典型例题
例3、求 二项展开式中的常数项。
解:
五、拓展思考
*求证:
证明:
六、课堂小结
知识方面:二项式定理;
通项;
二项式系数;
思想方法:从特殊到一般;
七、学习情况反馈
自测1:求 的展开式。
自测2:求 的二项展开式中 项的系数。
自测3:求 的二项展开式中的常数项。
自测4:求证:
一、情景引入
1664年冬,牛顿研读沃利斯博士的《无穷算法》
牛顿思考
?
?
.
.
.
公元前3世纪《几何原本》卷2
公元50-100年的
《九章算术》第四卷内
13世纪杨辉在《详解九章算法》中有引用了“开方作法本源”图
二、数学史介绍
问题1、 的展开式
思考:(a+b)4展开后各项形式分别是什么?
a4 a3b a2b2 ab3 b4
三、新课讲授
用组合知识来考察
每个都不取b的情况有1种,即C40 ,则a4前的系数为C40
恰有1个取b的情况有C41种,则a3b前的系数为C41
恰有2个取b的情况有C42 种,则a2b2前的系数为C42
恰有3个取b的情况有C43 种,则ab3前的系数为C43
恰有4个取b的情况有C44种,则b4前的系数为C44
则 (a+b)4
=C40 a4 +C41 a3b +C42 a2b2 +C43 ab3 +C44 b4
三、新课讲授
问题2、 的展开式
三、新课讲授
(用组合数表示出各项系数)
问题3、 的展开式
三、新课讲授
二项展开式定理
通项公式(第r+1项):
二项式系数:展开式中的系数
叫做二项式系数
每个都不取b的情况有1种,即Cn0 ,则an前的系数为Cn0
恰有1个取b的情况有Cn1种,则an-1b前的系数为Cn1
恰有2个取b的情况有Cn2 种,则an-2b2前的系数为Cn2
......
恰有r个取b的情况有Cnr 种,则an-rbr前的系数为Cnr
......
恰有n个取b的情况有Cnn 种,则bn前的系数为Cnn
二项展开式定理
三、新课讲授
提问:二项式定理展开式中项数、指数、系数的特点是什么?
(见例3)
①项数:共n+1项
顺序:注意正确选择a、b,其顺序不能更改!
②指数:
b的指数从0逐项递增到n,是升幂排列
a的指数从n逐项递减到0,是降幂排列
各项的次数都等于n,是关于a与b的齐次多项式
三、新课讲授
四、典型例题
例1、请写出 的展开式。
解:
四、典型例题
例2、求 的二项式展开式中的第6项。
解:
变式1、求 的二项式展开式中的
第6项的二项式系数。
解:
变式2、求 的二项式展开式中
的第6项的系数。
解:
四、典型例题
变式3、求 的二项式展开式中
的倒数第6项。
解:
例2、求 的二项式展开式中的第6项。
四、典型例题
例3、求 二项展开式中的常数项。
解:
五、拓展思考
*求证:
证明:
六、课堂小结
知识方面:二项式定理;
通项;
二项式系数;
思想方法:从特殊到一般;
七、学习情况反馈
自测1:求 的展开式。
自测2:求 的二项展开式中 项的系数。
自测3:求 的二项展开式中的常数项。
自测4:求证:
