人教版六年级下册数学6.3.1统计授课课件(23张PPT)
文档属性
| 名称 | 人教版六年级下册数学6.3.1统计授课课件(23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 19:33:58 | ||
图片预览





文档简介
统 计
<
=
>
+
×
-
÷
1
2
3
人教版小学数学六年级下册
激趣导入
我们学过哪些统计的知识?
那它们都有什么特点?适合在什么情况下使用?现在就来一起学习。
统计图
统计量
统计
统计表
新知讲解
把收集到的数据经过分类、整理后,填在一定格式的表格内,用来反映情况,说明问题,这种表格叫做统计表。
统计表
只含有一个统计项目的统计表。
含有两个或两个以上统计项目的统计表。
统计表
新知讲解
一
二
三
四
五
六
六(1)班
61
94
183
137
129
50
星期
个数
班级
六(1)班同学(周一~周六)第一学期捡废品情况统计表
一
二
三
四
五
六
六(2)班
28
93
54
63
65
96
周数
个数
班级
六(2)班同学(周一~周六)第一学期捡废品情况统计表
单式统计表
新知讲解
一
二
三
四
五
六
六(1)班
61
94
183
137
129
150
六(2)班
28
93
54
63
65
96
星期
个数
班级
六年级同学(周一~周六)第一学期捡废品情况统计表
复式统计表
新知讲解
用点、线、面等相关联的量之间数量的关系的图形,叫做统计图。
统计图
单式条形统计图
复式条形统计图
单式折线统计图
复式折线统计图
统计图
条形统计图
折线统计图
扇形统计图
特点
作用
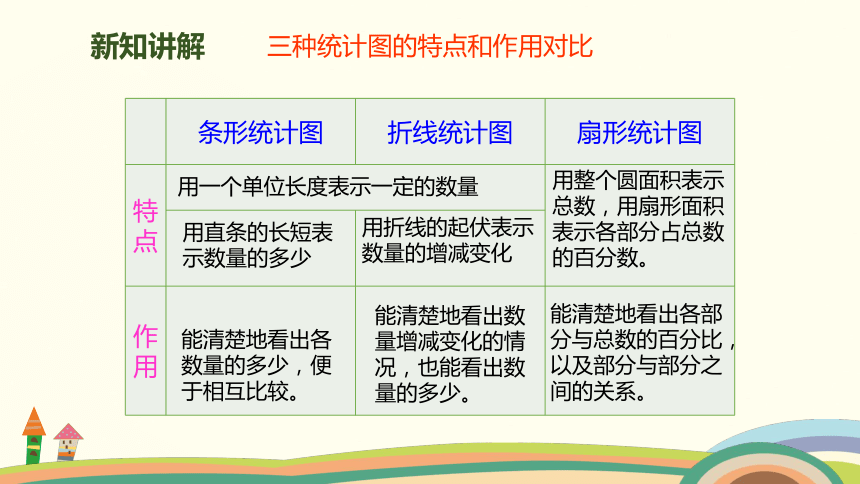
三种统计图的特点和作用对比
用一个单位长度表示一定的数量
用整个圆面积表示总数,用扇形面积表示各部分占总数的百分数。
用直条的长短表示数量的多少
用折线的起伏表示数量的增减变化
能清楚地看出各数量的多少,便于相互比较。
能清楚地看出数量增减变化的情况,也能看出数量的多少。
能清楚地看出各部分与总数的百分比,以及部分与部分之间的关系。
新知讲解
1957年~2050年世界人口变化预测情况。
分别选择合适的统计图表示下列数据,并说明你的理由。
2050年各大洲人口预测达到的具体数据。
2050年世界人口分布预测情况。
1
2
3
新知讲解
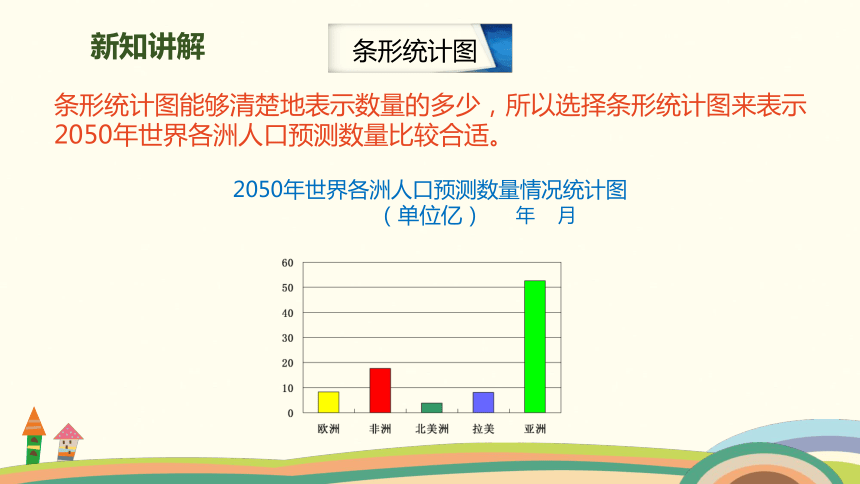
条形统计图能够清楚地表示数量的多少,所以选择条形统计图来表示2050年世界各洲人口预测数量比较合适。
2050年世界各洲人口预测数量情况统计图(单位亿)
年 月
新知讲解
条形统计图
新知讲解
折线统计图不仅能够清楚地表示数量的多少,而且还可以表示数量增减的变化情况,所以选择折线统计图来表示1957年~2050年世界人口变化预测情况比较合适。
1957~2050年世界人口变化预测情况统计图(单位亿)
折线统计图
新知讲解
60.5%
12.5%
12.9%
8%
5.6%
0.5%
扇形统计图能够清楚地表示出部分与总体的关系,所以选择扇形统计图来表2050年世界人口分布预测情况比较合适。
扇形统计图
新知讲解
一组数据的和除以这组数据的个数所得的商叫做这组数据的平均数。一组数据只有一个平均数。
平均数
代表一组数据的平均值
① 移多补少
② 平均数=总数量÷总份数
(总体水平)
中位数
有序排列的一组数据中最中间的那个数据。
(一般水平)
奇数个数据:直接找“最中间”的一个数。
偶数个数据:最中间的那两个数的平均数。
众数
一组数据中出现次数最多的那个数据。一组数据中的众数可以有1个2个以上或没有。
(集中趋势 )
统计量
新知讲解
六(1)班同学身高、体重情况统计表
(1)上面两组数据的平均数各是多少?
新知讲解
(1)上面两组数据的平均数各是多少?
身高平均数:
(1.4+1.43×3+1.46×5+1.49×10+1.52×12+1.55×6+1.58×3)÷40
=60.17÷40≈1.50(m)
体重平均数:
(30×2+33×4+36×5+39×12+42×10+45×4+48×3)÷40
=1584÷40=39.6(kg)
答:身高的平均数是1.50m,体重的平均数是39.6kg。
新知讲解
(2)什么数据能代表全班同学的身高和体重?
众数:
只要看出现次数最多的那个数据。
1.52米出现最多,共12次,所以众数是1.52米。
众数:
众数是39千克,因为人数最多,有12人。
身高/m
1.40
1.43
1.46
1.49
1.52
1.55
1.58
人数
1
3
5
10
12
6
3
(2)小组讨论:什么数据能代表全班同学的身高和体重?
先要把这组数从小到大排列,然后再找中间位置的数。根据表格,这个班一共有40人,从最矮的加到1.49:1+3+5+10=19(人),第20人与第21人都是1.52米,所以中位数应该是1.52 米。
身高中位数:
新知讲解
新知讲解
(2)什么数据能代表全班同学的身高和体重?
答:用平均数表示比较合适。因为它与这组数据中的每个数据都有关系。
平均数:1.50m
中位数:1.52m
众数:1.52m
平均数:39.6kg
中位数:39kg
众数:39kg
下面是四年级两个班1分钟跳绳成绩。
四(1)班1分钟跳绳成绩(个/分) 四(2)班1分钟跳绳成绩(个/分)
80 95 102 120 120 135 98 85 76 105 79 96 85 73
95 82 85 104 84 85 110 105 73 102 120 90 94 85
80 95 102 104 122 76 69 96 85 73 85 104 85 80
76 95 96 89 110 120 85 102 104 65 72 94 73 94
84 85 96 75 124 86 89 122 89 96 84 89 73 105
个数
人数
班级
80及80以下
81~85
86~90
91~95
96~100
100以上
(1)班
(2)班
(1)班的成绩好些。因为跳86个以上的人数,(1)班比(2)班多。
四年级1分钟跳绳成绩表
完成下面的统计表,并说说哪个队的跳绳成绩好些?
6
7
3
4
3
12
10
7
3
3
3
9
练习巩固
看图并回答问题。
短跑 跳高 跳远 铅球 中长跑 项目
25
20
15
10
5
0
成绩(分)
五(1)班和(2)班运动会得分情况统计图
答:五(2)班
答:跳高和跳远
(1)哪个班在短跑项目上占优势?
(2)五(1)班在哪些项目上占优势?
(3)你还有什么发现?
答:在中长跑项目上,(2)班明显占优势;铅球成绩两个班差不多。
看图并回答问题。
我国某两个南北城市2017年月平均最高气温变化情况统计图
(2)1月份两个城市的月平均最高气温相差多少摄氏度?8月份呢?你有什么发现?
(1)说一说这两个城市2017年月平均最高气温变化的趋势。
答:从1月份到7、8月份月平均气温呈上升趋势,从7、8月份到12月份呈下降趋势。
答:1月份两个城市的月平均最高气温相差19℃,8月份相差26℃,我发现冬天温差大,夏天温差小。
为了组织球类比赛,学校调查了六年级学生最喜欢的球类运动情况,统计如下图。
(1)如果喜欢排球运动的有30人,喜欢兵乓球运动的大约有多少人?
30 ÷ 15% = 200(人)
200 × 50% = 100(人)
答:喜欢兵乓球运动的大约有100人。
(2)你认为应该组织哪种球类比赛?为什么?
答:应该组织乒乓球比赛,因为喜欢乒乓球运动的人数最多。若组织比赛,参与度高。
六年级学生最喜欢的球类运动情况统计图
知识总结
统计
把收集到的数据经过分类、整理后,填在一定格式的表格内,用来反映情况,说明问题,这种表格叫做统计表。
点、线、面等相关联的量之间数量的关系的图形,叫做统计图。
谢谢观看
人教版小学数学六年级下册
<
=
>
+
×
-
÷
1
2
3
<
=
>
+
×
-
÷
1
2
3
人教版小学数学六年级下册
激趣导入
我们学过哪些统计的知识?
那它们都有什么特点?适合在什么情况下使用?现在就来一起学习。
统计图
统计量
统计
统计表
新知讲解
把收集到的数据经过分类、整理后,填在一定格式的表格内,用来反映情况,说明问题,这种表格叫做统计表。
统计表
只含有一个统计项目的统计表。
含有两个或两个以上统计项目的统计表。
统计表
新知讲解
一
二
三
四
五
六
六(1)班
61
94
183
137
129
50
星期
个数
班级
六(1)班同学(周一~周六)第一学期捡废品情况统计表
一
二
三
四
五
六
六(2)班
28
93
54
63
65
96
周数
个数
班级
六(2)班同学(周一~周六)第一学期捡废品情况统计表
单式统计表
新知讲解
一
二
三
四
五
六
六(1)班
61
94
183
137
129
150
六(2)班
28
93
54
63
65
96
星期
个数
班级
六年级同学(周一~周六)第一学期捡废品情况统计表
复式统计表
新知讲解
用点、线、面等相关联的量之间数量的关系的图形,叫做统计图。
统计图
单式条形统计图
复式条形统计图
单式折线统计图
复式折线统计图
统计图
条形统计图
折线统计图
扇形统计图
特点
作用
三种统计图的特点和作用对比
用一个单位长度表示一定的数量
用整个圆面积表示总数,用扇形面积表示各部分占总数的百分数。
用直条的长短表示数量的多少
用折线的起伏表示数量的增减变化
能清楚地看出各数量的多少,便于相互比较。
能清楚地看出数量增减变化的情况,也能看出数量的多少。
能清楚地看出各部分与总数的百分比,以及部分与部分之间的关系。
新知讲解
1957年~2050年世界人口变化预测情况。
分别选择合适的统计图表示下列数据,并说明你的理由。
2050年各大洲人口预测达到的具体数据。
2050年世界人口分布预测情况。
1
2
3
新知讲解
条形统计图能够清楚地表示数量的多少,所以选择条形统计图来表示2050年世界各洲人口预测数量比较合适。
2050年世界各洲人口预测数量情况统计图(单位亿)
年 月
新知讲解
条形统计图
新知讲解
折线统计图不仅能够清楚地表示数量的多少,而且还可以表示数量增减的变化情况,所以选择折线统计图来表示1957年~2050年世界人口变化预测情况比较合适。
1957~2050年世界人口变化预测情况统计图(单位亿)
折线统计图
新知讲解
60.5%
12.5%
12.9%
8%
5.6%
0.5%
扇形统计图能够清楚地表示出部分与总体的关系,所以选择扇形统计图来表2050年世界人口分布预测情况比较合适。
扇形统计图
新知讲解
一组数据的和除以这组数据的个数所得的商叫做这组数据的平均数。一组数据只有一个平均数。
平均数
代表一组数据的平均值
① 移多补少
② 平均数=总数量÷总份数
(总体水平)
中位数
有序排列的一组数据中最中间的那个数据。
(一般水平)
奇数个数据:直接找“最中间”的一个数。
偶数个数据:最中间的那两个数的平均数。
众数
一组数据中出现次数最多的那个数据。一组数据中的众数可以有1个2个以上或没有。
(集中趋势 )
统计量
新知讲解
六(1)班同学身高、体重情况统计表
(1)上面两组数据的平均数各是多少?
新知讲解
(1)上面两组数据的平均数各是多少?
身高平均数:
(1.4+1.43×3+1.46×5+1.49×10+1.52×12+1.55×6+1.58×3)÷40
=60.17÷40≈1.50(m)
体重平均数:
(30×2+33×4+36×5+39×12+42×10+45×4+48×3)÷40
=1584÷40=39.6(kg)
答:身高的平均数是1.50m,体重的平均数是39.6kg。
新知讲解
(2)什么数据能代表全班同学的身高和体重?
众数:
只要看出现次数最多的那个数据。
1.52米出现最多,共12次,所以众数是1.52米。
众数:
众数是39千克,因为人数最多,有12人。
身高/m
1.40
1.43
1.46
1.49
1.52
1.55
1.58
人数
1
3
5
10
12
6
3
(2)小组讨论:什么数据能代表全班同学的身高和体重?
先要把这组数从小到大排列,然后再找中间位置的数。根据表格,这个班一共有40人,从最矮的加到1.49:1+3+5+10=19(人),第20人与第21人都是1.52米,所以中位数应该是1.52 米。
身高中位数:
新知讲解
新知讲解
(2)什么数据能代表全班同学的身高和体重?
答:用平均数表示比较合适。因为它与这组数据中的每个数据都有关系。
平均数:1.50m
中位数:1.52m
众数:1.52m
平均数:39.6kg
中位数:39kg
众数:39kg
下面是四年级两个班1分钟跳绳成绩。
四(1)班1分钟跳绳成绩(个/分) 四(2)班1分钟跳绳成绩(个/分)
80 95 102 120 120 135 98 85 76 105 79 96 85 73
95 82 85 104 84 85 110 105 73 102 120 90 94 85
80 95 102 104 122 76 69 96 85 73 85 104 85 80
76 95 96 89 110 120 85 102 104 65 72 94 73 94
84 85 96 75 124 86 89 122 89 96 84 89 73 105
个数
人数
班级
80及80以下
81~85
86~90
91~95
96~100
100以上
(1)班
(2)班
(1)班的成绩好些。因为跳86个以上的人数,(1)班比(2)班多。
四年级1分钟跳绳成绩表
完成下面的统计表,并说说哪个队的跳绳成绩好些?
6
7
3
4
3
12
10
7
3
3
3
9
练习巩固
看图并回答问题。
短跑 跳高 跳远 铅球 中长跑 项目
25
20
15
10
5
0
成绩(分)
五(1)班和(2)班运动会得分情况统计图
答:五(2)班
答:跳高和跳远
(1)哪个班在短跑项目上占优势?
(2)五(1)班在哪些项目上占优势?
(3)你还有什么发现?
答:在中长跑项目上,(2)班明显占优势;铅球成绩两个班差不多。
看图并回答问题。
我国某两个南北城市2017年月平均最高气温变化情况统计图
(2)1月份两个城市的月平均最高气温相差多少摄氏度?8月份呢?你有什么发现?
(1)说一说这两个城市2017年月平均最高气温变化的趋势。
答:从1月份到7、8月份月平均气温呈上升趋势,从7、8月份到12月份呈下降趋势。
答:1月份两个城市的月平均最高气温相差19℃,8月份相差26℃,我发现冬天温差大,夏天温差小。
为了组织球类比赛,学校调查了六年级学生最喜欢的球类运动情况,统计如下图。
(1)如果喜欢排球运动的有30人,喜欢兵乓球运动的大约有多少人?
30 ÷ 15% = 200(人)
200 × 50% = 100(人)
答:喜欢兵乓球运动的大约有100人。
(2)你认为应该组织哪种球类比赛?为什么?
答:应该组织乒乓球比赛,因为喜欢乒乓球运动的人数最多。若组织比赛,参与度高。
六年级学生最喜欢的球类运动情况统计图
知识总结
统计
把收集到的数据经过分类、整理后,填在一定格式的表格内,用来反映情况,说明问题,这种表格叫做统计表。
点、线、面等相关联的量之间数量的关系的图形,叫做统计图。
谢谢观看
人教版小学数学六年级下册
<
=
>
+
×
-
÷
1
2
3
