上海市华二附中2020-2021学年高一上学期12月月考数学试题 Word版含答案
文档属性
| 名称 | 上海市华二附中2020-2021学年高一上学期12月月考数学试题 Word版含答案 |

|
|
| 格式 | doc | ||
| 文件大小 | 491.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 00:00:00 | ||
图片预览

文档简介
华二附中高一12月月考数学试卷
2020.12
一. 填空题
1. 幂函数的图像一定不经过第 象限
2.“”是“为奇函数”的 条件
3. 若集合,集合,则
4. 不等式的解集为
5. 函数的最小值为
6. 若函数的对称中心是,则
7. 若是偶函数,且当时,,则不等式的解集是
8. 若集合是的子集,则的取值范围
是
9. 一系列函数若它们的解析式相同、值域相同,但其定义域不同,则称这一系列函数为“同族函数”,若解析式为,值域为的“同族函数”共有 个
10. 三位同学对问题“关于的不等式在上恒成立,求实数
的取值范围”提出各自的解题思路:
甲说:“这题简单,只须不等式左边的最小值不小于右边的最大值”;
乙说:“不要瞎搞,应该把不等式变形为左边含变量的函数,右边仅含常数,求函数最值”
丙说:“你们二人不讲题德,应该把不等式两边看成关于的函数,作出函数图像才能解决”;
参考上述解题思路,你认为他们所讨论的问题的正确结论,即的取值范围是
11. 已知函数,若函数有三个不同零点,则实
数的取值范围为
12. 已知(,),若,与轴交点为,为
曲线,在上任意一点,总存在一点(异于)使得且,
则
二. 选择题
13. 若关于的不等式的解集是空集,则实数的取值范围是( )
A. B. C. D.
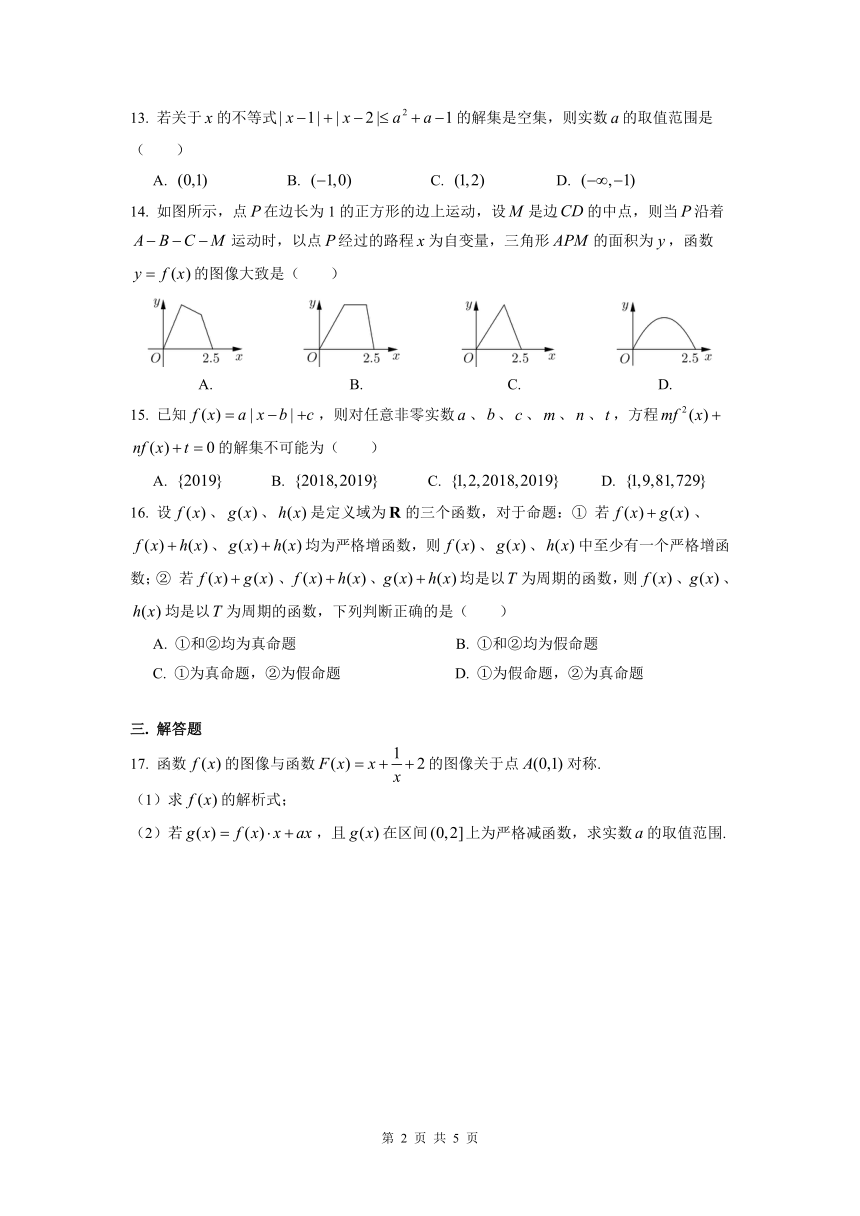
14. 如图所示,点在边长为1的正方形的边上运动,设是边的中点,则当沿着运动时,以点经过的路程为自变量,三角形的面积为,函数的图像大致是( )
A. B. C. D.
15. 已知,则对任意非零实数、、、、、,方程
的解集不可能为( )
A. B. C. D.
16. 设、、是定义域为的三个函数,对于命题:① 若、、均为严格增函数,则、、中至少有一个严格增函数;② 若、、均是以为周期的函数,则、、均是以为周期的函数,下列判断正确的是( )
A. ①和②均为真命题 B. ①和②均为假命题
C. ①为真命题,②为假命题 D. ①为假命题,②为真命题
三. 解答题
17. 函数的图像与函数的图像关于点对称.
(1)求的解析式;
(2)若,且在区间上为严格减函数,求实数的取值范围.
18. 已知函数对任意实数、恒有,且当,,又.
(1)判断的奇偶性,并证明;
(2)求在区间上的最大值;
(3)解关于的不等式.
19. 某游戏厂商对新出品的一款游戏设定了“防沉迷系统”,规则如下:
① 3小时以内(含3小时)为健康时间,玩家在这段时间内获得的累积经验值(单位:)与游戏时间(小时)满足关系式:;
② 3到5小时(含5小时)为疲劳时间,玩家在这段时间内获得的经验值为0(即累积经验值不变);
③ 超过5小时为不健康时间,累计经验值开始损失,损失的经验值与不健康时间成正比列关系,比例系数为50;
(1)当时,写出累积经验值与游玩时间的函数关系式,并求出游玩6小时的累计经验值;
(2)该游戏厂商把累计经验值与游戏时间的比值称为“玩家愉悦指数”,记作;若,且该游戏厂商希望在健康时间内,这款游戏的“玩家愉悦指数”不低于24,求实数的取值范围.
20. 定义凡尔赛函数,已知,,.
(1)求关于的表达式,并求的最小值;
(2)当时,函数在上有唯一零点,求的取值范围;
(3)已知存在,使得对任意的恒成立,求的取值范围.
21. 定义域为的函数,如果对于区间内()的任意三个数、、,当时,都有,则称此函数为区间上的“函数”.
(1)请你写出一个在上的“函数”(不需要证明);
(2)判断幂函数在上是否为“函数”,并证明你的结论;
(3)若函数在区间上是“函数”,求实数的取值范围.
参考答案
一. 填空题
1. 四 2. 非充分非必要 3. 4.
5. 6. 7. 或 8.
9. 9 10. 11. 12.
二. 选择题
13. B 14. A 15. D 16. D
三. 解答题
17.(1);(2).
18.(1)奇函数;(2)6;(3)当时,解集为 ;当时,解集为且
;当时,解集为;当时,解集为或;
当时,解集为或.
19.(1),;(2).
20.(1),的最小值为;
(2);(3).
21.(1);(2)是,证明略;(3).
2020.12
一. 填空题
1. 幂函数的图像一定不经过第 象限
2.“”是“为奇函数”的 条件
3. 若集合,集合,则
4. 不等式的解集为
5. 函数的最小值为
6. 若函数的对称中心是,则
7. 若是偶函数,且当时,,则不等式的解集是
8. 若集合是的子集,则的取值范围
是
9. 一系列函数若它们的解析式相同、值域相同,但其定义域不同,则称这一系列函数为“同族函数”,若解析式为,值域为的“同族函数”共有 个
10. 三位同学对问题“关于的不等式在上恒成立,求实数
的取值范围”提出各自的解题思路:
甲说:“这题简单,只须不等式左边的最小值不小于右边的最大值”;
乙说:“不要瞎搞,应该把不等式变形为左边含变量的函数,右边仅含常数,求函数最值”
丙说:“你们二人不讲题德,应该把不等式两边看成关于的函数,作出函数图像才能解决”;
参考上述解题思路,你认为他们所讨论的问题的正确结论,即的取值范围是
11. 已知函数,若函数有三个不同零点,则实
数的取值范围为
12. 已知(,),若,与轴交点为,为
曲线,在上任意一点,总存在一点(异于)使得且,
则
二. 选择题
13. 若关于的不等式的解集是空集,则实数的取值范围是( )
A. B. C. D.
14. 如图所示,点在边长为1的正方形的边上运动,设是边的中点,则当沿着运动时,以点经过的路程为自变量,三角形的面积为,函数的图像大致是( )
A. B. C. D.
15. 已知,则对任意非零实数、、、、、,方程
的解集不可能为( )
A. B. C. D.
16. 设、、是定义域为的三个函数,对于命题:① 若、、均为严格增函数,则、、中至少有一个严格增函数;② 若、、均是以为周期的函数,则、、均是以为周期的函数,下列判断正确的是( )
A. ①和②均为真命题 B. ①和②均为假命题
C. ①为真命题,②为假命题 D. ①为假命题,②为真命题
三. 解答题
17. 函数的图像与函数的图像关于点对称.
(1)求的解析式;
(2)若,且在区间上为严格减函数,求实数的取值范围.
18. 已知函数对任意实数、恒有,且当,,又.
(1)判断的奇偶性,并证明;
(2)求在区间上的最大值;
(3)解关于的不等式.
19. 某游戏厂商对新出品的一款游戏设定了“防沉迷系统”,规则如下:
① 3小时以内(含3小时)为健康时间,玩家在这段时间内获得的累积经验值(单位:)与游戏时间(小时)满足关系式:;
② 3到5小时(含5小时)为疲劳时间,玩家在这段时间内获得的经验值为0(即累积经验值不变);
③ 超过5小时为不健康时间,累计经验值开始损失,损失的经验值与不健康时间成正比列关系,比例系数为50;
(1)当时,写出累积经验值与游玩时间的函数关系式,并求出游玩6小时的累计经验值;
(2)该游戏厂商把累计经验值与游戏时间的比值称为“玩家愉悦指数”,记作;若,且该游戏厂商希望在健康时间内,这款游戏的“玩家愉悦指数”不低于24,求实数的取值范围.
20. 定义凡尔赛函数,已知,,.
(1)求关于的表达式,并求的最小值;
(2)当时,函数在上有唯一零点,求的取值范围;
(3)已知存在,使得对任意的恒成立,求的取值范围.
21. 定义域为的函数,如果对于区间内()的任意三个数、、,当时,都有,则称此函数为区间上的“函数”.
(1)请你写出一个在上的“函数”(不需要证明);
(2)判断幂函数在上是否为“函数”,并证明你的结论;
(3)若函数在区间上是“函数”,求实数的取值范围.
参考答案
一. 填空题
1. 四 2. 非充分非必要 3. 4.
5. 6. 7. 或 8.
9. 9 10. 11. 12.
二. 选择题
13. B 14. A 15. D 16. D
三. 解答题
17.(1);(2).
18.(1)奇函数;(2)6;(3)当时,解集为 ;当时,解集为且
;当时,解集为;当时,解集为或;
当时,解集为或.
19.(1),;(2).
20.(1),的最小值为;
(2);(3).
21.(1);(2)是,证明略;(3).
同课章节目录
