周周卷(二) 二次函数的图象和性质 习题课件(36张PPT)
文档属性
| 名称 | 周周卷(二) 二次函数的图象和性质 习题课件(36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 19:49:24 | ||
图片预览











文档简介
周周卷(二) 二次函数的图象和性质
测试范围:22.1
选择题
填空题
附加题
解答题
一、选择题(每小题3分,共30分) 1.下列函数属于二次函数的是( )
A.y=-3x2+1 B.y= C.y= D.y=2x+5
A
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
2.抛物线y=-3(x-1)2+6的顶点坐标为( )
A.(1,6) B.(1,-6) C.(-1,-6) D.(-1,6)
A
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
3.将抛物线y=x2先向上平移1个单位长度,再向左平移2个单位长度,则新
抛物线的解析式为( )
A.y=(x-1)2-2 B.y=(x+1)2-2 C.y=(x+2)2+1 D.y=(x-2)2+1
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
4.二次函数y=x2+4x的图象位于( )
A.第一、二、三象限 B.第一、二、四象限
C.第一、三、四象限 D.第二、三、四象限
A
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
5.用一根长60 cm的铁丝围成一个矩形,那么矩形的面积y(cm2)与它的一边
长x(cm)之间的函数关系式为( )
A.y=x2-30x(0<x<30) B.y=-x2+30x(0≤x<30)
C.y=-x2+30x(0<x<30) D.y=-x2+30x(0<x≤30)
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
6.对于二次函数y=2(x+1)(x-3),下列说法正确的是( )
A.图象开口向下
B.当x>1时,y随x的增大而减小
C.图象的对称轴是直线x=-1
D.当x<1时,y随x的增大而减小
D
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
7.如图是某二次函数的图象,则其解析式为( )
A.y=x2-2x+3 B.y=x2-2x-3
C.y=x2+2x+3 D.y=x2+2x-3
B
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
8.抛物线y=ax2+2ax+a2+2的一部分如图所示,那么该抛物线在y轴右侧
与x轴交点的坐标是( ) A.( ,0) B.(1,0)
C.(2,0) D.(3,0)
B
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
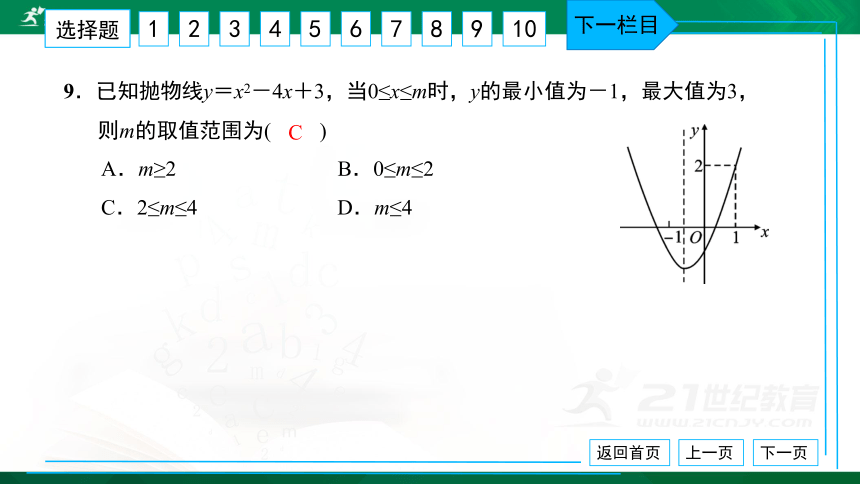
9.已知抛物线y=x2-4x+3,当0≤x≤m时,y的最小值为-1,最大值为3,
则m的取值范围为( ) A.m≥2 B.0≤m≤2
C.2≤m≤4 D.m≤4
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
10.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①a>
0;②a+b+c=2;③bc<0,④a-b+c>0.其中正确的有( ) A.①④ B.①②③ C.①②④ D.②③④
B
解析:∵抛物线开口向上,∴a>0,∴①正确;∵抛物线过点(1,2),∴a+b+c=2,∴②正确;∵对称轴在y轴的左侧,∴a,b同号.∵a>0,∴b>0.∵二次函数的图象与y轴的交点在y轴的负半轴上,∴c<0,∴bc<0,∴③正确;当x=-1时,y=a-b+c<0,∴④不正确.故选B.
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
二、填空题(每小题3分,共24分) 11.如果抛物线y=(a+1)x2-a的开口向下,那么a的取值范围是 .
a<-1
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
12.已知A(-1,y1),B(-2,y2)是抛物线y=-2x2上的两点,则y1 y2.
(填“>”“<”或“=”)
>
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
13.某二次函数图象的顶点坐标是(-1,4),且过点(2,-5),则这个二次函
数的解析式是 .
y=-(x+1)2+4
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
14.若二次函数y=2x2-4x+m有最小值是3,则m= .
5
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
15.若二次函数y=(m+1)x2+m2-2m-3的图象经过原点,则m= .
3
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
16.如图,在同一坐标系中,作出①y=a1x2,②y=a2x2,③y=a3x2的图象,
则a1,a2,a3的大小关系是 .
a1>a2>a3
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
17.已知二次函数y1=x2+2x-3的图象如图所示,将此函数图象向右平移
2个单位长度得抛物线y2的图象,则阴影部分的面积为 .
8
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
18.如图,在平面直角坐标系中,点A在抛物线y=x2-2x+3上运动,过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连接BD,则对角线BD的最小值为 .
解析:∵y=x2-2x+3=(x-1)2+2,∴抛物线的顶点坐标为(1,2),∴当点A在抛物线的顶点时,AC最小,最小值为2.∵四边形ABCD是矩形,∴AC=BD,∴对角线BD的最小值为2.
2
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
三、解答题(共66分) 19.(8分)已知抛物线y=x2-4x+c经过点(0,9). (1)求c的值; (2)若点A(3,y1),B(4,y2)在该抛物线上,试比较y1,y2的大小.
解:(1)当x=0时,y=c=9,∴c的值为9.
(2)由(1)可知抛物线的解析式为y=x2-4x+9. 当x=3时,y1=9-4×3+9=6; 当x=4时,y2=16-4×4+9=9. ∵6<9,∴y1<y2.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
20.(8分)在平面直角坐标系中,二次函数y=ax2+bx+3的图象经过点A(3,0)
和点B(4,3). (1)求二次函数的解析式;
(2)直接画出函数的图象(不列表).
解:(1)∵抛物线y=ax2+bx+3经过点A(3,0)和点B(4,3), ∴ 解得
∴二次函数的解析式为y=x2-4x+3. (2)函数图象如图所示.
9a+3b+3=0,
16a+4b+3=3,
a=1,
b=-4,
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
21.(10分)把二次函数y=a(x-h)2+k的图象先向左平移2个单位长度,再向
上平移4个单位长度,得到二次函数y=-2(1)(x+1)2-1的图象. (1)试确定a,h,k的值;
解:(1)二次函数y=- (x+1)2-1的图象的顶点坐标为(-1,-1),把点(-1,-1)先向右平移2个单位长度,再向下平移4个单位长度得到点的坐标为(1,-5), ∴原二次函数的解析式为y=- (x-1)2-5, ∴a=- ,h=1,k=-5.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)指出二次函数y=a(x-h)2+k图象的开口方向、对称轴和顶点坐标.
解:∵y=a(x-h)2+k=- (x-1)2-5, ∴二次函数的开口向下,对称轴为直线x=1,顶点坐标为(1,-5).
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
22.(8分)如图,在平面直角坐标系中,抛物线y=ax2+3与y轴交于点A,过
点A与x轴平行的直线交抛物线y= x2于点B,C,求BC的长度.
解:当x=0时,y=ax2+3=3, ∴点A的坐标为(0,3). ∵BC∥x轴, ∴点B,C的纵坐标都为3. 在y= x2中,当y=3时, x2=3, 解得x1=3,x2=-3, ∴点B的坐标为(-3,0),点C的坐标为(3,0), ∴BC=3-(-3)=6.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
23.(10分)如图,一小球从地面抛出,运动路线呈抛物线,当小球离抛出地的
水平距离为30 m时,达到最大高度10 m. (1)小球被抛出多远?并求出该抛物线的解析式;
解:(1)根据题意,设抛物线的解析式为y=a(x-30)2+10, 把(0,0)代入,得a=- , ∴抛物线的解析式为y=- (x-30)2+10=- x2+ x. ∵抛物线的对称轴为直线x=30,抛物线与x轴的一个交点坐标为(0,0), ∴抛物线与x轴的另一个交点坐标为(60,0), ∴球被抛出60 m远.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)当小球的高度为 m时,小球离抛出地的水平距离是多少?
解:当y= 时,- (x-30)2+10= ,解得x1=50,x2=10. 答:球离抛出地的水平距离是10 m或50 m.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
24.(10分)设二次函数y1,y2的图象的顶点坐标分别为(a,b),(c,d),当a=
-2c,b=-2d,且开口方向相同时,称y1是y2的“反倍顶二次函数”. (1)请写出二次函数y=x2+x+1的一个“反倍顶二次函数”;
解:(1)∵y=x2+x+1=(x+ )2+ , ∴二次函数y=x2+x+1的图象的顶点坐标为(- , ), ∴二次函数y=x2+x+1的“反倍顶二次函数”的顶点坐标为(1,- ), ∴二次函数y=x2+x+1的一个“的反倍顶二次函数”的解析式为 y=(x-1)2- =x2-2x- .
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)已知关于x的二次函数y1=x2+nx和二次函数y2=x2-2nx+1,若二次函数
y1恰是y1+y2的“反倍顶二次函数”,求n的值.
解:∵y1=x2+nx=(x+ )2+ ,∴其图象的顶点坐标为(- , - ). ∵y1+y2=x2+nx+x2-2nx+1=2x2-nx+1=2(x- )+1- , ∴其图象的顶点坐标为( ,1- ). ∵二次函数y1恰是y1+y2的“反倍顶二次函数”, ∴- =-2×(1- ),解得n=±2.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
25.(12分)如图,已知抛物线y=-x2+2x+m. (1)如果抛物线与x轴交于点A(3,0),C,与y轴交于点B,求抛物线的
解析式及点B,C的坐标;
解:(1)∵抛物线过点A(3,0), ∴-9+6+m=0,解得m=3, ∴抛物线的解析式为y=-x2+2x+3. 令y=0,则-x2+2x+3=0,解得x1=3,x2=-1, ∴点C的坐标为(-1,0).令x=0,得y=3, ∴点B的坐标为(0,3).
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)作直线AB与这条抛物线的对称轴交于点P,求直线AB的解析式和点P的坐标;
解:设直线AB的解析式为y=kx+b,将A(3,0),B(0,3)代入,得
解得 ∴直线AB的解析式为y=-x+3. ∵抛物线y=-x2+2x+3=-(x-1)2+4, ∴对称轴为直线x=1.把x=1代入y=-x+3,得y=2, ∴点P的坐标为(1,2).
k=-1,
b=3,
3k+b=0,
b=3.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(3)该抛物线上有一点D(x,y),使得S△ABC=S△ACD,求点D的坐标.
解:根据题意,得点D的纵坐标为±3. 把y=3代入y=-x2+2x+3,得-x2+2x+3=3,解得x=0或2; 把y=-3代入y=-x2+2x+3,得-x2+2x+3=-3,解得x=1± , ∴点D的坐标为(2,3)或(1- ,-3)或(1+ ,-3).
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
附加题(20分) 已知二次函数y=x2-2mx+m2-1. (1)当二次函数的图象经过坐标原点O(0,0)时,求二次函数的解析式;
解:(1)将点O(0,0)代入二次函数 y=x2-2mx+m2-1中, 得m2-1=0,解得m=±1, ∴二次函数的解析式为y=x2-2x或y=x2+2x.
上一栏目
附加题
(2)如图,当m=2时,该抛物线与y轴交于点C,顶点为D,求C,D两点的坐标;
解:当m=2时, 二次函数解析式为y=x2-4x+3=(x-2)2-1, ∴点C的坐标为(0,3),点D的坐标为(2,-1).
上一栏目
附加题
(3)在(2)的条件下,x轴上是否存在一点P,使得PC+PD最短?若存在,求出
点P的坐标;若不存在,请说明理由.
解:存在. 连接CD.根据“两点之间,线段最短”可知,当点P位于CD
与x轴的交点时,PC+PD最短. 设经过C,D两点的直线解析式为y=kx+b,将C(0,3),D(2,-1)两点坐标代入,得 解得 ∴y=-2x+3.令y=0,得-2x+3=0,解得x= , ∴当点P的坐标为( ,0)时,PC+PD最短.
b=3,
2k+b=-1,
k=-2,
b=3,
上一栏目
附加题
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
测试范围:22.1
选择题
填空题
附加题
解答题
一、选择题(每小题3分,共30分) 1.下列函数属于二次函数的是( )
A.y=-3x2+1 B.y= C.y= D.y=2x+5
A
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
2.抛物线y=-3(x-1)2+6的顶点坐标为( )
A.(1,6) B.(1,-6) C.(-1,-6) D.(-1,6)
A
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
3.将抛物线y=x2先向上平移1个单位长度,再向左平移2个单位长度,则新
抛物线的解析式为( )
A.y=(x-1)2-2 B.y=(x+1)2-2 C.y=(x+2)2+1 D.y=(x-2)2+1
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
4.二次函数y=x2+4x的图象位于( )
A.第一、二、三象限 B.第一、二、四象限
C.第一、三、四象限 D.第二、三、四象限
A
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
5.用一根长60 cm的铁丝围成一个矩形,那么矩形的面积y(cm2)与它的一边
长x(cm)之间的函数关系式为( )
A.y=x2-30x(0<x<30) B.y=-x2+30x(0≤x<30)
C.y=-x2+30x(0<x<30) D.y=-x2+30x(0<x≤30)
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
6.对于二次函数y=2(x+1)(x-3),下列说法正确的是( )
A.图象开口向下
B.当x>1时,y随x的增大而减小
C.图象的对称轴是直线x=-1
D.当x<1时,y随x的增大而减小
D
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
7.如图是某二次函数的图象,则其解析式为( )
A.y=x2-2x+3 B.y=x2-2x-3
C.y=x2+2x+3 D.y=x2+2x-3
B
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
8.抛物线y=ax2+2ax+a2+2的一部分如图所示,那么该抛物线在y轴右侧
与x轴交点的坐标是( ) A.( ,0) B.(1,0)
C.(2,0) D.(3,0)
B
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
9.已知抛物线y=x2-4x+3,当0≤x≤m时,y的最小值为-1,最大值为3,
则m的取值范围为( ) A.m≥2 B.0≤m≤2
C.2≤m≤4 D.m≤4
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
10.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①a>
0;②a+b+c=2;③bc<0,④a-b+c>0.其中正确的有( ) A.①④ B.①②③ C.①②④ D.②③④
B
解析:∵抛物线开口向上,∴a>0,∴①正确;∵抛物线过点(1,2),∴a+b+c=2,∴②正确;∵对称轴在y轴的左侧,∴a,b同号.∵a>0,∴b>0.∵二次函数的图象与y轴的交点在y轴的负半轴上,∴c<0,∴bc<0,∴③正确;当x=-1时,y=a-b+c<0,∴④不正确.故选B.
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
二、填空题(每小题3分,共24分) 11.如果抛物线y=(a+1)x2-a的开口向下,那么a的取值范围是 .
a<-1
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
12.已知A(-1,y1),B(-2,y2)是抛物线y=-2x2上的两点,则y1 y2.
(填“>”“<”或“=”)
>
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
13.某二次函数图象的顶点坐标是(-1,4),且过点(2,-5),则这个二次函
数的解析式是 .
y=-(x+1)2+4
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
14.若二次函数y=2x2-4x+m有最小值是3,则m= .
5
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
15.若二次函数y=(m+1)x2+m2-2m-3的图象经过原点,则m= .
3
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
16.如图,在同一坐标系中,作出①y=a1x2,②y=a2x2,③y=a3x2的图象,
则a1,a2,a3的大小关系是 .
a1>a2>a3
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
17.已知二次函数y1=x2+2x-3的图象如图所示,将此函数图象向右平移
2个单位长度得抛物线y2的图象,则阴影部分的面积为 .
8
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
18.如图,在平面直角坐标系中,点A在抛物线y=x2-2x+3上运动,过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连接BD,则对角线BD的最小值为 .
解析:∵y=x2-2x+3=(x-1)2+2,∴抛物线的顶点坐标为(1,2),∴当点A在抛物线的顶点时,AC最小,最小值为2.∵四边形ABCD是矩形,∴AC=BD,∴对角线BD的最小值为2.
2
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
三、解答题(共66分) 19.(8分)已知抛物线y=x2-4x+c经过点(0,9). (1)求c的值; (2)若点A(3,y1),B(4,y2)在该抛物线上,试比较y1,y2的大小.
解:(1)当x=0时,y=c=9,∴c的值为9.
(2)由(1)可知抛物线的解析式为y=x2-4x+9. 当x=3时,y1=9-4×3+9=6; 当x=4时,y2=16-4×4+9=9. ∵6<9,∴y1<y2.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
20.(8分)在平面直角坐标系中,二次函数y=ax2+bx+3的图象经过点A(3,0)
和点B(4,3). (1)求二次函数的解析式;
(2)直接画出函数的图象(不列表).
解:(1)∵抛物线y=ax2+bx+3经过点A(3,0)和点B(4,3), ∴ 解得
∴二次函数的解析式为y=x2-4x+3. (2)函数图象如图所示.
9a+3b+3=0,
16a+4b+3=3,
a=1,
b=-4,
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
21.(10分)把二次函数y=a(x-h)2+k的图象先向左平移2个单位长度,再向
上平移4个单位长度,得到二次函数y=-2(1)(x+1)2-1的图象. (1)试确定a,h,k的值;
解:(1)二次函数y=- (x+1)2-1的图象的顶点坐标为(-1,-1),把点(-1,-1)先向右平移2个单位长度,再向下平移4个单位长度得到点的坐标为(1,-5), ∴原二次函数的解析式为y=- (x-1)2-5, ∴a=- ,h=1,k=-5.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)指出二次函数y=a(x-h)2+k图象的开口方向、对称轴和顶点坐标.
解:∵y=a(x-h)2+k=- (x-1)2-5, ∴二次函数的开口向下,对称轴为直线x=1,顶点坐标为(1,-5).
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
22.(8分)如图,在平面直角坐标系中,抛物线y=ax2+3与y轴交于点A,过
点A与x轴平行的直线交抛物线y= x2于点B,C,求BC的长度.
解:当x=0时,y=ax2+3=3, ∴点A的坐标为(0,3). ∵BC∥x轴, ∴点B,C的纵坐标都为3. 在y= x2中,当y=3时, x2=3, 解得x1=3,x2=-3, ∴点B的坐标为(-3,0),点C的坐标为(3,0), ∴BC=3-(-3)=6.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
23.(10分)如图,一小球从地面抛出,运动路线呈抛物线,当小球离抛出地的
水平距离为30 m时,达到最大高度10 m. (1)小球被抛出多远?并求出该抛物线的解析式;
解:(1)根据题意,设抛物线的解析式为y=a(x-30)2+10, 把(0,0)代入,得a=- , ∴抛物线的解析式为y=- (x-30)2+10=- x2+ x. ∵抛物线的对称轴为直线x=30,抛物线与x轴的一个交点坐标为(0,0), ∴抛物线与x轴的另一个交点坐标为(60,0), ∴球被抛出60 m远.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)当小球的高度为 m时,小球离抛出地的水平距离是多少?
解:当y= 时,- (x-30)2+10= ,解得x1=50,x2=10. 答:球离抛出地的水平距离是10 m或50 m.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
24.(10分)设二次函数y1,y2的图象的顶点坐标分别为(a,b),(c,d),当a=
-2c,b=-2d,且开口方向相同时,称y1是y2的“反倍顶二次函数”. (1)请写出二次函数y=x2+x+1的一个“反倍顶二次函数”;
解:(1)∵y=x2+x+1=(x+ )2+ , ∴二次函数y=x2+x+1的图象的顶点坐标为(- , ), ∴二次函数y=x2+x+1的“反倍顶二次函数”的顶点坐标为(1,- ), ∴二次函数y=x2+x+1的一个“的反倍顶二次函数”的解析式为 y=(x-1)2- =x2-2x- .
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)已知关于x的二次函数y1=x2+nx和二次函数y2=x2-2nx+1,若二次函数
y1恰是y1+y2的“反倍顶二次函数”,求n的值.
解:∵y1=x2+nx=(x+ )2+ ,∴其图象的顶点坐标为(- , - ). ∵y1+y2=x2+nx+x2-2nx+1=2x2-nx+1=2(x- )+1- , ∴其图象的顶点坐标为( ,1- ). ∵二次函数y1恰是y1+y2的“反倍顶二次函数”, ∴- =-2×(1- ),解得n=±2.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
25.(12分)如图,已知抛物线y=-x2+2x+m. (1)如果抛物线与x轴交于点A(3,0),C,与y轴交于点B,求抛物线的
解析式及点B,C的坐标;
解:(1)∵抛物线过点A(3,0), ∴-9+6+m=0,解得m=3, ∴抛物线的解析式为y=-x2+2x+3. 令y=0,则-x2+2x+3=0,解得x1=3,x2=-1, ∴点C的坐标为(-1,0).令x=0,得y=3, ∴点B的坐标为(0,3).
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)作直线AB与这条抛物线的对称轴交于点P,求直线AB的解析式和点P的坐标;
解:设直线AB的解析式为y=kx+b,将A(3,0),B(0,3)代入,得
解得 ∴直线AB的解析式为y=-x+3. ∵抛物线y=-x2+2x+3=-(x-1)2+4, ∴对称轴为直线x=1.把x=1代入y=-x+3,得y=2, ∴点P的坐标为(1,2).
k=-1,
b=3,
3k+b=0,
b=3.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(3)该抛物线上有一点D(x,y),使得S△ABC=S△ACD,求点D的坐标.
解:根据题意,得点D的纵坐标为±3. 把y=3代入y=-x2+2x+3,得-x2+2x+3=3,解得x=0或2; 把y=-3代入y=-x2+2x+3,得-x2+2x+3=-3,解得x=1± , ∴点D的坐标为(2,3)或(1- ,-3)或(1+ ,-3).
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
附加题(20分) 已知二次函数y=x2-2mx+m2-1. (1)当二次函数的图象经过坐标原点O(0,0)时,求二次函数的解析式;
解:(1)将点O(0,0)代入二次函数 y=x2-2mx+m2-1中, 得m2-1=0,解得m=±1, ∴二次函数的解析式为y=x2-2x或y=x2+2x.
上一栏目
附加题
(2)如图,当m=2时,该抛物线与y轴交于点C,顶点为D,求C,D两点的坐标;
解:当m=2时, 二次函数解析式为y=x2-4x+3=(x-2)2-1, ∴点C的坐标为(0,3),点D的坐标为(2,-1).
上一栏目
附加题
(3)在(2)的条件下,x轴上是否存在一点P,使得PC+PD最短?若存在,求出
点P的坐标;若不存在,请说明理由.
解:存在. 连接CD.根据“两点之间,线段最短”可知,当点P位于CD
与x轴的交点时,PC+PD最短. 设经过C,D两点的直线解析式为y=kx+b,将C(0,3),D(2,-1)两点坐标代入,得 解得 ∴y=-2x+3.令y=0,得-2x+3=0,解得x= , ∴当点P的坐标为( ,0)时,PC+PD最短.
b=3,
2k+b=-1,
k=-2,
b=3,
上一栏目
附加题
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
