周周卷(六) 图形的相似与相似三角形的判定 习题课件(36张PPT)
文档属性
| 名称 | 周周卷(六) 图形的相似与相似三角形的判定 习题课件(36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 19:56:08 | ||
图片预览









文档简介
周周卷(六) 图形的相似与相
似三角形的判定
测试范围:24.2~24.4
选择题
填空题
附加题
解答题
一、选择题(每小题3分,共30分) 1.一把矩形米尺的长为1 m,宽为3 cm,则这把米尺的长与宽的比为( ) A.100∶3 B.1∶3 C.10∶3 D.1000∶3
A
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
2.如图,已知AB∥CD∥EF,AC=4,CE=1,BD=3,则DF的长为( ) A. B. C. D.1
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
3.已知 = ,那么 的值为( ) A.7 B.-7 C. D.-
D
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
4.如图,下列条件中,不能判定△ACD∽△ABC的是( ) A.∠ADC=∠ACB B.∠B=∠ACD
C.∠ACD=∠BCD D. =
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
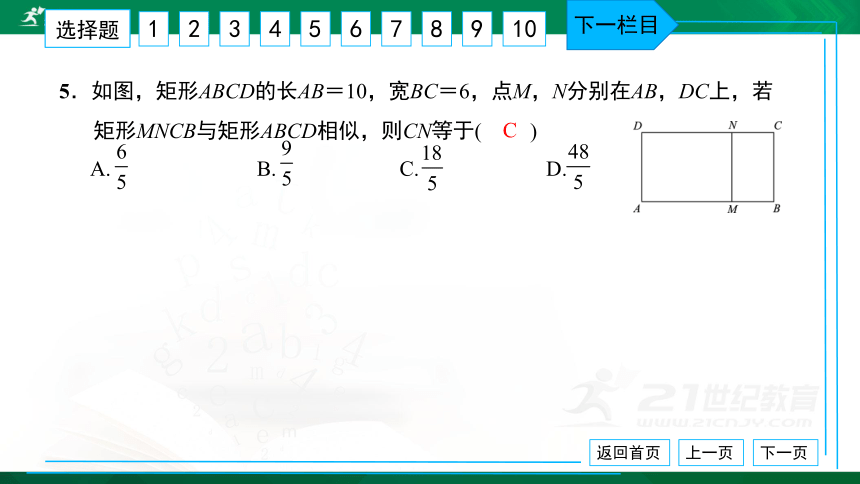
5.如图,矩形ABCD的长AB=10,宽BC=6,点M,N分别在AB,DC上,若
矩形MNCB与矩形ABCD相似,则CN等于( ) A. B. C. D.
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
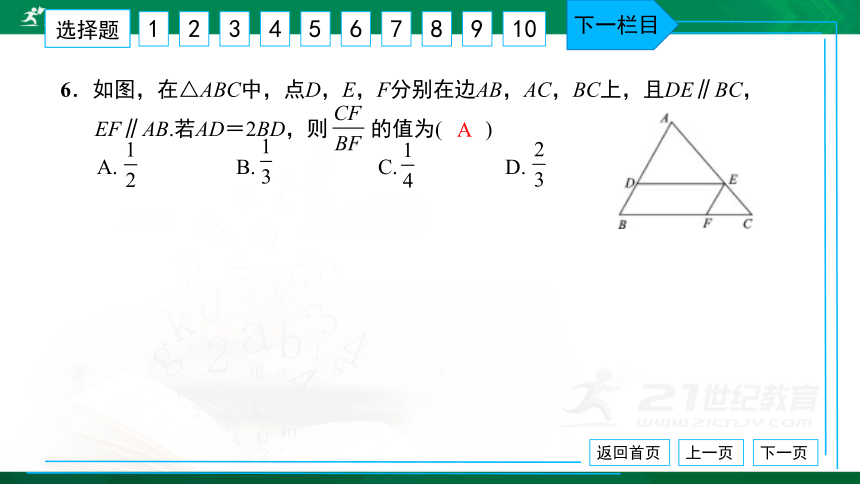
6.如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,且DE∥BC,
EF∥AB.若AD=2BD,则 的值为( ) A. B. C. D.
A
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
7.下列四个三角形中,与如图所示的三角形相似的是( ) A. B. C. D.
B
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
8.“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,
问井深几何?”这是我国古代数学著作《九章算术》中的“井深几何”问题,
它的题意可以由图获得,则井深为( ) A.1.25尺 B.57.5尺 C.6.25尺 D.56.5尺
B
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
9.如图,BE,CF为△ABC的两条高,若AB=6,BC=5,EF=3,则AE的长
为( ) A. B.4 C. D.
A
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
10.如图,AD∥BC,∠D=90°,DC=7,AD=2,BC=4.若在边DC上有点
P使△PAD和△PBC相似,则这样的点P有( ) A.1个 B.2个 C.3个 D.4个
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
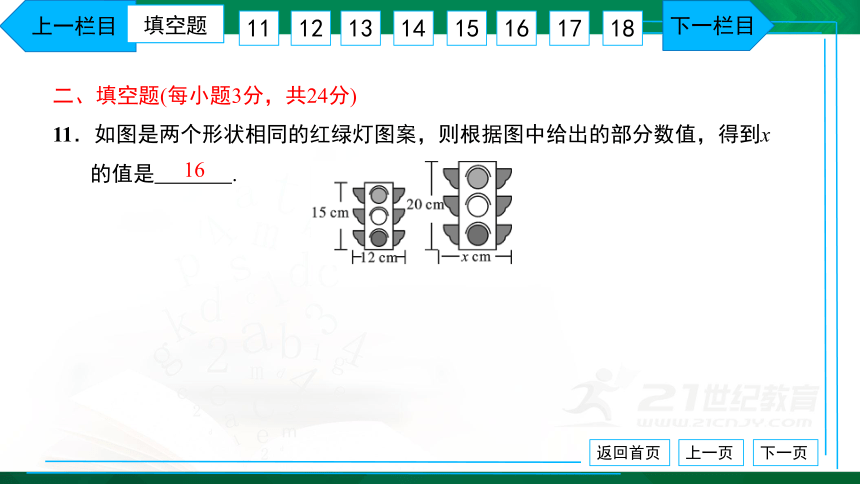
二、填空题(每小题3分,共24分) 11.如图是两个形状相同的红绿灯图案,则根据图中给出的部分数值,得到x
的值是 .
16
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
12.如图,在△ABC中,点M,N分别在边AB,AC上,且MN∥BC.若AM=2,
BM=5,MN=2,则BC= .
7
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
13.如图,在△ADE和△ABC中,∠1=∠2,请添加一个适当的条件∠D=
,使△ADE∽△ABC.(只填一个即可)
∠B或∠E=∠C或
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
14.如图,在△ABC中,∠C=90°,D是AC上一点,DE⊥AB于点E,若AC
=8,BC=6,DE=3,则AD的长为 .
5
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
15.若 = = ,且a+b-c=1,则b+c-a的值为 .
5
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
16.如图,一束光线从y轴上点A(0,1)处发出,经过x轴上点C反射后,经过点
B(6,2),则点C的坐标是 .
(2,0)
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
17.如图,在边长为9的正三角形ABC中,BD=3,∠ADE=60°,则AE的长为
.
7
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
18.如图,在平行四边形ABCD中,E为AB的中点,F为AD上一点,EF交AC
于点G,AF=2 cm,DF=4 cm,AG=3 cm,则AC的长为 .
15 cm
解析:延长FE,CB交于点H.∵四边形ABCD是平行四边形,∴BC=AD=6 cm,BC∥AD,∴∠EAF=∠EBH,∠AFE=∠BHE.∵AE=BE,∴△AFE △BHE,∴BH=AF=2 cm,∴CH=BC+BH=8 cm.∵BC∥AD,∴ = ,即 = ,解得CG=12,则AC=AG+CG=15 cm.
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
三、解答题(共66分) 19.(8分)已知线段a=3,b=8,c=6,d=4. (1)线段a,b,c,d是否成比例? (2)线段a,d,c,b是否成比例?
解:(1)∵3∶8≠6∶4, ∴线段a,b,c,d不成比例.
(2)∵3∶4=6∶8, ∴线段a,d,c,b成比例.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
20.(8分)如图,已知a∥b∥c,n,m分别与a,b,c交于点B,D,F和点A,C,E. (1)若AC=6 cm,CE=4 cm,BD=8 cm,求线段DF的长; (2)若AE∶CE=5∶2,BD=5 cm,求线段DF的长.
解:(1)∵a∥b∥c,∴ = , 即 = ,解得DF= .
(2)∵AE∶CE=5∶2,∴AC∶CE=3∶2. ∵a∥b∥c,∴ = = , 即 = ,解得DF= .
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
21.(8分)如图,在△ABC中,AD是中线,且CD2=BE?BA.求证:ED?AB=AD?BD.
证明:∵AD是中线, ∴BD=CD. ∵CD2=BE?BA, ∴BD2=BE?BA,即 = . 又∵∠B=∠B, ∴△BDE∽△BAD, ∴ = , ∴ED?AB=AD?BD.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
22.(10分)如图,在正方形ABCD中,点M,N分别在AB,BC上,AB=4,AM=1,
BN= . (1)求证:△ADM∽△BMN;
证明:∵四边形ABCD是正方形, ∴AD=AB=4,∠A=∠B=90°. ∵AM=1,∴BM=3, ∴ = = , = ,∴ = . 又∵∠A=∠B=90°, ∴△ADM∽△BMN.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
解:∵△ADM∽△BMN, ∴∠ADM=∠BMN. ∵∠ADM+∠AMD=90°, ∴∠AMD+∠BMN=90°, ∴∠DMN=180°-90°=90°.
(2)求∠DMN的度数.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
23.(10分)如图,在△ABC中,D是BC的中点,且AD=AC,DE⊥BC交AB于
点E,EC交AD于点F. (1)求证:△ABC∽△FCD;
证明:∵D是BC的中点,∴BD=CD. ∵DE⊥BC,∴∠BDE=∠CDE=90°. 又∵DE=DE,∴△BDE △CDE, ∴∠B=∠ECB. ∵AD=AC,∴∠ADC=∠ACB, ∴△ABC∽△FCD.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)求 的值.
解:∵△ABC∽△FCD, ∴ = . ∵D是BC的中点,∴BC=2CD,∴AD=AC=2FD. ∵∠ACD=∠ADC=∠B+∠EAD,∠B=∠FCD, ∴∠EAD=∠ACE,∴△EAF∽△ECA, ∴ = = = , ∴EC=2EA=4EF, ∴ =3.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
24.(10分)如图,P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD
于点E,交BA的延长线于点F. (1)求证:△APE∽△FPA;
证明:∵四边形ABCD是菱形, ∴AD=CD,∠ADP=∠CDP. 在△APD和△CPD中, ∴△APD △CPD(SAS),∴∠DAP=∠DCP. ∵CD∥BF,∴∠DCP=∠F,∴∠DAP=∠F. 又∵∠APE=∠FPA,∴△APE∽△FPA.
AD=CD,
∠ADP=∠CDP,
PD=PD,
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)若PE=2,EF=6,求PC的长.
解:∵△APE∽△FPA,∴ = ,∴PA2=PE?PF. ∵△APD △CPD,∴PA=PC,∴PC2=PE?PF. ∵PE=2,EF=6,∴PF=PE+EF=2+6=8,∴PC2=2×8=16, ∴PC=4.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
25.(12分)(1)问题:如图1,在四边形ABCD中,P为AB上一点,∠DPC=∠A
=∠B=90°,求证:AD?BC=AP?BP;
证明:∵∠DPC=∠A=∠B=90°, ∴∠ADP+∠APD=90°,∠BPC+∠APD=90°, ∴∠ADP=∠BPC,∴△ADP∽△BPC,
∴ = ,∴AD?BC=AP?BP.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)探究:如图2,在四边形ABCD中,P为AB上一点,当∠DPC=∠A=∠B=θ
时,上述结论是否依然成立?请说明理由;
解:结论AD?BC=AP?BP仍然成立.理由: ∵∠BPD=∠DPC+∠BPC,∠BPD=∠A+∠ADP, ∴∠DPC+∠BPC=∠A+∠ADP. ∵∠DPC=∠A=∠B=θ,∴∠BPC=∠ADP,∴△ADP∽△BPC, ∴ = ,∴AD?BC=AP?BP.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(3)应用:请利用(1)(2)获得的经验解决问题: 如图3,在△ABD中,AB=6,AD=BD=5,点P以每秒1个单位
长度的速度,由点A出发,沿边AB向点B运动,且满足∠CPD=
∠A.设点P的运动时间为t(秒),当DC=4BC时,求t的值.
解:∵DC=4BC, AD=BD=5,∴DC=4,BC=1. 由(1)(2)可知AD?BC=AP?BP, ∴5×1=t(6-t),解得t1=1,t2=5, ∴t的值为1或5.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
附加题(20分) 阅读材料,如图1, O中的任意两条弦AC,BD交于点P,若连接AB,CD,易证△ABP∽△DCP,则PA∶PD=PB∶PC,即PA·PC=PB·PD. 解决下列问题: (1)若PA=3PC=6,且P为BD中点,则BD= ;
上一栏目
附加题
(2)如图2,直线AB,CD交于点Q. ①求证:QA·QB=QC·QD;
①证明:∵四边形ABDC为圆内接四边形, ∴∠QAC=∠D. ∵∠Q=∠Q,∠QAC=∠D, ∴△QAC∽△QDB, ∴QA∶QD=QC∶QB, 即QA·QB=QC·QD.
上一栏目
附加题
②由①的结论可以猜想:当点A,B重合,即QA与 O相切于点A时,QA2=
QC·QD,作图并说明此猜想是否正确.
②解:作图略. QA与 O相切于点A,连接AO,并延长交 O于点N,连接CN. ∵QA与 O相切,∴AN⊥AQ,∴∠NAC+∠CAQ=90°. ∵AN为直径,∴∠ACN=90°,∴∠NAC+∠N=90°,∴∠CAQ=∠N. ∵ = ,∴∠N=∠D,∴∠CAQ=∠D.
∵∠Q=∠Q,∠CAQ=∠D,∴△QAC∽△QDA,∴QA∶QD=QC∶QA,
即QA2=QC·QD,∴此猜想正确.
上一栏目
附加题
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
似三角形的判定
测试范围:24.2~24.4
选择题
填空题
附加题
解答题
一、选择题(每小题3分,共30分) 1.一把矩形米尺的长为1 m,宽为3 cm,则这把米尺的长与宽的比为( ) A.100∶3 B.1∶3 C.10∶3 D.1000∶3
A
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
2.如图,已知AB∥CD∥EF,AC=4,CE=1,BD=3,则DF的长为( ) A. B. C. D.1
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
3.已知 = ,那么 的值为( ) A.7 B.-7 C. D.-
D
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
4.如图,下列条件中,不能判定△ACD∽△ABC的是( ) A.∠ADC=∠ACB B.∠B=∠ACD
C.∠ACD=∠BCD D. =
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
5.如图,矩形ABCD的长AB=10,宽BC=6,点M,N分别在AB,DC上,若
矩形MNCB与矩形ABCD相似,则CN等于( ) A. B. C. D.
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
6.如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,且DE∥BC,
EF∥AB.若AD=2BD,则 的值为( ) A. B. C. D.
A
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
7.下列四个三角形中,与如图所示的三角形相似的是( ) A. B. C. D.
B
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
8.“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,
问井深几何?”这是我国古代数学著作《九章算术》中的“井深几何”问题,
它的题意可以由图获得,则井深为( ) A.1.25尺 B.57.5尺 C.6.25尺 D.56.5尺
B
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
9.如图,BE,CF为△ABC的两条高,若AB=6,BC=5,EF=3,则AE的长
为( ) A. B.4 C. D.
A
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
10.如图,AD∥BC,∠D=90°,DC=7,AD=2,BC=4.若在边DC上有点
P使△PAD和△PBC相似,则这样的点P有( ) A.1个 B.2个 C.3个 D.4个
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
二、填空题(每小题3分,共24分) 11.如图是两个形状相同的红绿灯图案,则根据图中给出的部分数值,得到x
的值是 .
16
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
12.如图,在△ABC中,点M,N分别在边AB,AC上,且MN∥BC.若AM=2,
BM=5,MN=2,则BC= .
7
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
13.如图,在△ADE和△ABC中,∠1=∠2,请添加一个适当的条件∠D=
,使△ADE∽△ABC.(只填一个即可)
∠B或∠E=∠C或
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
14.如图,在△ABC中,∠C=90°,D是AC上一点,DE⊥AB于点E,若AC
=8,BC=6,DE=3,则AD的长为 .
5
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
15.若 = = ,且a+b-c=1,则b+c-a的值为 .
5
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
16.如图,一束光线从y轴上点A(0,1)处发出,经过x轴上点C反射后,经过点
B(6,2),则点C的坐标是 .
(2,0)
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
17.如图,在边长为9的正三角形ABC中,BD=3,∠ADE=60°,则AE的长为
.
7
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
18.如图,在平行四边形ABCD中,E为AB的中点,F为AD上一点,EF交AC
于点G,AF=2 cm,DF=4 cm,AG=3 cm,则AC的长为 .
15 cm
解析:延长FE,CB交于点H.∵四边形ABCD是平行四边形,∴BC=AD=6 cm,BC∥AD,∴∠EAF=∠EBH,∠AFE=∠BHE.∵AE=BE,∴△AFE △BHE,∴BH=AF=2 cm,∴CH=BC+BH=8 cm.∵BC∥AD,∴ = ,即 = ,解得CG=12,则AC=AG+CG=15 cm.
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
三、解答题(共66分) 19.(8分)已知线段a=3,b=8,c=6,d=4. (1)线段a,b,c,d是否成比例? (2)线段a,d,c,b是否成比例?
解:(1)∵3∶8≠6∶4, ∴线段a,b,c,d不成比例.
(2)∵3∶4=6∶8, ∴线段a,d,c,b成比例.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
20.(8分)如图,已知a∥b∥c,n,m分别与a,b,c交于点B,D,F和点A,C,E. (1)若AC=6 cm,CE=4 cm,BD=8 cm,求线段DF的长; (2)若AE∶CE=5∶2,BD=5 cm,求线段DF的长.
解:(1)∵a∥b∥c,∴ = , 即 = ,解得DF= .
(2)∵AE∶CE=5∶2,∴AC∶CE=3∶2. ∵a∥b∥c,∴ = = , 即 = ,解得DF= .
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
21.(8分)如图,在△ABC中,AD是中线,且CD2=BE?BA.求证:ED?AB=AD?BD.
证明:∵AD是中线, ∴BD=CD. ∵CD2=BE?BA, ∴BD2=BE?BA,即 = . 又∵∠B=∠B, ∴△BDE∽△BAD, ∴ = , ∴ED?AB=AD?BD.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
22.(10分)如图,在正方形ABCD中,点M,N分别在AB,BC上,AB=4,AM=1,
BN= . (1)求证:△ADM∽△BMN;
证明:∵四边形ABCD是正方形, ∴AD=AB=4,∠A=∠B=90°. ∵AM=1,∴BM=3, ∴ = = , = ,∴ = . 又∵∠A=∠B=90°, ∴△ADM∽△BMN.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
解:∵△ADM∽△BMN, ∴∠ADM=∠BMN. ∵∠ADM+∠AMD=90°, ∴∠AMD+∠BMN=90°, ∴∠DMN=180°-90°=90°.
(2)求∠DMN的度数.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
23.(10分)如图,在△ABC中,D是BC的中点,且AD=AC,DE⊥BC交AB于
点E,EC交AD于点F. (1)求证:△ABC∽△FCD;
证明:∵D是BC的中点,∴BD=CD. ∵DE⊥BC,∴∠BDE=∠CDE=90°. 又∵DE=DE,∴△BDE △CDE, ∴∠B=∠ECB. ∵AD=AC,∴∠ADC=∠ACB, ∴△ABC∽△FCD.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)求 的值.
解:∵△ABC∽△FCD, ∴ = . ∵D是BC的中点,∴BC=2CD,∴AD=AC=2FD. ∵∠ACD=∠ADC=∠B+∠EAD,∠B=∠FCD, ∴∠EAD=∠ACE,∴△EAF∽△ECA, ∴ = = = , ∴EC=2EA=4EF, ∴ =3.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
24.(10分)如图,P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD
于点E,交BA的延长线于点F. (1)求证:△APE∽△FPA;
证明:∵四边形ABCD是菱形, ∴AD=CD,∠ADP=∠CDP. 在△APD和△CPD中, ∴△APD △CPD(SAS),∴∠DAP=∠DCP. ∵CD∥BF,∴∠DCP=∠F,∴∠DAP=∠F. 又∵∠APE=∠FPA,∴△APE∽△FPA.
AD=CD,
∠ADP=∠CDP,
PD=PD,
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)若PE=2,EF=6,求PC的长.
解:∵△APE∽△FPA,∴ = ,∴PA2=PE?PF. ∵△APD △CPD,∴PA=PC,∴PC2=PE?PF. ∵PE=2,EF=6,∴PF=PE+EF=2+6=8,∴PC2=2×8=16, ∴PC=4.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
25.(12分)(1)问题:如图1,在四边形ABCD中,P为AB上一点,∠DPC=∠A
=∠B=90°,求证:AD?BC=AP?BP;
证明:∵∠DPC=∠A=∠B=90°, ∴∠ADP+∠APD=90°,∠BPC+∠APD=90°, ∴∠ADP=∠BPC,∴△ADP∽△BPC,
∴ = ,∴AD?BC=AP?BP.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)探究:如图2,在四边形ABCD中,P为AB上一点,当∠DPC=∠A=∠B=θ
时,上述结论是否依然成立?请说明理由;
解:结论AD?BC=AP?BP仍然成立.理由: ∵∠BPD=∠DPC+∠BPC,∠BPD=∠A+∠ADP, ∴∠DPC+∠BPC=∠A+∠ADP. ∵∠DPC=∠A=∠B=θ,∴∠BPC=∠ADP,∴△ADP∽△BPC, ∴ = ,∴AD?BC=AP?BP.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(3)应用:请利用(1)(2)获得的经验解决问题: 如图3,在△ABD中,AB=6,AD=BD=5,点P以每秒1个单位
长度的速度,由点A出发,沿边AB向点B运动,且满足∠CPD=
∠A.设点P的运动时间为t(秒),当DC=4BC时,求t的值.
解:∵DC=4BC, AD=BD=5,∴DC=4,BC=1. 由(1)(2)可知AD?BC=AP?BP, ∴5×1=t(6-t),解得t1=1,t2=5, ∴t的值为1或5.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
附加题(20分) 阅读材料,如图1, O中的任意两条弦AC,BD交于点P,若连接AB,CD,易证△ABP∽△DCP,则PA∶PD=PB∶PC,即PA·PC=PB·PD. 解决下列问题: (1)若PA=3PC=6,且P为BD中点,则BD= ;
上一栏目
附加题
(2)如图2,直线AB,CD交于点Q. ①求证:QA·QB=QC·QD;
①证明:∵四边形ABDC为圆内接四边形, ∴∠QAC=∠D. ∵∠Q=∠Q,∠QAC=∠D, ∴△QAC∽△QDB, ∴QA∶QD=QC∶QB, 即QA·QB=QC·QD.
上一栏目
附加题
②由①的结论可以猜想:当点A,B重合,即QA与 O相切于点A时,QA2=
QC·QD,作图并说明此猜想是否正确.
②解:作图略. QA与 O相切于点A,连接AO,并延长交 O于点N,连接CN. ∵QA与 O相切,∴AN⊥AQ,∴∠NAC+∠CAQ=90°. ∵AN为直径,∴∠ACN=90°,∴∠NAC+∠N=90°,∴∠CAQ=∠N. ∵ = ,∴∠N=∠D,∴∠CAQ=∠D.
∵∠Q=∠Q,∠CAQ=∠D,∴△QAC∽△QDA,∴QA∶QD=QC∶QA,
即QA2=QC·QD,∴此猜想正确.
上一栏目
附加题
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
