周周卷(七) 相似三角形的性质与应用及位拟 习题课件(34张PPT)
文档属性
| 名称 | 周周卷(七) 相似三角形的性质与应用及位拟 习题课件(34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 19:57:33 | ||
图片预览







文档简介
周周卷(七) 相似三角形的性质与应用及位拟
测试范围:27.2.2~27.3
选择题
填空题
附加题
解答题
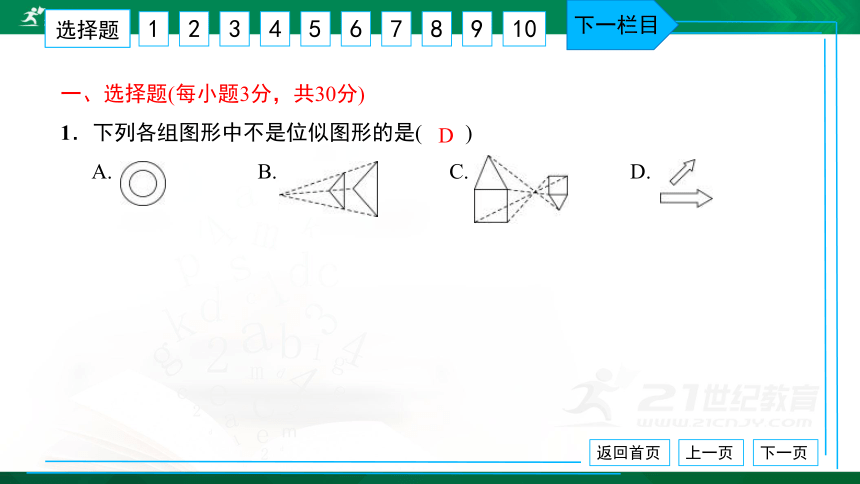
一、选择题(每小题3分,共30分) 1.下列各组图形中不是位似图形的是( ) A. B. C. D.
D
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
2.若△ABC与△DEF相似,且对应边的比为2∶3,则△ABC与△DEF的周长
比为( ) A.2∶5 B.2∶3 C.4∶9 D.4∶25
B
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
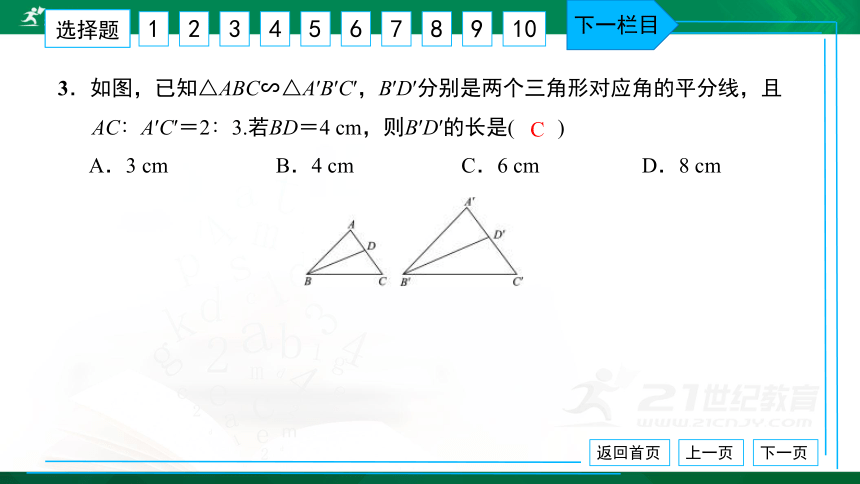
3.如图,已知△ABC∽△A′B′C′,B′D′分别是两个三角形对应角的平分线,且
AC∶A′C′=2∶3.若BD=4 cm,则B′D′的长是( ) A.3 cm B.4 cm C.6 cm D.8 cm
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
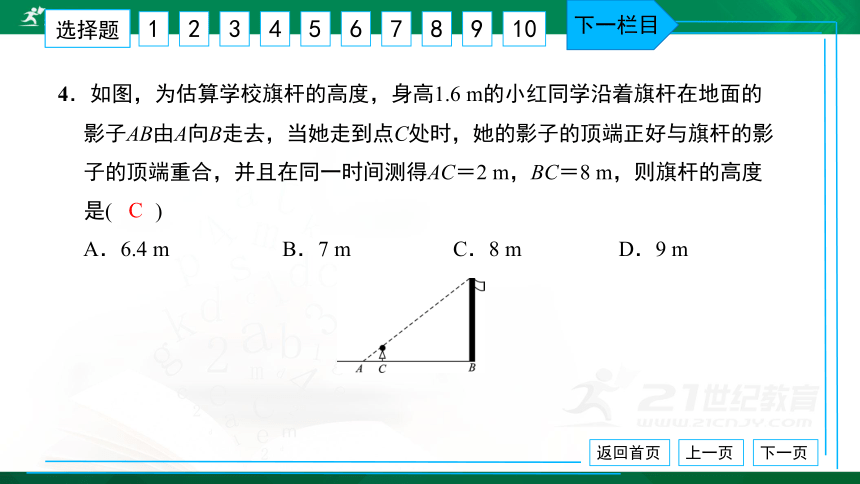
4.如图,为估算学校旗杆的高度,身高1.6 m的小红同学沿着旗杆在地面的
影子AB由A向B走去,当她走到点C处时,她的影子的顶端正好与旗杆的影
子的顶端重合,并且在同一时间测得AC=2 m,BC=8 m,则旗杆的高度
是( ) A.6.4 m B.7 m C.8 m D.9 m
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
5.已知△ABC∽△DEF,AB∶DE=1∶2,则下列等式一定成立的是( ) A. = B. = C. = D. =
D
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
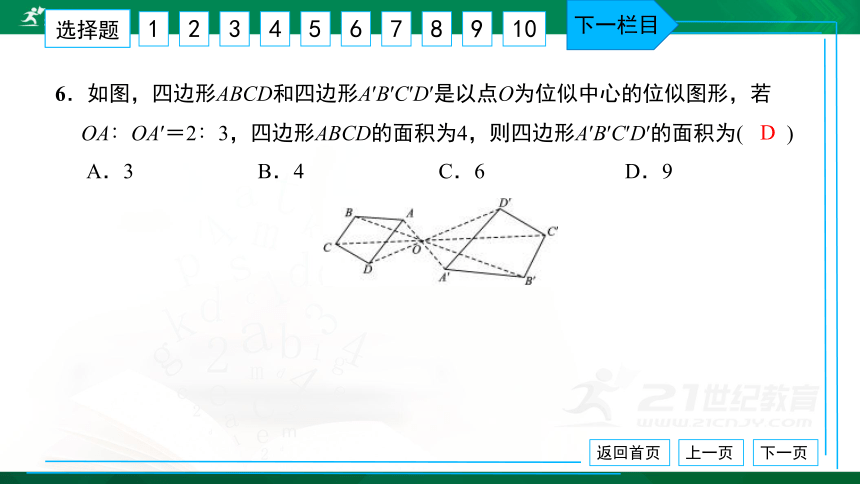
6.如图,四边形ABCD和四边形A′B′C′D′是以点O为位似中心的位似图形,若
OA∶OA′=2∶3,四边形ABCD的面积为4,则四边形A′B′C′D′的面积为( ) A.3 B.4 C.6 D.9
D
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
7.如图,一架投影机插入胶片后图像可投到屏幕上.已知胶片与屏幕平行,
点A为光源,与胶片BC的距离为0.1 m,胶片的高BC为0.038 m,若需要投影
后的图像DE高1.9 m,则投影机光源离屏幕大约为( ) A.6 m B.5 m C.4 m D.3 m
B
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
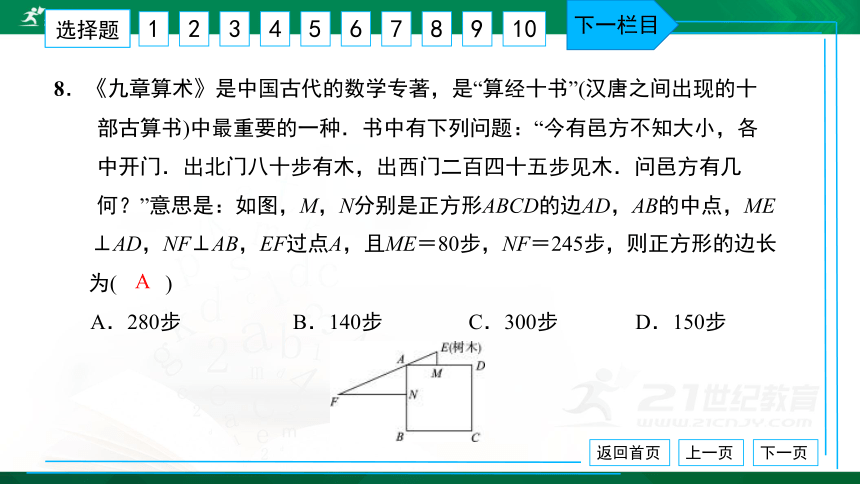
8.《九章算术》是中国古代的数学专著,是“算经十书”(汉唐之间出现的十
部古算书)中最重要的一种.书中有下列问题:“今有邑方不知大小,各
中开门.出北门八十步有木,出西门二百四十五步见木.问邑方有几
何?”意思是:如图,M,N分别是正方形ABCD的边AD,AB的中点,ME
⊥AD,NF⊥AB,EF过点A,且ME=80步,NF=245步,则正方形的边长
为( ) A.280步 B.140步 C.300步 D.150步
A
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
9.在平面直角坐标系中,△ABO顶点的坐标分别为A(-2,4),B(4,0),O(0,
0).以原点O为位似中心,把这个三角形缩小为原来的 得到△CDO,则
点A的对应点C的坐标是( ) A.(-4,8) B.(-4,8)或(4,-8) C.(-1,2) D.(-1,2)或(1,-2)
D
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
10.如图,有一块三角形余料ABC,已知BC=60 mm,高线AD=40 mm,要
把它加工成一个矩形零件,使矩形的一边在BC上,点P,M分别在AB,
AC上.若满足PM∶PQ=3∶2,则PM的长为( ) A. mm B. mm C.30 mm D.10 mm
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
二、填空题(每小题3分,共24分) 11.已知两个相似三角形的相似比为4∶3,则这两个三角形的对应高的比为
.
4∶3
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
12.如图,A,B两点间有一湖泊无法直接测量,已知CA=60 m,CD=24 m,
DE=32 m,DE∥AB,则AB= m.
80
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
13.如图,以点O为位似中心,将△OAB放大后得到△OCD,若OA=2,AC=
3,则 = .
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
14.如图,△DEF是由△ABC经过位似变换得到的,点O是位似中心,D,E,
F分别是OA,OB,OC的中点,则△DEF与△ABC的面积比是 .
1∶4
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
15.如果两个相似三角形周长的差是4,对应中线的比是4∶5,那么较大三角
形的周长是 .
20
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
16.如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,相似比
为1∶ ,若点A的坐标为(0,4),则点E的坐标为 .
(4 ,4 )
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
17.如图,小明在A时测得某树的影长为2 m,B时又测得该树的影长为8 m,
若两次日照的光线互相垂直,则树的高度为 m.
4
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
18.在△ABC中,AB=6,AC=5,点D,E分别在边AB,AC上,若△ADE与
△ABC相似,且S△ADE∶S四边形BCED=4∶21,则AD= .
2或
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
三、解答题(共66分) 19.(8分)已知△ABC∽△A′B′C′ , = ,AB边上的中线CD=4 cm,△A′B′C′
的面积是64 cm2. (1)求A′B′边上的中线C′D′的长;
解:∵△ABC∽△A′B′C′ , = ,CD=4 cm, ∴ = , ∴C′D′=8 cm.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)求△ABC的面积.
∵△ABC∽△A′B′C′, = ,△A′B′C′的面积是64 cm2, ∴ =( )2= , ∴S△ABC=16 cm2.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
20.(8分)如图,在13×13的网格图中,已知△ABC和点M(1,2). (1)以点M为位似中心,位似比为2,画出△ABC的位似图形△A′B′C′; (2)写出△A′B′C′的各顶点坐标.
解:(1)如图所示,△A′B′C′即为所作.
(2)△A′B′C′的各顶点坐标分别为A′(3,6),B′(5,2),C′(11,4).
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
21.(8分)如图,为了估算某条河的宽度,勘测人员在河的对岸选定一个目标点
A,在近岸分别取点B,D,E,C,使点A,B,D在一条直线上,且AD⊥DE,
点A,C,E也在一条直线上,且DE∥BC.经测量BC=24 m,BD=12 m,DE
=40 m,求河的宽度AB为多少米?
解:设宽度AB为x m. ∵DE∥BC,∴△ABC∽△ADE,∴ . ∵BC=24 m,BD=12 m,DE=40 m,
∴ , 解得x=18. 答:河的宽度为18 m.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
22.(10分)九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆
高度CD=3 m,标杆与旗杆的水平距离BD=15 m,人的眼睛与地面的高度
EF=1.6 m,人与标杆CD的水平距离DF=2 m,求旗杆AB的高度.
解:设EH与CD交于点G. ∵CD⊥FB,AB⊥FB,∴CD∥AB, ∴△CGE∽△AHE,∴ , 即 ,∴ , 解得AH=11.9, ∴AB=AH+HB=AH+EF=11.9+1.6=13.5(m), 即旗杆AB的高度为13.5 m.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
23.(10分)如图,矩形ABCD与矩形A′B′C′D′是位似图形,A是位似中心,已知
矩形ABCD的周长为24,BB′=4,DD′=2.求AB和AD的长.
解:设AB=x. ∵矩形ABCD的周长为24,∴AD=12-x. ∵BB′=4,DD′=2, ∴AD′=AD+DD′=14-x,AB′=AB+BB′=x+4. ∵矩形ABCD与矩形A′B′C′D′是位似图形, ∴ = ,即 = ,解得x=8. 经检验,x=8是原分式方程的解,∴AB=8,AD=4.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
24.(10分)如图,在相对的两栋楼中间有一堵墙,甲、乙两人分别在这两栋楼
内观察这堵墙,视线如图1所示.根据实际情况画出平面图形如图2(CD⊥
DF,AB⊥DF,EF⊥DF),甲从点C可以看到点G处,乙从点E可以看到点
D处,B是DF的中点,墙AB高5.5米,DF=100米,BG=10.5米,求甲、乙
两人的观测点到地面的距离之差(结果精确到0.1米)
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
解:由题意可知∠ABG=∠CDG=90°. ∵∠AGD为公共角,∴△ABG∽△CDG,∴ = . ∵DF=100米,B是DF的中点,∴BD=BF=50米. ∵AB=5.5米,BG=10.5米,∴ = ,解得CD≈31.69米. ∵∠ABD=∠EFD=90°,∠EDF为公共角, ∴△ADB∽△EDF,∴ = = , ∴EF=2AB=11米, ∴CD-EF≈20.7米. 答:甲、乙两人的观测点到地面的距离之差约为20.7米.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
25.(12分)如图,在△ABC中,AB=5,BC=3,AC=4,动点E(与点A,C不
重合)在AC边上,EF∥AB交BC于点F. (1)当△ECF的面积与四边形EABF的面积相等时,求CE的长;
解:∵△ECF的面积与四边形EABF的面积相等, ∴S△ECF∶S△ACB=1∶2. ∵EF∥AB, ∴△ECF∽△ACB, ∴ =( )2= . ∵AC=4,∴CE=2 .
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)当△ECF的周长与四边形EABF的周长相等时,求CE的长.
设CE的长为x. ∵△ECF∽△ACB, ∴ = ,∴CF= x. 由△ECF的周长与四边形EABF的周长相等, 得x+EF+ x=(4-x)+5+(3- x)+EF,解得x= , ∴CE的长为 .
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
附加题(20分) 课本中有一道作业题:有一块三角形余料ABC,它的边BC=120 mm,高AD=80 mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上. (1)求加工成的正方形零件的边长;
解:设正方形的边长为x mm, 则PN=PQ=ED=x,AE=AD-ED=80-x. ∵PN∥BC,∴△APN∽△ABC,∴ = , 即 = ,解得x=48. ∴加工成的正方形零件的边长是48 mm.
上一栏目
附加题
(2)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方
形所组成,如图1,此时这个矩形零件的两条边长又分别为多少?
设PQ=x,则PN=2x,AE=80-x. ∵PN∥BC,∴△APN∽△ABC, ∴ = ,即 = ,解得x= , ∴2x= , ∴这个矩形零件的两条边长分别为 mm, mm.
上一栏目
附加题
(3)如果原题中所要加工的零件只是一个矩形,如图2,这样此矩形零件的两
条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩
形零件的两条边长.
设PN=x,矩形PQMN的面积为S. ∵PN∥BC,∴△APN∽△ABC,∴ = , 即 = ,解得PQ=80- x, 则S=PN·PQ=x(80- x)=- x2+80x=- (x-60)2+2400, 故S的最大值为2400 mm2, 此时PN=60 mm,PQ=80- ×60=40(mm).
上一栏目
附加题
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
测试范围:27.2.2~27.3
选择题
填空题
附加题
解答题
一、选择题(每小题3分,共30分) 1.下列各组图形中不是位似图形的是( ) A. B. C. D.
D
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
2.若△ABC与△DEF相似,且对应边的比为2∶3,则△ABC与△DEF的周长
比为( ) A.2∶5 B.2∶3 C.4∶9 D.4∶25
B
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
3.如图,已知△ABC∽△A′B′C′,B′D′分别是两个三角形对应角的平分线,且
AC∶A′C′=2∶3.若BD=4 cm,则B′D′的长是( ) A.3 cm B.4 cm C.6 cm D.8 cm
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
4.如图,为估算学校旗杆的高度,身高1.6 m的小红同学沿着旗杆在地面的
影子AB由A向B走去,当她走到点C处时,她的影子的顶端正好与旗杆的影
子的顶端重合,并且在同一时间测得AC=2 m,BC=8 m,则旗杆的高度
是( ) A.6.4 m B.7 m C.8 m D.9 m
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
5.已知△ABC∽△DEF,AB∶DE=1∶2,则下列等式一定成立的是( ) A. = B. = C. = D. =
D
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
6.如图,四边形ABCD和四边形A′B′C′D′是以点O为位似中心的位似图形,若
OA∶OA′=2∶3,四边形ABCD的面积为4,则四边形A′B′C′D′的面积为( ) A.3 B.4 C.6 D.9
D
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
7.如图,一架投影机插入胶片后图像可投到屏幕上.已知胶片与屏幕平行,
点A为光源,与胶片BC的距离为0.1 m,胶片的高BC为0.038 m,若需要投影
后的图像DE高1.9 m,则投影机光源离屏幕大约为( ) A.6 m B.5 m C.4 m D.3 m
B
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
8.《九章算术》是中国古代的数学专著,是“算经十书”(汉唐之间出现的十
部古算书)中最重要的一种.书中有下列问题:“今有邑方不知大小,各
中开门.出北门八十步有木,出西门二百四十五步见木.问邑方有几
何?”意思是:如图,M,N分别是正方形ABCD的边AD,AB的中点,ME
⊥AD,NF⊥AB,EF过点A,且ME=80步,NF=245步,则正方形的边长
为( ) A.280步 B.140步 C.300步 D.150步
A
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
9.在平面直角坐标系中,△ABO顶点的坐标分别为A(-2,4),B(4,0),O(0,
0).以原点O为位似中心,把这个三角形缩小为原来的 得到△CDO,则
点A的对应点C的坐标是( ) A.(-4,8) B.(-4,8)或(4,-8) C.(-1,2) D.(-1,2)或(1,-2)
D
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
10.如图,有一块三角形余料ABC,已知BC=60 mm,高线AD=40 mm,要
把它加工成一个矩形零件,使矩形的一边在BC上,点P,M分别在AB,
AC上.若满足PM∶PQ=3∶2,则PM的长为( ) A. mm B. mm C.30 mm D.10 mm
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
二、填空题(每小题3分,共24分) 11.已知两个相似三角形的相似比为4∶3,则这两个三角形的对应高的比为
.
4∶3
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
12.如图,A,B两点间有一湖泊无法直接测量,已知CA=60 m,CD=24 m,
DE=32 m,DE∥AB,则AB= m.
80
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
13.如图,以点O为位似中心,将△OAB放大后得到△OCD,若OA=2,AC=
3,则 = .
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
14.如图,△DEF是由△ABC经过位似变换得到的,点O是位似中心,D,E,
F分别是OA,OB,OC的中点,则△DEF与△ABC的面积比是 .
1∶4
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
15.如果两个相似三角形周长的差是4,对应中线的比是4∶5,那么较大三角
形的周长是 .
20
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
16.如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,相似比
为1∶ ,若点A的坐标为(0,4),则点E的坐标为 .
(4 ,4 )
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
17.如图,小明在A时测得某树的影长为2 m,B时又测得该树的影长为8 m,
若两次日照的光线互相垂直,则树的高度为 m.
4
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
18.在△ABC中,AB=6,AC=5,点D,E分别在边AB,AC上,若△ADE与
△ABC相似,且S△ADE∶S四边形BCED=4∶21,则AD= .
2或
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
三、解答题(共66分) 19.(8分)已知△ABC∽△A′B′C′ , = ,AB边上的中线CD=4 cm,△A′B′C′
的面积是64 cm2. (1)求A′B′边上的中线C′D′的长;
解:∵△ABC∽△A′B′C′ , = ,CD=4 cm, ∴ = , ∴C′D′=8 cm.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)求△ABC的面积.
∵△ABC∽△A′B′C′, = ,△A′B′C′的面积是64 cm2, ∴ =( )2= , ∴S△ABC=16 cm2.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
20.(8分)如图,在13×13的网格图中,已知△ABC和点M(1,2). (1)以点M为位似中心,位似比为2,画出△ABC的位似图形△A′B′C′; (2)写出△A′B′C′的各顶点坐标.
解:(1)如图所示,△A′B′C′即为所作.
(2)△A′B′C′的各顶点坐标分别为A′(3,6),B′(5,2),C′(11,4).
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
21.(8分)如图,为了估算某条河的宽度,勘测人员在河的对岸选定一个目标点
A,在近岸分别取点B,D,E,C,使点A,B,D在一条直线上,且AD⊥DE,
点A,C,E也在一条直线上,且DE∥BC.经测量BC=24 m,BD=12 m,DE
=40 m,求河的宽度AB为多少米?
解:设宽度AB为x m. ∵DE∥BC,∴△ABC∽△ADE,∴ . ∵BC=24 m,BD=12 m,DE=40 m,
∴ , 解得x=18. 答:河的宽度为18 m.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
22.(10分)九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆
高度CD=3 m,标杆与旗杆的水平距离BD=15 m,人的眼睛与地面的高度
EF=1.6 m,人与标杆CD的水平距离DF=2 m,求旗杆AB的高度.
解:设EH与CD交于点G. ∵CD⊥FB,AB⊥FB,∴CD∥AB, ∴△CGE∽△AHE,∴ , 即 ,∴ , 解得AH=11.9, ∴AB=AH+HB=AH+EF=11.9+1.6=13.5(m), 即旗杆AB的高度为13.5 m.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
23.(10分)如图,矩形ABCD与矩形A′B′C′D′是位似图形,A是位似中心,已知
矩形ABCD的周长为24,BB′=4,DD′=2.求AB和AD的长.
解:设AB=x. ∵矩形ABCD的周长为24,∴AD=12-x. ∵BB′=4,DD′=2, ∴AD′=AD+DD′=14-x,AB′=AB+BB′=x+4. ∵矩形ABCD与矩形A′B′C′D′是位似图形, ∴ = ,即 = ,解得x=8. 经检验,x=8是原分式方程的解,∴AB=8,AD=4.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
24.(10分)如图,在相对的两栋楼中间有一堵墙,甲、乙两人分别在这两栋楼
内观察这堵墙,视线如图1所示.根据实际情况画出平面图形如图2(CD⊥
DF,AB⊥DF,EF⊥DF),甲从点C可以看到点G处,乙从点E可以看到点
D处,B是DF的中点,墙AB高5.5米,DF=100米,BG=10.5米,求甲、乙
两人的观测点到地面的距离之差(结果精确到0.1米)
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
解:由题意可知∠ABG=∠CDG=90°. ∵∠AGD为公共角,∴△ABG∽△CDG,∴ = . ∵DF=100米,B是DF的中点,∴BD=BF=50米. ∵AB=5.5米,BG=10.5米,∴ = ,解得CD≈31.69米. ∵∠ABD=∠EFD=90°,∠EDF为公共角, ∴△ADB∽△EDF,∴ = = , ∴EF=2AB=11米, ∴CD-EF≈20.7米. 答:甲、乙两人的观测点到地面的距离之差约为20.7米.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
25.(12分)如图,在△ABC中,AB=5,BC=3,AC=4,动点E(与点A,C不
重合)在AC边上,EF∥AB交BC于点F. (1)当△ECF的面积与四边形EABF的面积相等时,求CE的长;
解:∵△ECF的面积与四边形EABF的面积相等, ∴S△ECF∶S△ACB=1∶2. ∵EF∥AB, ∴△ECF∽△ACB, ∴ =( )2= . ∵AC=4,∴CE=2 .
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)当△ECF的周长与四边形EABF的周长相等时,求CE的长.
设CE的长为x. ∵△ECF∽△ACB, ∴ = ,∴CF= x. 由△ECF的周长与四边形EABF的周长相等, 得x+EF+ x=(4-x)+5+(3- x)+EF,解得x= , ∴CE的长为 .
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
附加题(20分) 课本中有一道作业题:有一块三角形余料ABC,它的边BC=120 mm,高AD=80 mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上. (1)求加工成的正方形零件的边长;
解:设正方形的边长为x mm, 则PN=PQ=ED=x,AE=AD-ED=80-x. ∵PN∥BC,∴△APN∽△ABC,∴ = , 即 = ,解得x=48. ∴加工成的正方形零件的边长是48 mm.
上一栏目
附加题
(2)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方
形所组成,如图1,此时这个矩形零件的两条边长又分别为多少?
设PQ=x,则PN=2x,AE=80-x. ∵PN∥BC,∴△APN∽△ABC, ∴ = ,即 = ,解得x= , ∴2x= , ∴这个矩形零件的两条边长分别为 mm, mm.
上一栏目
附加题
(3)如果原题中所要加工的零件只是一个矩形,如图2,这样此矩形零件的两
条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩
形零件的两条边长.
设PN=x,矩形PQMN的面积为S. ∵PN∥BC,∴△APN∽△ABC,∴ = , 即 = ,解得PQ=80- x, 则S=PN·PQ=x(80- x)=- x2+80x=- (x-60)2+2400, 故S的最大值为2400 mm2, 此时PN=60 mm,PQ=80- ×60=40(mm).
上一栏目
附加题
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
