专题卷(六) 相似三角形的判定与性质的综合运用 习题课件(20张PPT)
文档属性
| 名称 | 专题卷(六) 相似三角形的判定与性质的综合运用 习题课件(20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 00:00:00 | ||
图片预览




文档简介
专题卷(六) 相似三角形的判定与性质的综合运用
类型一
类型二
类型三
类型四
类型一 利用相似三角形求线段长 1.如图,在△ABC中,∠ABD=∠C,若AB=4,AD=2,则CD的长是( ) A.2 B.4 C.6 D.8
C
类型一
1
2
3
4
下一栏目
2.如图,在矩形ABCD中,AB=3,BC=4,点M在BC边上,且满足BM=1,
过点D作DN⊥AM交AM于点N,则DN的长为( ) A. B. C. D.
D
类型一
1
2
3
4
下一栏目
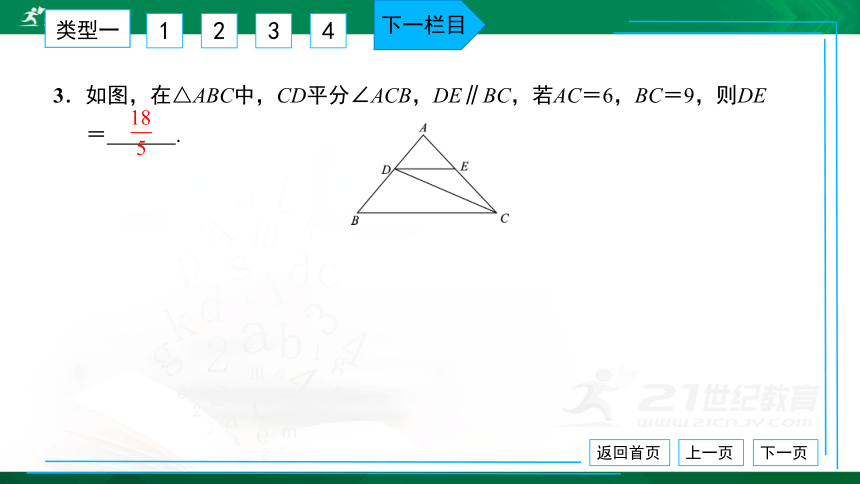
3.如图,在△ABC中,CD平分∠ACB,DE∥BC,若AC=6,BC=9,则DE
= .
类型一
1
2
3
4
下一栏目
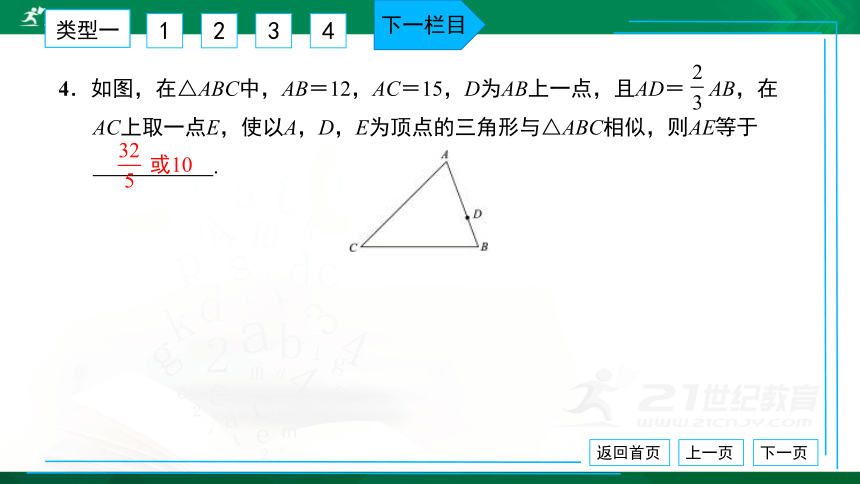
4.如图,在△ABC中,AB=12,AC=15,D为AB上一点,且AD= AB,在
AC上取一点E,使以A,D,E为顶点的三角形与△ABC相似,则AE等于
.
或10
类型一
1
2
3
4
下一栏目
5.如图,AB=3,AC=2,BC=4,AE=3,AD=4.5,DE=6,∠BAD=20°,
则∠CAE的度数为( ) A.10° B.20° C.40° D.无法确定
类型二 利用相似三角形求角度
B
上一栏目
类型二
5
6
7
下一栏目
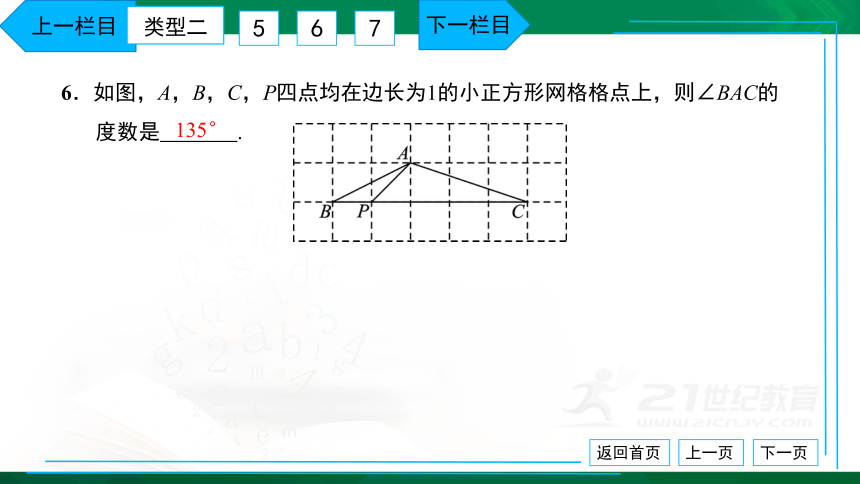
6.如图,A,B,C,P四点均在边长为1的小正方形网格格点上,则∠BAC的
度数是 .
135°
上一栏目
类型二
5
6
7
下一栏目
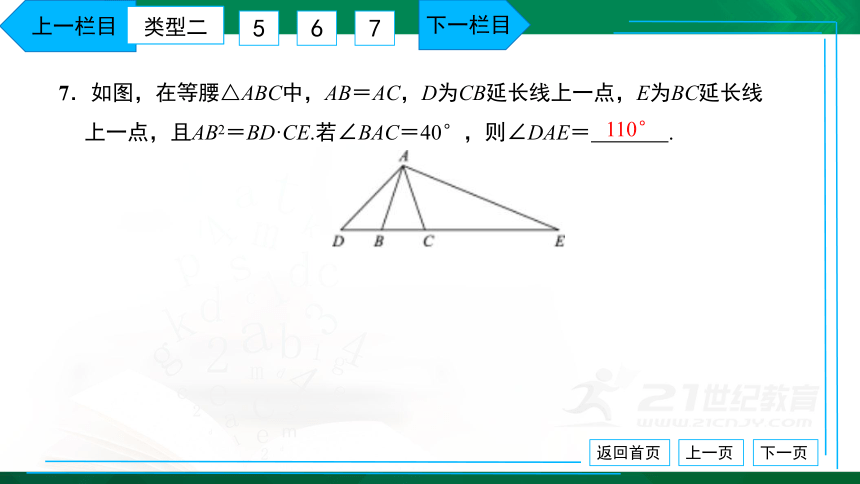
7.如图,在等腰△ABC中,AB=AC,D为CB延长线上一点,E为BC延长线
上一点,且AB2=BD·CE.若∠BAC=40°,则∠DAE= .
110°
上一栏目
类型二
5
6
7
下一栏目
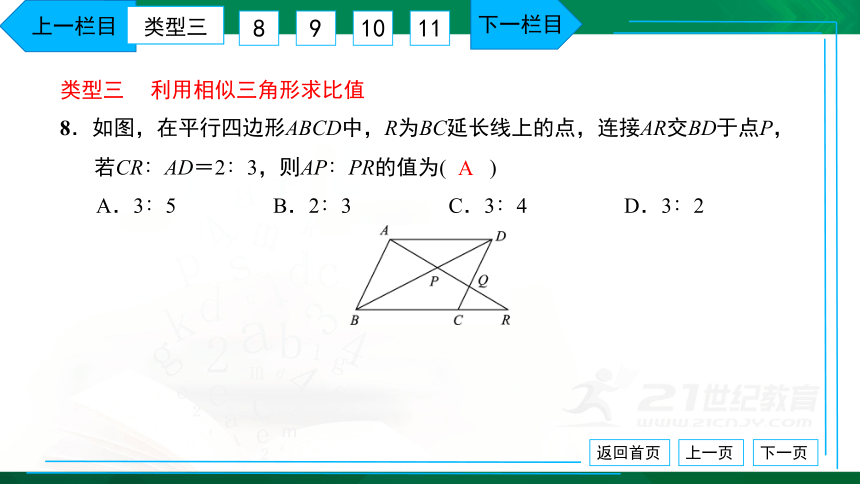
类型三 利用相似三角形求比值 8.如图,在平行四边形ABCD中,R为BC延长线上的点,连接AR交BD于点P,
若CR∶AD=2∶3,则AP∶PR的值为( ) A.3∶5 B.2∶3 C.3∶4 D.3∶2
A
上一栏目
类型三
8
9
10
下一栏目
11
9.如图,DE∥BC,DE将△ABC分成面积相等的两部分,那么 的值为
( ) A. -1 B. C.1 D. +1
B
上一栏目
类型三
8
9
10
下一栏目
11
10.如图,在正方形ABCD中,点E,F,G分别在边AD,AB,BC上,DE=
2AE,BF=2AF,BG=2CG,则 的值为( ) A. B. C. D.
B
上一栏目
类型三
8
9
10
下一栏目
11
11.如图,在菱形ABCD中,EF⊥AC,垂足为点H,分别交AD,AB及CB的延
长线于点E,M,F,且AE∶FB=1∶2,则AH∶AC的值为( ) A. B. C. D.
B
上一栏目
类型三
8
9
10
下一栏目
11
类型四 利用相似三角形计算与证明 12.如图,在△ABC中.AB=AC,AD⊥BC于点D,作DE⊥AC于点E,F是AB
的中点,连EF交AD于点G. (1)求证:AD2=AB?AE;
证明:∵AD⊥BC,DE⊥AC,∴∠ADC=∠AED=90°. ∵∠DAE=∠DAC,∴△DAE∽△CAD, ∴ = ,∴AD2=AC?AE. ∵AC=AB,∴AD2=AB?AE.
上一栏目
类型四
12
13
14
(2)若AB=3,AE=2,求 的值.
解:连接DF. ∵AB=3,∠ADB=90°,F是AB的中点, ∴DF= AB= . ∵AB=AC,AD⊥BC,∴BD=DC,∴DF∥AC, ∴ = = = ,∴ = .
上一栏目
类型四
12
13
14
13.如图,在平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,
DE= CD. (1)求证:△ABF∽△CEB;
证明:∵四边形ABCD是平行四边形, ∴∠A=∠C,AB∥CD, ∴∠ABF=∠CEB, ∴△ABF∽△CEB.
上一栏目
类型四
12
13
14
(2)若△DEF的面积为2,求四边形BCDF的面积.
解:∵四边形ABCD是平行四边形, ∴AD∥BC, ∴△DEF∽△CEB. ∵DE= CD,∴ = ,∴ = = . ∵S△DEF=2,∴S△CEB=18, ∴S四边形BCDF=S△BCE-S△DEF=16.
上一栏目
类型四
12
13
14
14.如图,在△ABC与△ADE中,∠ACB=∠AED=90°,连接BD,CE,∠EAC
=∠DAB. (1)求证:△ABC∽△ADE; (2)求证:△BAD∽△CAE;
(1)证明:∵∠EAC=∠DAB,∴∠CAB=∠EAD. 又∵∠ACB=∠AED=90°,∴△ABC∽△ADE.
(2)证明:由(1)知△ABC∽△ADE, ∴ = . ∵∠EAC=∠BAD,∴△BAD∽△CAE.
上一栏目
类型四
12
13
14
(3)已知BC=4,AC=3,AE= ,将△AED绕点A旋转,当点E落在线段CD上
时,求BD的长.
解:∵∠ACB=90°,BC=4,AC=3, ∴AB= = =5. ∵△ABC∽△ADE,∴ = ,
∴AD= = . 如图,将△AED绕点A旋转,当点E落在线段CD上时,∠AEC=∠ADB=90°, ∴BD= = = .
上一栏目
类型四
12
13
14
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
类型一
类型二
类型三
类型四
类型一 利用相似三角形求线段长 1.如图,在△ABC中,∠ABD=∠C,若AB=4,AD=2,则CD的长是( ) A.2 B.4 C.6 D.8
C
类型一
1
2
3
4
下一栏目
2.如图,在矩形ABCD中,AB=3,BC=4,点M在BC边上,且满足BM=1,
过点D作DN⊥AM交AM于点N,则DN的长为( ) A. B. C. D.
D
类型一
1
2
3
4
下一栏目
3.如图,在△ABC中,CD平分∠ACB,DE∥BC,若AC=6,BC=9,则DE
= .
类型一
1
2
3
4
下一栏目
4.如图,在△ABC中,AB=12,AC=15,D为AB上一点,且AD= AB,在
AC上取一点E,使以A,D,E为顶点的三角形与△ABC相似,则AE等于
.
或10
类型一
1
2
3
4
下一栏目
5.如图,AB=3,AC=2,BC=4,AE=3,AD=4.5,DE=6,∠BAD=20°,
则∠CAE的度数为( ) A.10° B.20° C.40° D.无法确定
类型二 利用相似三角形求角度
B
上一栏目
类型二
5
6
7
下一栏目
6.如图,A,B,C,P四点均在边长为1的小正方形网格格点上,则∠BAC的
度数是 .
135°
上一栏目
类型二
5
6
7
下一栏目
7.如图,在等腰△ABC中,AB=AC,D为CB延长线上一点,E为BC延长线
上一点,且AB2=BD·CE.若∠BAC=40°,则∠DAE= .
110°
上一栏目
类型二
5
6
7
下一栏目
类型三 利用相似三角形求比值 8.如图,在平行四边形ABCD中,R为BC延长线上的点,连接AR交BD于点P,
若CR∶AD=2∶3,则AP∶PR的值为( ) A.3∶5 B.2∶3 C.3∶4 D.3∶2
A
上一栏目
类型三
8
9
10
下一栏目
11
9.如图,DE∥BC,DE将△ABC分成面积相等的两部分,那么 的值为
( ) A. -1 B. C.1 D. +1
B
上一栏目
类型三
8
9
10
下一栏目
11
10.如图,在正方形ABCD中,点E,F,G分别在边AD,AB,BC上,DE=
2AE,BF=2AF,BG=2CG,则 的值为( ) A. B. C. D.
B
上一栏目
类型三
8
9
10
下一栏目
11
11.如图,在菱形ABCD中,EF⊥AC,垂足为点H,分别交AD,AB及CB的延
长线于点E,M,F,且AE∶FB=1∶2,则AH∶AC的值为( ) A. B. C. D.
B
上一栏目
类型三
8
9
10
下一栏目
11
类型四 利用相似三角形计算与证明 12.如图,在△ABC中.AB=AC,AD⊥BC于点D,作DE⊥AC于点E,F是AB
的中点,连EF交AD于点G. (1)求证:AD2=AB?AE;
证明:∵AD⊥BC,DE⊥AC,∴∠ADC=∠AED=90°. ∵∠DAE=∠DAC,∴△DAE∽△CAD, ∴ = ,∴AD2=AC?AE. ∵AC=AB,∴AD2=AB?AE.
上一栏目
类型四
12
13
14
(2)若AB=3,AE=2,求 的值.
解:连接DF. ∵AB=3,∠ADB=90°,F是AB的中点, ∴DF= AB= . ∵AB=AC,AD⊥BC,∴BD=DC,∴DF∥AC, ∴ = = = ,∴ = .
上一栏目
类型四
12
13
14
13.如图,在平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,
DE= CD. (1)求证:△ABF∽△CEB;
证明:∵四边形ABCD是平行四边形, ∴∠A=∠C,AB∥CD, ∴∠ABF=∠CEB, ∴△ABF∽△CEB.
上一栏目
类型四
12
13
14
(2)若△DEF的面积为2,求四边形BCDF的面积.
解:∵四边形ABCD是平行四边形, ∴AD∥BC, ∴△DEF∽△CEB. ∵DE= CD,∴ = ,∴ = = . ∵S△DEF=2,∴S△CEB=18, ∴S四边形BCDF=S△BCE-S△DEF=16.
上一栏目
类型四
12
13
14
14.如图,在△ABC与△ADE中,∠ACB=∠AED=90°,连接BD,CE,∠EAC
=∠DAB. (1)求证:△ABC∽△ADE; (2)求证:△BAD∽△CAE;
(1)证明:∵∠EAC=∠DAB,∴∠CAB=∠EAD. 又∵∠ACB=∠AED=90°,∴△ABC∽△ADE.
(2)证明:由(1)知△ABC∽△ADE, ∴ = . ∵∠EAC=∠BAD,∴△BAD∽△CAE.
上一栏目
类型四
12
13
14
(3)已知BC=4,AC=3,AE= ,将△AED绕点A旋转,当点E落在线段CD上
时,求BD的长.
解:∵∠ACB=90°,BC=4,AC=3, ∴AB= = =5. ∵△ABC∽△ADE,∴ = ,
∴AD= = . 如图,将△AED绕点A旋转,当点E落在线段CD上时,∠AEC=∠ADB=90°, ∴BD= = = .
上一栏目
类型四
12
13
14
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
