专题卷(五) 相似三角形与解直角三角形的实际应用 习题课件(共17张PPT)
文档属性
| 名称 | 专题卷(五) 相似三角形与解直角三角形的实际应用 习题课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 18:32:15 | ||
图片预览





文档简介
专题卷(五) 相似三角形与解直角三角形的实际应用
类型一
类型二
类型一 相似三角形的实际应用 1.如图,小芳在打网球时,为使球恰好能过网(网高0.8米),且落在对方区域
内离网5米的位置上,若她的击球高度是2.4米,则应站在离网( ) A.15米处 B.10米处 C.8米处 D.7.5米处
B
类型一
1
2
3
4
5
6
下一栏目
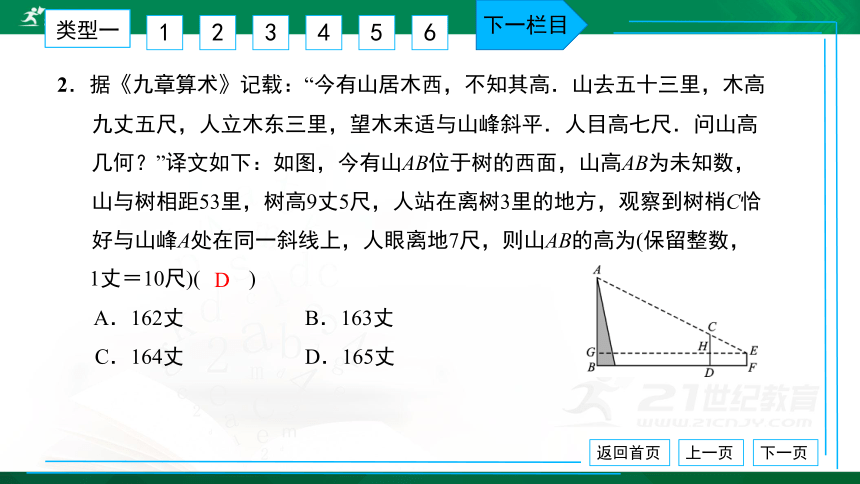
2.据《九章算术》记载:“今有山居木西,不知其高.山去五十三里,木高
九丈五尺,人立木东三里,望木末适与山峰斜平.人目高七尺.问山高
几何?”译文如下:如图,今有山AB位于树的西面,山高AB为未知数,
山与树相距53里,树高9丈5尺,人站在离树3里的地方,观察到树梢C恰
好与山峰A处在同一斜线上,人眼离地7尺,则山AB的高为(保留整数,
1丈=10尺)( ) A.162丈 B.163丈 C.164丈 D.165丈
D
类型一
1
2
3
4
5
6
下一栏目
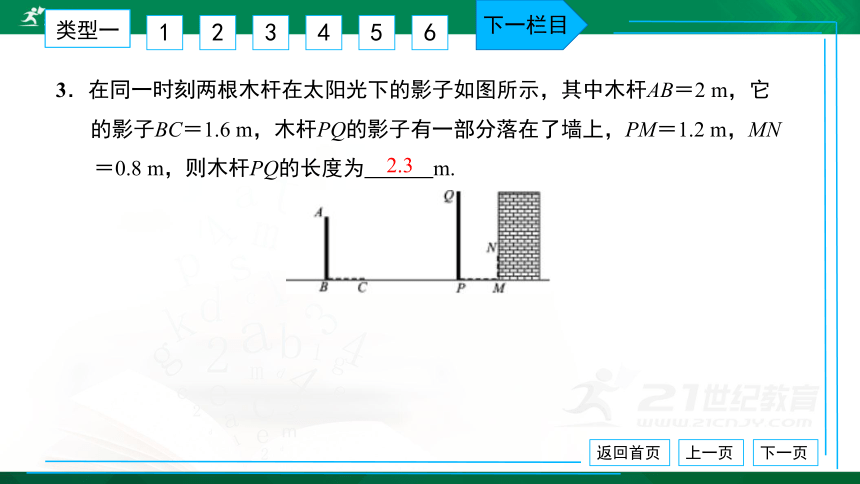
3.在同一时刻两根木杆在太阳光下的影子如图所示,其中木杆AB=2 m,它
的影子BC=1.6 m,木杆PQ的影子有一部分落在了墙上,PM=1.2 m,MN
=0.8 m,则木杆PQ的长度为 m.
2.3
类型一
1
2
3
4
5
6
下一栏目
4.如图所示为某种型号的台灯的横截面图,已知台灯灯柱AB长为30 cm,且
与水平桌面垂直,灯臂AC长为10 cm,灯头的横截面△CEF为直角三角形,
当灯臂AC与灯柱AB垂直时,沿CE边射出的光线刚好射到底座点B处.若
不考虑其他因素,则该台灯在桌面上可照亮的宽度BD的长为 cm.
100
类型一
1
2
3
4
5
6
下一栏目
5.如图,小明要测量操场旗杆高度AH,立两根高1米的标杆BC和DE,两标杆
相距BD=15米,点D,B,H在一条直线上,小明从BC退行2米到点F处,
着地观察A,C,F三点共线;从DE退行3米步到G,着地观察,A,E,G三
点也共线.则旗杆的高度AH为 米,HB的长度为 米.
16
30
类型一
1
2
3
4
5
6
下一栏目
6.如图1是一把落地遮阳伞,伞柄CD垂直于水平地面GQ,当点P与点A重合
时,伞收紧;当点P由点A向点B移动时,伞慢慢撑开;当点P与点B重合时,
伞完全张开.已知遮阳伞的高度CD=220 cm,在它撑开的过程中,总有
PM=PN=CM=CN=50 cm,CE=CF=120 cm,BC=20 cm. (1)当∠CPN=53°时,求BP的长;
解:连接MN,交CD于点H. ∵CM=MP=NC=NP=50 cm,∴四边形PMCN是菱形, ∴CP⊥MN,CH=PH, ∴PH=PN·cos53°≈30(cm),PC=2PH=60 cm, ∴PB=PC-BC=40 cm.
类型一
1
2
3
4
5
6
下一栏目
(2)如图2,当伞完全张开时,求点E到地面GQ的距离.(参考数据:sin53°≈0.8,
cos53°≈0.6,tan53°≈1.3)
连接MN交CD于点J,连接EF交CD于点H. ∵四边形CMBN是菱形,∴CJ=JB=10 cm. ∵MJ∥EH,∴△CMJ∽△CEH, ∴ = ,即 = , ∴CH=24 cm, ∴HD=CD-CH=220-24=196(cm), 即当伞完全张开时,点E到地面GQ的距离为196 cm.
类型一
1
2
3
4
5
6
下一栏目
类型二 解直角三角形的实际应用 7.如图,活动课上小明利用一个锐角是30°的三角板测量一棵树的高度,已
知他与树之间的水平距离BE=9 m,AB=1.5 m(即小明的眼睛距地面的距
离),那么这棵树高是( ) A.3 m B.27 m C.(3 +1.5) m D.(27 +1.5)m
C
上一栏目
类型二
7
8
9
10
11
8.如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为30°,测得底部C
的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为60 m,那么该
建筑物的高度BC为( ) A.80 m B.60 m C.80 m D.60 m
C
上一栏目
类型二
7
8
9
10
11
9.如图,一个直角梯形的堤坝坡长AB为6米,斜坡AB的坡角为60°,为了
改善堤坝的稳固性,准备将其坡角改为45°,则调整后的斜坡AE的长度
为( ) A.3 米 B.3 米 C.(3 -2)米 D.(3 -3)米
A
上一栏目
类型二
7
8
9
10
11
10.如图,一艘海上巡逻船在A地巡航,这时接到B地海上指挥中心紧急通知:
在指挥中心北偏西60°方向的C地,有一艘渔船遇险,要求马上前去救
援.此时C地位于A北偏西30°方向上,A地位于B地北偏西75°方向上,
A,B两地之间的距离为12海里.求A,C两地之间的距离.(参考数据:
≈1.41, ≈1.73, ≈2.45,结果精确到0.1海里)
上一栏目
类型二
7
8
9
10
11
解:过点B作BD⊥CA,交CA延长线于点D. 由题意,得∠ACB=60°-30°=30°, ∠ABC=75°-60°=15°,∴∠DAB=∠DBA=45°. 在Rt△ABD中, ∵AB=12,∠DAB=45°,
∴BD=AD=ABcos45°=6 . 在Rt△CBD中,CD= =6 , ∴AC=6 -6 ≈6.2(海里). 答:A,C两地之间的距离约为6.2海里.
上一栏目
类型二
7
8
9
10
11
11.如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上
走到P处再测得点C的仰角为45°,已知OA=100米,山坡坡度(竖直高度
与水平宽度的比)i=1∶2,且点O,A,B在同一条直线上.求电视塔OC
的高度以及此人所在位置点P的铅直高度.(结果保留根号形式)
上一栏目
类型二
7
8
9
10
11
解:过点P作PE⊥OB于点E,作PF⊥CO于点F. 在Rt△AOC中, ∵AO=100米,∠CAO=60°,∴CO=AO?tan60°=100 (米). 设PE=x米, ∵tan∠PAB= = ,∴AE=2x米. 在Rt△PCF中, ∠CPF=45°,CF=(100 -x)米,PF=OA+AE=(100+2x)米. ∵PF=CF,∴100+2x=100 -x,解得x= . 答:电视塔OC高为100 米,点P的铅直高度为 米.
上一栏目
类型二
7
8
9
10
11
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
类型一
类型二
类型一 相似三角形的实际应用 1.如图,小芳在打网球时,为使球恰好能过网(网高0.8米),且落在对方区域
内离网5米的位置上,若她的击球高度是2.4米,则应站在离网( ) A.15米处 B.10米处 C.8米处 D.7.5米处
B
类型一
1
2
3
4
5
6
下一栏目
2.据《九章算术》记载:“今有山居木西,不知其高.山去五十三里,木高
九丈五尺,人立木东三里,望木末适与山峰斜平.人目高七尺.问山高
几何?”译文如下:如图,今有山AB位于树的西面,山高AB为未知数,
山与树相距53里,树高9丈5尺,人站在离树3里的地方,观察到树梢C恰
好与山峰A处在同一斜线上,人眼离地7尺,则山AB的高为(保留整数,
1丈=10尺)( ) A.162丈 B.163丈 C.164丈 D.165丈
D
类型一
1
2
3
4
5
6
下一栏目
3.在同一时刻两根木杆在太阳光下的影子如图所示,其中木杆AB=2 m,它
的影子BC=1.6 m,木杆PQ的影子有一部分落在了墙上,PM=1.2 m,MN
=0.8 m,则木杆PQ的长度为 m.
2.3
类型一
1
2
3
4
5
6
下一栏目
4.如图所示为某种型号的台灯的横截面图,已知台灯灯柱AB长为30 cm,且
与水平桌面垂直,灯臂AC长为10 cm,灯头的横截面△CEF为直角三角形,
当灯臂AC与灯柱AB垂直时,沿CE边射出的光线刚好射到底座点B处.若
不考虑其他因素,则该台灯在桌面上可照亮的宽度BD的长为 cm.
100
类型一
1
2
3
4
5
6
下一栏目
5.如图,小明要测量操场旗杆高度AH,立两根高1米的标杆BC和DE,两标杆
相距BD=15米,点D,B,H在一条直线上,小明从BC退行2米到点F处,
着地观察A,C,F三点共线;从DE退行3米步到G,着地观察,A,E,G三
点也共线.则旗杆的高度AH为 米,HB的长度为 米.
16
30
类型一
1
2
3
4
5
6
下一栏目
6.如图1是一把落地遮阳伞,伞柄CD垂直于水平地面GQ,当点P与点A重合
时,伞收紧;当点P由点A向点B移动时,伞慢慢撑开;当点P与点B重合时,
伞完全张开.已知遮阳伞的高度CD=220 cm,在它撑开的过程中,总有
PM=PN=CM=CN=50 cm,CE=CF=120 cm,BC=20 cm. (1)当∠CPN=53°时,求BP的长;
解:连接MN,交CD于点H. ∵CM=MP=NC=NP=50 cm,∴四边形PMCN是菱形, ∴CP⊥MN,CH=PH, ∴PH=PN·cos53°≈30(cm),PC=2PH=60 cm, ∴PB=PC-BC=40 cm.
类型一
1
2
3
4
5
6
下一栏目
(2)如图2,当伞完全张开时,求点E到地面GQ的距离.(参考数据:sin53°≈0.8,
cos53°≈0.6,tan53°≈1.3)
连接MN交CD于点J,连接EF交CD于点H. ∵四边形CMBN是菱形,∴CJ=JB=10 cm. ∵MJ∥EH,∴△CMJ∽△CEH, ∴ = ,即 = , ∴CH=24 cm, ∴HD=CD-CH=220-24=196(cm), 即当伞完全张开时,点E到地面GQ的距离为196 cm.
类型一
1
2
3
4
5
6
下一栏目
类型二 解直角三角形的实际应用 7.如图,活动课上小明利用一个锐角是30°的三角板测量一棵树的高度,已
知他与树之间的水平距离BE=9 m,AB=1.5 m(即小明的眼睛距地面的距
离),那么这棵树高是( ) A.3 m B.27 m C.(3 +1.5) m D.(27 +1.5)m
C
上一栏目
类型二
7
8
9
10
11
8.如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为30°,测得底部C
的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为60 m,那么该
建筑物的高度BC为( ) A.80 m B.60 m C.80 m D.60 m
C
上一栏目
类型二
7
8
9
10
11
9.如图,一个直角梯形的堤坝坡长AB为6米,斜坡AB的坡角为60°,为了
改善堤坝的稳固性,准备将其坡角改为45°,则调整后的斜坡AE的长度
为( ) A.3 米 B.3 米 C.(3 -2)米 D.(3 -3)米
A
上一栏目
类型二
7
8
9
10
11
10.如图,一艘海上巡逻船在A地巡航,这时接到B地海上指挥中心紧急通知:
在指挥中心北偏西60°方向的C地,有一艘渔船遇险,要求马上前去救
援.此时C地位于A北偏西30°方向上,A地位于B地北偏西75°方向上,
A,B两地之间的距离为12海里.求A,C两地之间的距离.(参考数据:
≈1.41, ≈1.73, ≈2.45,结果精确到0.1海里)
上一栏目
类型二
7
8
9
10
11
解:过点B作BD⊥CA,交CA延长线于点D. 由题意,得∠ACB=60°-30°=30°, ∠ABC=75°-60°=15°,∴∠DAB=∠DBA=45°. 在Rt△ABD中, ∵AB=12,∠DAB=45°,
∴BD=AD=ABcos45°=6 . 在Rt△CBD中,CD= =6 , ∴AC=6 -6 ≈6.2(海里). 答:A,C两地之间的距离约为6.2海里.
上一栏目
类型二
7
8
9
10
11
11.如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上
走到P处再测得点C的仰角为45°,已知OA=100米,山坡坡度(竖直高度
与水平宽度的比)i=1∶2,且点O,A,B在同一条直线上.求电视塔OC
的高度以及此人所在位置点P的铅直高度.(结果保留根号形式)
上一栏目
类型二
7
8
9
10
11
解:过点P作PE⊥OB于点E,作PF⊥CO于点F. 在Rt△AOC中, ∵AO=100米,∠CAO=60°,∴CO=AO?tan60°=100 (米). 设PE=x米, ∵tan∠PAB= = ,∴AE=2x米. 在Rt△PCF中, ∠CPF=45°,CF=(100 -x)米,PF=OA+AE=(100+2x)米. ∵PF=CF,∴100+2x=100 -x,解得x= . 答:电视塔OC高为100 米,点P的铅直高度为 米.
上一栏目
类型二
7
8
9
10
11
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
