人教版九年级下册 单元卷(八) 锐角三角函数 习题课件(37张PPT)
文档属性
| 名称 | 人教版九年级下册 单元卷(八) 锐角三角函数 习题课件(37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 20:05:46 | ||
图片预览








文档简介
单元卷(八) 锐角三角函数
测试范围:第二十八章
选择题
填空题
附加题
解答题
一、选择题(每小题3分,共30分) 1.若2sinA= ,则锐角∠A的度数为( ) A.30° B.45° C.60° D.75°
B
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
2.在△ABC中,∠C=90°,AB=6,cosA= ,则AC等于( ) A.18 B.2 C. D.
B
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
3.在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器求边
AC的长,则下列按键顺序正确的是( )
D
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
4.在Rt△ABC中,各边都扩大5倍,则∠A的三角函数值( ) A.不变 B.扩大5倍 C.缩小5倍 D.不能确定
A
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
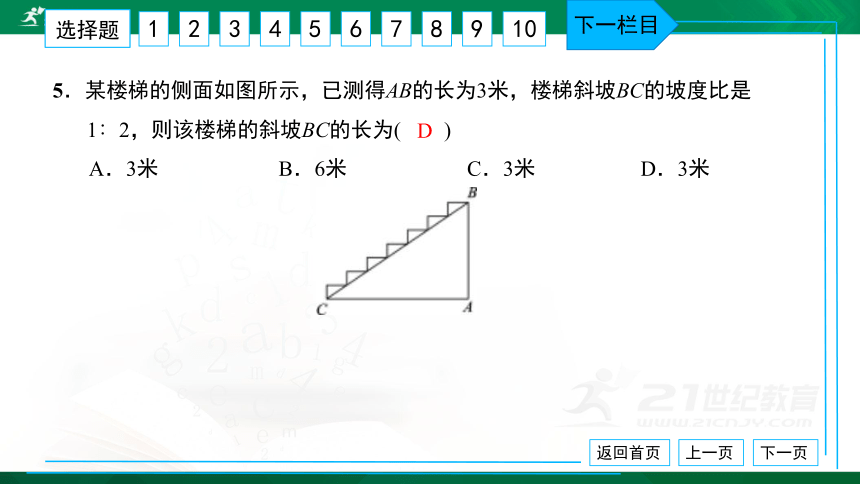
5.某楼梯的侧面如图所示,已测得AB的长为3米,楼梯斜坡BC的坡度比是
1∶2,则该楼梯的斜坡BC的长为( ) A.3米 B.6米 C.3米 D.3米
D
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
6.在△ABC中,∠A,∠B都是锐角,且sinA= ,cosB= ,则△ABC的形
状是( ) A.直角三角形 B.钝角三角形 C.锐角三角形 D.锐角三角形或钝角三角形
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
7.如图,P是∠α的边OA上一点,且点P的横坐标为3,sinα= ,则tanα=( ) A. B. C. D.
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
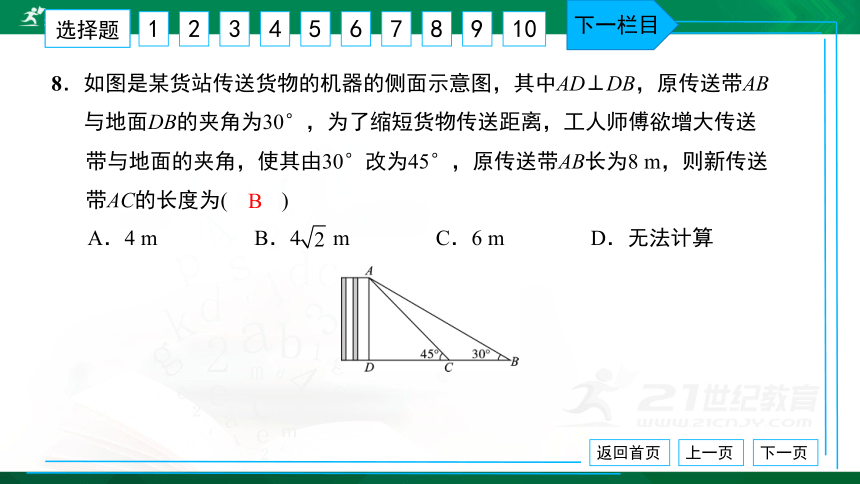
8.如图是某货站传送货物的机器的侧面示意图,其中AD⊥DB,原传送带AB
与地面DB的夹角为30°,为了缩短货物传送距离,工人师傅欲增大传送
带与地面的夹角,使其由30°改为45°,原传送带AB长为8 m,则新传送
带AC的长度为( ) A.4 m B.4 m C.6 m D.无法计算
B
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
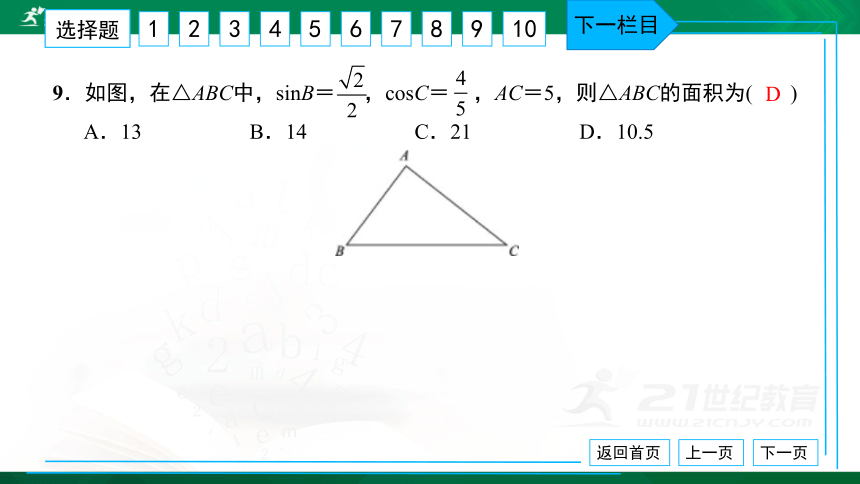
9.如图,在△ABC中,sinB= ,cosC= ,AC=5,则△ABC的面积为( ) A.13 B.14 C.21 D.10.5
D
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
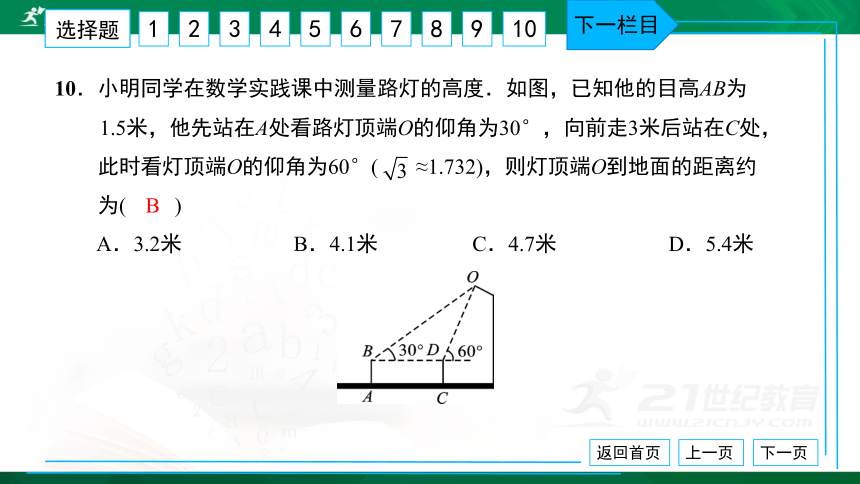
10.小明同学在数学实践课中测量路灯的高度.如图,已知他的目高AB为
1.5米,他先站在A处看路灯顶端O的仰角为30°,向前走3米后站在C处,
此时看灯顶端O的仰角为60°( ≈1.732),则灯顶端O到地面的距离约
为( ) A.3.2米 B.4.1米 C.4.7米 D.5.4米
B
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
二、填空题(每小题3分,共24分) 11.在△ABC中,∠C=90°,BC=6,tanA= ,那么AC= .
9
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
12.已知sin(α-15°)= ,则α= .
45°
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
13.如图,在正方形网格中,cos∠CAB= .
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
14.某水库堤坝的横断面如图所示,经测量知tanA= ,堤坝高BC=50 m,
则AB= m.
100
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
15.如图,一艘船以40 n mile/h的速度由西向东航行,航行到A处时,测得灯
塔P在船的北偏东30°方向上,继续航行2.5 h,到达B处,测得灯塔P在船
的北偏西60°方向上,此时船到灯塔的距离为 n mile.(结果保留根号)
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
16.如图,在四边形ABCD中,已知∠B=90°,AB=1,CD=8,AC⊥CD,
若sin∠ACB= ,则cos∠ADC= .
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
17.如图,AB为 O的直径,D为AB上一点,且AB=5AD,CD⊥AB,垂足为
D,C在圆上,设∠COD=α,则sin = .
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
18.若三角形有一边上的中线长恰好等于这边的长,则称这个三角形为“好
玩三角形”.在△ABC中,AB=AC,若△ABC是好玩三角形,则tanB=
.
2或
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
三、解答题(共66分) 19.(8分)计算: (1) +tan60°; (2)sin260°+cos245°- tan45°.
解:原式= + = .
解:原式=( )2+( )2-×1 = - .
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
20.(8分)如图,在△ABC中,∠C=90°,点D在AC上,已知∠BDC=45°,
BD=10 ,AB=20.求∠A的度数.
解:∵在Rt△BDC中, ∠BDC=45°,BD=10, ∴BC=BD?sin∠BDC=10 × =10. ∵∠C=90°,AB=20, ∴sin∠A= = = , ∴∠A=30°.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
21.(8分)如图,在△ABC中,CD⊥AB,垂足为D.若AB=12,CD=6,tanA= ,
求sinB+cosB的值.
解:在Rt△ACD中, ∵∠ADC=90°,∴tanA= = = ,
∴AD=4,∴BD=AB-AD=12-4=8. 在Rt△BCD中, ∵∠BDC=90°,BD=8,CD=6,∴BC= =10, ∴sinB= = ,cosB= = , ∴sinB+cosB= + = .
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
22.(10分)某同学用木板制作一个带有卡槽的三角形手机架,如图所示.已知AC
=20 cm,BC=18 cm,∠ACB=50°,某款手机长度为17 cm,宽为8 cm,该
同学能否将该手机放入卡槽AB内?请说明你的理由.(提示:sin50°≈0.8,
cos50°≈0.6,tan50°≈1.2)
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
解:该同学能将手机放入卡槽AB内. 理由:如下作AD⊥BC于点D. ∵∠C=50°,AC=20 cm,∴AD=AC?sin50°≈20×0.8=16 (cm), CD=AC?cos50°≈20×0.6=12 (cm). ∵BC=18 cm, ∴DB=BC-CD=18-12=6 (cm), ∴AB= = = (cm). ∵17= < , ∴该同学能将该手机放入卡槽AB内.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
23.(10分)如图,AD是△ABC的中线,tanB= ,cosC= ,AC= . (1)求BC的长;
解:过点A作AE⊥BC于点E, ∵cosC= ,∴∠C=45°. 在Rt△ACE中, ∵CE=AC?cosC=1,∴AE=CE=1. 在Rt△ABE中, ∵tanB= ,即 = , ∴BE=3AE=3,∴BC=BE+CE=4.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)求sin∠ADC的值.
∵AD是△ABC的中线, ∴CD= BC=2,∴DE=CD-CE=1. ∵AE⊥BC,DE=AE, ∴∠ADC=45°,∴sin∠ADC= .
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
24.(10分)如图1是全国最大的瓷碗造型建筑,坐落于江西景德镇,整体造型
概念来自“宋代影青斗笠碗”,造型庄重典雅,象征“万瓷之母”.小敏为
了计算该建筑物横断面(瓷碗横断面ABCD为等腰梯形)的高度,如图2,
她站在与瓷碗底部AB位于同一水平面的点P处测得瓷碗顶部点D的仰角为
45°,而后沿着一段坡度为0.44的小坡PQ步行到点Q(此过程中AD,AP,
PQ始终处于同一平面)后测得点D的仰角减少了5°.已知坡面PQ的水平距
离为20米,小敏身高忽略不计,试计算该瓷碗建筑物的高度.(参考数据:
sin40°≈0.64,tan40°≈0.84)
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
解:分别过点D,P向水平线作垂线,与过点Q的水平线分别交于点N,M,DN与PA交于点H,则四边形PMNH是矩形, ∴PM=HN,PH=MN. 由题意可知∠DPA=45°,∠DQN=45°-5°=40°. 在Rt△DHP中,∵∠DPA=45°,∴DH=PH. 设该瓷碗建筑物的高度DH为x米,则PH=DH=MN=x米.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
在Rt△PQM中,∵tan∠PQM= =0.44,QM=20米, ∴PM=0.44QM=0.44×20=8.8(米), ∴DN=DH+HN=(x+8.8)米,QN=QM+MN=(x+20)米. 在Rt△DQN中,tan∠DQN= ,∴ ≈0.84,解得x≈50. 答:该瓷碗建筑物的高度约为50米.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
25.(12分)一艘轮船向正东方向航行,在A处测得灯塔P在A的北偏东60°方向
上,航行40海里到达B处,此时测得灯塔P在B的北偏东15°方向上. (1)求灯塔P到轮船航线的距离PD是多少海里;(结果保留根号)
解:过点B作BC⊥AP于点C, ∵∠CAM=60°,∴∠BAC=30°, ∴BC= AB=20,AC=AB?cos30°=20 . ∵∠PBD=90°-15°=75°,∠ABC=90°-30°=60°, ∴∠CBP=180°-75°-60°=45°, ∴PC=BC=20,∴AP=AC+PC=20+20 . ∵PD⊥AD,∠PAD=30°,∴PD= AP=10+10 . 答:灯塔P到轮船航线的距离PD是(10+10)海里.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)当轮船从B处继续向东航行时,一艘快艇从灯塔P处同时前往D处,尽管快
艇速度是轮船速度的2倍,但快艇还是比轮船晚15分钟到达D处,求轮船每
小时航行多少海里.(结果保留到个位,参考数据: ≈1.73)
设轮船每小时航行x海里, 在Rt△ADP中,AD=AP?cos30°= ×(20+20)=30+10, ∴BD=AD-AB=30+10-40=10-10, 由题可列方程 + = ,解得x=60-20 . 经检验,x=60-20 是原方程的解,∴x=60-20≈60-20×1.73=25.4≈25. 答:轮船每小时航行25海里.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
附加题(20分) 当0°<α<60°时,下列关系式中有且仅有一个正确.
A.2sin(α+30°)=sinα+
B.2sin(α+30°)=2sinα+
C.2sin(α+30°)= sinα+cosα (1)正确的选项是 ;
C
上一栏目
附加题
(2)如图1,在△ABC中,AC=1,∠B=30°,∠A=α,请利用此图证明(1)中
的结论;
解:过点A作AD⊥BC,交BC的延长线于点D. ∵∠B=30°,∠BAC=α,AC=1,∴∠ACD=α+30°, ∴在△ADC中,AD=AC·sin∠ACD=sin(α+30°). ∵在△ABD中, ∠ADB=90°,∠B=30°, ∴AB=2AD=2sin(α+30°).
上一栏目
附加题
过点C作CE⊥AB于点E, ∴在△CEA中, CE=sinα,AE=cosα, ∴在△BEC中, EB= CE= sinα, ∴AB=AE+BE=cosα+ sinα, ∴AB=2sin(α+30°)= sinα+cosα.
上一栏目
附加题
(3)两块分别含45°角和30°角的直角三角板ABD和BCD按如图2所示的方式
放置在同一平面内,BD=8 ,求△ADC的面积.
由上面证明的等式易得sin(α+30°)= . 过点A作AG⊥CD,交CD的延长线于点G. ∵△ABD和△BCD是分别含45°角和30°角的直角
三角形,BD=8 , ∴∠ADG=75°,AD=8,CD=4 . ∵sin75°=sin(45°+30°)= = , ∴在△ADG中, AG=AD·sin∠ADG=8×sin75°=2 +2 , ∴S△ADC= CD·AG= ×4 ×(2 +2 )=8 +8.
上一栏目
附加题
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
测试范围:第二十八章
选择题
填空题
附加题
解答题
一、选择题(每小题3分,共30分) 1.若2sinA= ,则锐角∠A的度数为( ) A.30° B.45° C.60° D.75°
B
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
2.在△ABC中,∠C=90°,AB=6,cosA= ,则AC等于( ) A.18 B.2 C. D.
B
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
3.在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器求边
AC的长,则下列按键顺序正确的是( )
D
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
4.在Rt△ABC中,各边都扩大5倍,则∠A的三角函数值( ) A.不变 B.扩大5倍 C.缩小5倍 D.不能确定
A
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
5.某楼梯的侧面如图所示,已测得AB的长为3米,楼梯斜坡BC的坡度比是
1∶2,则该楼梯的斜坡BC的长为( ) A.3米 B.6米 C.3米 D.3米
D
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
6.在△ABC中,∠A,∠B都是锐角,且sinA= ,cosB= ,则△ABC的形
状是( ) A.直角三角形 B.钝角三角形 C.锐角三角形 D.锐角三角形或钝角三角形
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
7.如图,P是∠α的边OA上一点,且点P的横坐标为3,sinα= ,则tanα=( ) A. B. C. D.
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
8.如图是某货站传送货物的机器的侧面示意图,其中AD⊥DB,原传送带AB
与地面DB的夹角为30°,为了缩短货物传送距离,工人师傅欲增大传送
带与地面的夹角,使其由30°改为45°,原传送带AB长为8 m,则新传送
带AC的长度为( ) A.4 m B.4 m C.6 m D.无法计算
B
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
9.如图,在△ABC中,sinB= ,cosC= ,AC=5,则△ABC的面积为( ) A.13 B.14 C.21 D.10.5
D
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
10.小明同学在数学实践课中测量路灯的高度.如图,已知他的目高AB为
1.5米,他先站在A处看路灯顶端O的仰角为30°,向前走3米后站在C处,
此时看灯顶端O的仰角为60°( ≈1.732),则灯顶端O到地面的距离约
为( ) A.3.2米 B.4.1米 C.4.7米 D.5.4米
B
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
二、填空题(每小题3分,共24分) 11.在△ABC中,∠C=90°,BC=6,tanA= ,那么AC= .
9
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
12.已知sin(α-15°)= ,则α= .
45°
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
13.如图,在正方形网格中,cos∠CAB= .
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
14.某水库堤坝的横断面如图所示,经测量知tanA= ,堤坝高BC=50 m,
则AB= m.
100
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
15.如图,一艘船以40 n mile/h的速度由西向东航行,航行到A处时,测得灯
塔P在船的北偏东30°方向上,继续航行2.5 h,到达B处,测得灯塔P在船
的北偏西60°方向上,此时船到灯塔的距离为 n mile.(结果保留根号)
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
16.如图,在四边形ABCD中,已知∠B=90°,AB=1,CD=8,AC⊥CD,
若sin∠ACB= ,则cos∠ADC= .
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
17.如图,AB为 O的直径,D为AB上一点,且AB=5AD,CD⊥AB,垂足为
D,C在圆上,设∠COD=α,则sin = .
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
18.若三角形有一边上的中线长恰好等于这边的长,则称这个三角形为“好
玩三角形”.在△ABC中,AB=AC,若△ABC是好玩三角形,则tanB=
.
2或
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
三、解答题(共66分) 19.(8分)计算: (1) +tan60°; (2)sin260°+cos245°- tan45°.
解:原式= + = .
解:原式=( )2+( )2-×1 = - .
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
20.(8分)如图,在△ABC中,∠C=90°,点D在AC上,已知∠BDC=45°,
BD=10 ,AB=20.求∠A的度数.
解:∵在Rt△BDC中, ∠BDC=45°,BD=10, ∴BC=BD?sin∠BDC=10 × =10. ∵∠C=90°,AB=20, ∴sin∠A= = = , ∴∠A=30°.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
21.(8分)如图,在△ABC中,CD⊥AB,垂足为D.若AB=12,CD=6,tanA= ,
求sinB+cosB的值.
解:在Rt△ACD中, ∵∠ADC=90°,∴tanA= = = ,
∴AD=4,∴BD=AB-AD=12-4=8. 在Rt△BCD中, ∵∠BDC=90°,BD=8,CD=6,∴BC= =10, ∴sinB= = ,cosB= = , ∴sinB+cosB= + = .
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
22.(10分)某同学用木板制作一个带有卡槽的三角形手机架,如图所示.已知AC
=20 cm,BC=18 cm,∠ACB=50°,某款手机长度为17 cm,宽为8 cm,该
同学能否将该手机放入卡槽AB内?请说明你的理由.(提示:sin50°≈0.8,
cos50°≈0.6,tan50°≈1.2)
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
解:该同学能将手机放入卡槽AB内. 理由:如下作AD⊥BC于点D. ∵∠C=50°,AC=20 cm,∴AD=AC?sin50°≈20×0.8=16 (cm), CD=AC?cos50°≈20×0.6=12 (cm). ∵BC=18 cm, ∴DB=BC-CD=18-12=6 (cm), ∴AB= = = (cm). ∵17= < , ∴该同学能将该手机放入卡槽AB内.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
23.(10分)如图,AD是△ABC的中线,tanB= ,cosC= ,AC= . (1)求BC的长;
解:过点A作AE⊥BC于点E, ∵cosC= ,∴∠C=45°. 在Rt△ACE中, ∵CE=AC?cosC=1,∴AE=CE=1. 在Rt△ABE中, ∵tanB= ,即 = , ∴BE=3AE=3,∴BC=BE+CE=4.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)求sin∠ADC的值.
∵AD是△ABC的中线, ∴CD= BC=2,∴DE=CD-CE=1. ∵AE⊥BC,DE=AE, ∴∠ADC=45°,∴sin∠ADC= .
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
24.(10分)如图1是全国最大的瓷碗造型建筑,坐落于江西景德镇,整体造型
概念来自“宋代影青斗笠碗”,造型庄重典雅,象征“万瓷之母”.小敏为
了计算该建筑物横断面(瓷碗横断面ABCD为等腰梯形)的高度,如图2,
她站在与瓷碗底部AB位于同一水平面的点P处测得瓷碗顶部点D的仰角为
45°,而后沿着一段坡度为0.44的小坡PQ步行到点Q(此过程中AD,AP,
PQ始终处于同一平面)后测得点D的仰角减少了5°.已知坡面PQ的水平距
离为20米,小敏身高忽略不计,试计算该瓷碗建筑物的高度.(参考数据:
sin40°≈0.64,tan40°≈0.84)
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
解:分别过点D,P向水平线作垂线,与过点Q的水平线分别交于点N,M,DN与PA交于点H,则四边形PMNH是矩形, ∴PM=HN,PH=MN. 由题意可知∠DPA=45°,∠DQN=45°-5°=40°. 在Rt△DHP中,∵∠DPA=45°,∴DH=PH. 设该瓷碗建筑物的高度DH为x米,则PH=DH=MN=x米.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
在Rt△PQM中,∵tan∠PQM= =0.44,QM=20米, ∴PM=0.44QM=0.44×20=8.8(米), ∴DN=DH+HN=(x+8.8)米,QN=QM+MN=(x+20)米. 在Rt△DQN中,tan∠DQN= ,∴ ≈0.84,解得x≈50. 答:该瓷碗建筑物的高度约为50米.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
25.(12分)一艘轮船向正东方向航行,在A处测得灯塔P在A的北偏东60°方向
上,航行40海里到达B处,此时测得灯塔P在B的北偏东15°方向上. (1)求灯塔P到轮船航线的距离PD是多少海里;(结果保留根号)
解:过点B作BC⊥AP于点C, ∵∠CAM=60°,∴∠BAC=30°, ∴BC= AB=20,AC=AB?cos30°=20 . ∵∠PBD=90°-15°=75°,∠ABC=90°-30°=60°, ∴∠CBP=180°-75°-60°=45°, ∴PC=BC=20,∴AP=AC+PC=20+20 . ∵PD⊥AD,∠PAD=30°,∴PD= AP=10+10 . 答:灯塔P到轮船航线的距离PD是(10+10)海里.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)当轮船从B处继续向东航行时,一艘快艇从灯塔P处同时前往D处,尽管快
艇速度是轮船速度的2倍,但快艇还是比轮船晚15分钟到达D处,求轮船每
小时航行多少海里.(结果保留到个位,参考数据: ≈1.73)
设轮船每小时航行x海里, 在Rt△ADP中,AD=AP?cos30°= ×(20+20)=30+10, ∴BD=AD-AB=30+10-40=10-10, 由题可列方程 + = ,解得x=60-20 . 经检验,x=60-20 是原方程的解,∴x=60-20≈60-20×1.73=25.4≈25. 答:轮船每小时航行25海里.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
附加题(20分) 当0°<α<60°时,下列关系式中有且仅有一个正确.
A.2sin(α+30°)=sinα+
B.2sin(α+30°)=2sinα+
C.2sin(α+30°)= sinα+cosα (1)正确的选项是 ;
C
上一栏目
附加题
(2)如图1,在△ABC中,AC=1,∠B=30°,∠A=α,请利用此图证明(1)中
的结论;
解:过点A作AD⊥BC,交BC的延长线于点D. ∵∠B=30°,∠BAC=α,AC=1,∴∠ACD=α+30°, ∴在△ADC中,AD=AC·sin∠ACD=sin(α+30°). ∵在△ABD中, ∠ADB=90°,∠B=30°, ∴AB=2AD=2sin(α+30°).
上一栏目
附加题
过点C作CE⊥AB于点E, ∴在△CEA中, CE=sinα,AE=cosα, ∴在△BEC中, EB= CE= sinα, ∴AB=AE+BE=cosα+ sinα, ∴AB=2sin(α+30°)= sinα+cosα.
上一栏目
附加题
(3)两块分别含45°角和30°角的直角三角板ABD和BCD按如图2所示的方式
放置在同一平面内,BD=8 ,求△ADC的面积.
由上面证明的等式易得sin(α+30°)= . 过点A作AG⊥CD,交CD的延长线于点G. ∵△ABD和△BCD是分别含45°角和30°角的直角
三角形,BD=8 , ∴∠ADG=75°,AD=8,CD=4 . ∵sin75°=sin(45°+30°)= = , ∴在△ADG中, AG=AD·sin∠ADG=8×sin75°=2 +2 , ∴S△ADC= CD·AG= ×4 ×(2 +2 )=8 +8.
上一栏目
附加题
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
