人教版九年级 单元卷(二) 二次函数 习题课件(共39张PPT)
文档属性
| 名称 | 人教版九年级 单元卷(二) 二次函数 习题课件(共39张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 18:36:56 | ||
图片预览








文档简介
单元卷(二) 二次函数
测试范围:第二十二章
选择题
填空题
附加题
解答题
一、选择题(每小题3分,共30分) 1.二次函数y= x2-1的图象的顶点坐标为( ) A.(0,0) B.(0,-1) C.( ,1) D.(- ,1)
B
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
2.已知点A(-1,y1),点B(-2,y2)在抛物线y=-3x2+2上,则y1,y2的大
小关系是( ) A.y1>y2 B.y1<y2 C.y1=y2 D.无法判断
A
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
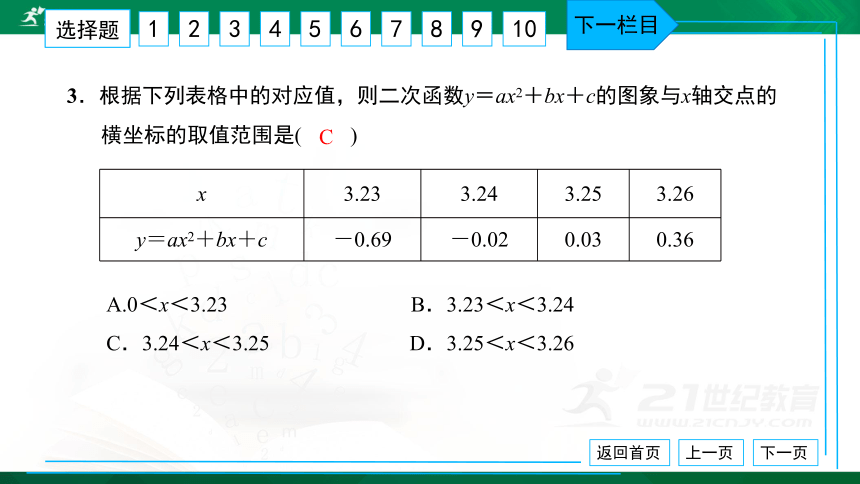
3.根据下列表格中的对应值,则二次函数y=ax2+bx+c的图象与x轴交点的
横坐标的取值范围是( )
{5940675A-B579-460E-94D1-54222C63F5DA}x
3.23
3.24
3.25
3.26
y=ax2+bx+c
-0.69
-0.02
0.03
0.36
A.0<x<3.23 B.3.23<x<3.24
C.3.24<x<3.25 D.3.25<x<3.26
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
4.抛物线y=x2-5x+6与x轴的交点情况是( ) A.有两个交点 B.只有一个交点
C.没有交点 D.无法判断
A
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
5.二次函数y=ax2+bx+c的图象如图所示,则关于x的不等式ax2+bx+c<
0的解集是( ) A.x<-1 B.x<2 C.x<-1或x>2 D.-1<x<2
D
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
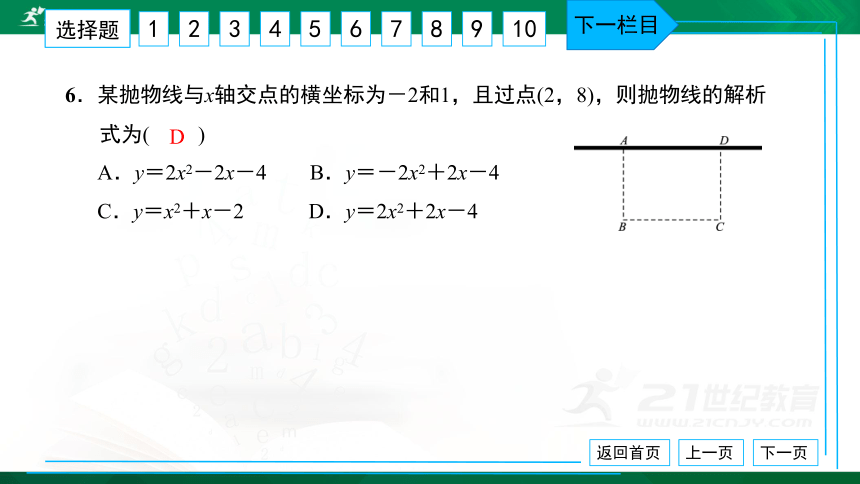
6.某抛物线与x轴交点的横坐标为-2和1,且过点(2,8),则抛物线的解析
式为( ) A.y=2x2-2x-4 B.y=-2x2+2x-4 C.y=x2+x-2 D.y=2x2+2x-4
D
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
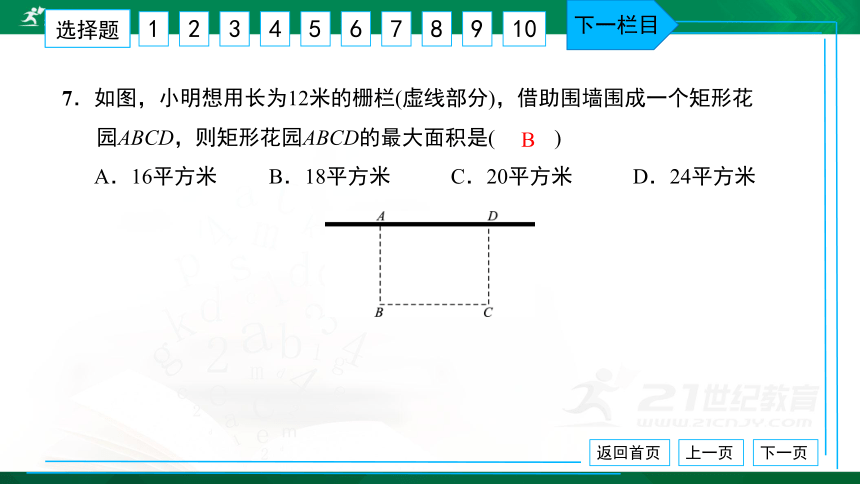
7.如图,小明想用长为12米的栅栏(虚线部分),借助围墙围成一个矩形花
园ABCD,则矩形花园ABCD的最大面积是( ) A.16平方米 B.18平方米 C.20平方米 D.24平方米
B
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
8.如图是一个抛物线形拱桥,当拱顶离水面2 m时,水面宽4 m,若水面上
升1 m,则水面宽为( ) A. m B.2 m C.2 m D.2 m
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
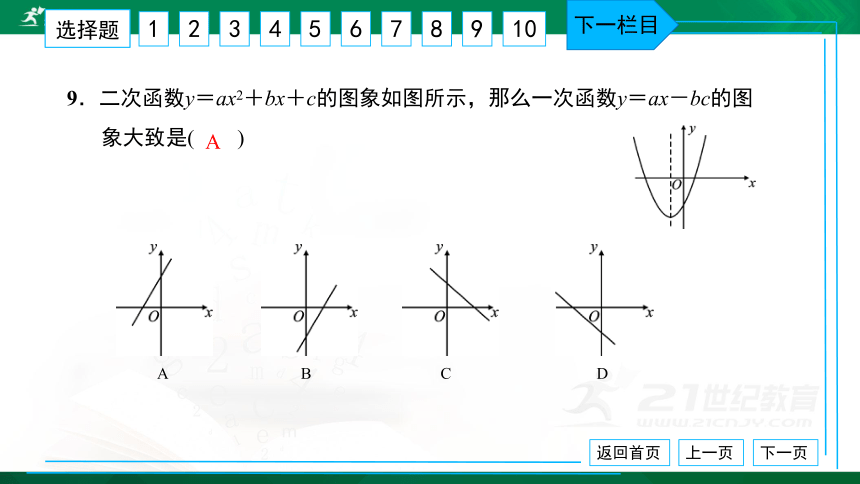
9.二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=ax-bc的图
象大致是( )
A B C D
A
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
10.二次函数y=ax2+bx+c中x与y的部分对应值如下表所示.
{5940675A-B579-460E-94D1-54222C63F5DA}x
…
-1
0
1
3
…
y
…
-1
3
5
3
…
下列结论:①ac<0;②当x>1时,y的值随x值的增大而减小;③3是方程ax2+(b-1)x+c=0的一个根;④当-1<x<3时,ax2+(b-1)x+c>0.其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
解析:描点画出二次函数的图象,可知a<0,c=3,∴ac<0,故①正确;由表格中的数据可知抛物线的对称轴是直线x= ,∴当x> 时,y的值随x值的增大而减小,故②错误;∵当x=3时,y=3,∴9a+3b+c=3,∴9a+3(b-1)+c=0,∴x=3是方程ax2+(b-1)x+c=0的一个根,故③正确;∵当x=-1时,y=-1,∴a-b+c=-1,∴a-(b-1)+c=0,∴x=-1是方程ax2+(b-1)x+c=0的一个根,∴当-1<x<3时,ax2+(b-1)x+c>0,故④正确.故选C.
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
二、填空题(每小题3分,共24分) 11.已知函数y=2xm-1+3的图象是一条抛物线,则m= .
3
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
12.已知一个二次函数的图象开口向上,顶点坐标为(2,-1),那么这个二次函数的解析式可以是 .(只需写一个)
y=2(x-2)2-1(答案不唯一)
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
13.将抛物线y=(x-1)2+2向下平移3个单位长度后,得到的抛物线所对应
的函数解析式为 .
y=(x-1)2-1或y=x2-2x
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
14.若被击打的小球飞行高度h(单位:m)与飞行时间t(单位:s)之间具有的
关系为h=20t-5t2,则小球从飞出到落地所用的时间为 s.
4
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
15.二次函数y=x2-2x+c的图象与x轴交于点A(-2,0),则图象与x轴的另
一个交点B的坐标为 .
(4,0)
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
16.当-1≤x≤3时,二次函数y=x2-4x+3的最小值为a,最大值为b,则
a+b= .
7
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
17.某旅行社有100张床位,每张床位每晚收费10元时,客床可全部租出.
若每张床每晚收费提高2元,则减少10张床位的租出;若每张床每晚收
费再提高2元,则再减少10张床位的租出…以每次提高2元的这种方法变
化下去.为了投资少而获利大,每张床每晚应提高 元.
6
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
18.抛物线y= (x-m)2与y轴交于点E,与直线l:y= x+3交于两
点,其中一个交点为F,当线段EF∥x轴时,抛物线的解析式为
.
y= (x-3 )2或y= (x+ )2
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
三、解答题(共66分) 19.(8分)已知二次函数y=- (x+4)2,将此函数的图象向右平移3个单位长
度,再向上平移2个单位长度. (1)请写出平移后图象所对应的函数解析式; (2)在如图所示的平面直角坐标系中,画出平移后的图象.
解:(1)抛物线y=- (x+4)2的顶点坐标是(-4,0),此函数的图象向右平移3个单位长度,再向上平移2个单位长度后的顶点坐标是(-1,2), 则平移后抛物线的解析式为y=- (x+1)2+2. (2)平移后的抛物线如图所示.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
20.(8分)已知抛物线y=-x2+2x+2. (1)写出该抛物线的对称轴; (2)若抛物线上两点A(x1,y1),B(x2,y2)的横坐标满足x1>x2>1,试比较y1
与y2的大小.
解:(1)∵y=-x2+2x+2=-(x-1)2+3, ∴抛物线y=-x2+2x+2的对称轴为直线x=1.
(2)∵抛物线y=-x2+2x+2 的对称轴为直线x=1,图象开口向下, ∴当x>1时,抛物线y=-x2+2x+2的y值随着x的值增大而减小, ∴当x1>x2>1时,y1<y2.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
21.(8分)已知抛物线y=x2+bx+c与x轴只有一个交点,且交点为A(-2,0). (1)求b,c的值; (2)若抛物线与y轴的交点为B,坐标原点为O,求△OAB的面积.
解:(1)∵抛物线y=x2+bx+c与x轴只有一个交点,且交点为A(-2,0), ∴抛物线的解析式为y=(x+2)2,即y=x2+4x+4, ∴b=4,c=4.
(2)∵点A的坐标为(-2,0), ∴OA=2.当x=0时,y=x2+4x+4=4, ∴点B的坐标为(0,4),∴OB=4, ∴S△OAB= OA·OB= ×2×4=4.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
22.(10分)文具店某种文具进价为每件20元.市场调查反映:当售价为每件30
元时,平均每星期可售出140件;而当每件的售价涨1元时,平均每星期
少售出10件.设每件涨价x元,平均每星期的利润为y元. (1)求出y与x的函数关系式,并写出自变量的取值范围;
解:(1)y=(30+x-20)(140-10x)=-10x2+40x+1400(0≤x≤14).
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)如何定价才能使每星期的利润最大?每星期的最大利润是多少?
解:(2)∵y=-10x2+40x+1400=-10(x-2)2+1440, ∴顶点坐标为(2,1440). ∵-10<0, ∴当x=2时,y有最大值,最大值为1440.此时定价为30+2=32(元). 答:定价为32元时,每星期的利润最大,最大利润为1440元.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
23.(10分)如图,二次函数y=(x+2)2+m的图象与y轴交于点C,点B在抛物
线上,且与点C关于抛物线的对称轴对称,已知一次函数y=kx+b的图象
经过该二次函数图象上的点A(-1,0)及点B.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(1)求二次函数与一次函数的解析式;
解:(1)∵抛物线y=(x+2)2+m经过点A(-1,0),∴1+m=0,解得m=-1, ∴抛物线的解析式为y=(x+2)2-1=x2+4x+3, ∴点C的坐标为(0,3). ∵对称轴为直线x=-2,B,C两点关于对称轴对称, ∴点B的坐标为(-4,3). ∵y=kx+b经过点A(-1,0),B(-4,3), ∴ 解得
∴一次函数的解析式为y=-x-1.
k=-1,
b=-1,
-k+b=0,
-4k+b=3,
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)根据图象,写出满足(x+2)2+m≥kx+b的x的取值范围.
(2)由图象可知,满足(x+2)2+m≥kx+b的x的取值范围为x≤-4或x≥-1.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
24.(10分)甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部
分,如图,甲在点O正上方1 m的P处发出一球,羽毛球飞行的高度y(m)
与水平距离x(m)之间满足函数解析式y=a(x-4)2+h.已知点O与球网的水
平距离为5 m,球网的高度为1.55 m.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(1)当a=- 时,①求h的值;②通过计算判断此球能否过网;
解:(1)①当a=- 时,y=- (x-4)2+h,将点P(0,1)代入,得- ×16+h=1,解得h= . ②由①可知h= , ∴y=- (x-4)2+ ,把x=5代入,得y=
- ×(5-4)2+ =1.625. ∵1.625>1.55,∴此球能过网.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7 m,离地面的高度为
m的Q处时,乙扣球成功,求a的值.
解:把(0,1),(7, )代入y=a(x-4)2+h,得
两式相减,得16a-9a=- ,解得a=- .
16a+h=1,
9a+h= ,
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
25.(12分)如图,抛物线y=x2-3x+ 与x轴相交于A,B两点,与y轴相交于
点C,D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC
相交于点E. (1)求直线BC的解析式;
解:(1)令y=0,则x2-3x+ =0,解得x= 或 , ∴点A的坐标为( ,0),点B的坐标( ,0). 令x=0,则y= ,∴点C的坐标为(0, ). 设直线BC的解析式为y=kx+b, 则 解得 ∴直线BC的解析式为y=- x+ .
k+b=0,
b= ,
k=- ,
b= ,
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)当线段DE的长度最大时,求点D的坐标.
解:设点D的坐标为(m,m2-3m+ ),则点E的坐标为(m,- m+ ) .设DE的长度为d. ∵点D是直线BC下方抛物线上一点, 则d=- m+ -(m,m2-3m+ )=-m2+ m. ∵a=-1<0,∴当m=- = 时,d取最大值, 即线段DE的长度最大,此时m2-3m+ =- , ∴点D的坐标为( ,- ).
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
附加题(20分) 已知M为二次函数y=-(x-b)2+4b+1图象的顶点,直线y=mx+5分别交x轴正半轴、y轴于点A,B. (1)如图1,若二次函数图象也经过点A,B,试求该二次函数的解析式,并求m
的值;
上一栏目
附加题
解:(1)在y=mx+5中, 当x=0时,y=5, ∴点B的坐标为B(0,5). 把点B(0,5)代入二次函数解析式,得-b2+4b+1=5,解得b=2, ∴二次函数的解析式为y=-(x-2)2+9. 当y=0时,即-(x-2)2+9=0,解得x1=5,x2=-1. ∵点A在x轴的正半轴上, ∴点A的坐标为(5,0). 把点A(5,0)代入y=mx+5,得m=-1.
上一栏目
附加题
(2)如图2,点A的坐标为(5,0),点M在△AOB内,若点C( ,y1),D( ,y2)
都在二次函数的图象上,试比较y1与y2的大小.
解:∵点A(5,0)在直线y=mx+5上, ∴5m+5=0,解得m=-1, ∴直线AB的解析式为y=-x+5,∴点B的坐标为(0,5). ∵二次函数y=-(x-b)2+4b+1, ∴顶点M的坐标为(b,4b+1). ∵点M在△AOB内部, ∴ 解得0<b< .
00<4b+1<5,
-b+5>4b+1,
上一栏目
附加题
由抛物线的对称轴为直线x=b,分三种情况讨论: ①当0<b< 时,点C( ,y1),D( ,y2)根据抛物线的对称性和增减性可得y1>y2; ②当b= 时,点C( ,y1),D( ,y2)根据抛物线的对称性和增减性可得y1=y2; ③当 <b< 时,点C( ,y1),D( ,y2)根据抛物线的对称性和增减性可得y1<y2. 综上所述,当0<b< 时,y1>y2; 当b= 时,y1=y2; 当 <b< 时,y1<y2.
上一栏目
附加题
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
测试范围:第二十二章
选择题
填空题
附加题
解答题
一、选择题(每小题3分,共30分) 1.二次函数y= x2-1的图象的顶点坐标为( ) A.(0,0) B.(0,-1) C.( ,1) D.(- ,1)
B
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
2.已知点A(-1,y1),点B(-2,y2)在抛物线y=-3x2+2上,则y1,y2的大
小关系是( ) A.y1>y2 B.y1<y2 C.y1=y2 D.无法判断
A
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
3.根据下列表格中的对应值,则二次函数y=ax2+bx+c的图象与x轴交点的
横坐标的取值范围是( )
{5940675A-B579-460E-94D1-54222C63F5DA}x
3.23
3.24
3.25
3.26
y=ax2+bx+c
-0.69
-0.02
0.03
0.36
A.0<x<3.23 B.3.23<x<3.24
C.3.24<x<3.25 D.3.25<x<3.26
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
4.抛物线y=x2-5x+6与x轴的交点情况是( ) A.有两个交点 B.只有一个交点
C.没有交点 D.无法判断
A
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
5.二次函数y=ax2+bx+c的图象如图所示,则关于x的不等式ax2+bx+c<
0的解集是( ) A.x<-1 B.x<2 C.x<-1或x>2 D.-1<x<2
D
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
6.某抛物线与x轴交点的横坐标为-2和1,且过点(2,8),则抛物线的解析
式为( ) A.y=2x2-2x-4 B.y=-2x2+2x-4 C.y=x2+x-2 D.y=2x2+2x-4
D
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
7.如图,小明想用长为12米的栅栏(虚线部分),借助围墙围成一个矩形花
园ABCD,则矩形花园ABCD的最大面积是( ) A.16平方米 B.18平方米 C.20平方米 D.24平方米
B
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
8.如图是一个抛物线形拱桥,当拱顶离水面2 m时,水面宽4 m,若水面上
升1 m,则水面宽为( ) A. m B.2 m C.2 m D.2 m
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
9.二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=ax-bc的图
象大致是( )
A B C D
A
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
10.二次函数y=ax2+bx+c中x与y的部分对应值如下表所示.
{5940675A-B579-460E-94D1-54222C63F5DA}x
…
-1
0
1
3
…
y
…
-1
3
5
3
…
下列结论:①ac<0;②当x>1时,y的值随x值的增大而减小;③3是方程ax2+(b-1)x+c=0的一个根;④当-1<x<3时,ax2+(b-1)x+c>0.其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
解析:描点画出二次函数的图象,可知a<0,c=3,∴ac<0,故①正确;由表格中的数据可知抛物线的对称轴是直线x= ,∴当x> 时,y的值随x值的增大而减小,故②错误;∵当x=3时,y=3,∴9a+3b+c=3,∴9a+3(b-1)+c=0,∴x=3是方程ax2+(b-1)x+c=0的一个根,故③正确;∵当x=-1时,y=-1,∴a-b+c=-1,∴a-(b-1)+c=0,∴x=-1是方程ax2+(b-1)x+c=0的一个根,∴当-1<x<3时,ax2+(b-1)x+c>0,故④正确.故选C.
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
二、填空题(每小题3分,共24分) 11.已知函数y=2xm-1+3的图象是一条抛物线,则m= .
3
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
12.已知一个二次函数的图象开口向上,顶点坐标为(2,-1),那么这个二次函数的解析式可以是 .(只需写一个)
y=2(x-2)2-1(答案不唯一)
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
13.将抛物线y=(x-1)2+2向下平移3个单位长度后,得到的抛物线所对应
的函数解析式为 .
y=(x-1)2-1或y=x2-2x
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
14.若被击打的小球飞行高度h(单位:m)与飞行时间t(单位:s)之间具有的
关系为h=20t-5t2,则小球从飞出到落地所用的时间为 s.
4
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
15.二次函数y=x2-2x+c的图象与x轴交于点A(-2,0),则图象与x轴的另
一个交点B的坐标为 .
(4,0)
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
16.当-1≤x≤3时,二次函数y=x2-4x+3的最小值为a,最大值为b,则
a+b= .
7
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
17.某旅行社有100张床位,每张床位每晚收费10元时,客床可全部租出.
若每张床每晚收费提高2元,则减少10张床位的租出;若每张床每晚收
费再提高2元,则再减少10张床位的租出…以每次提高2元的这种方法变
化下去.为了投资少而获利大,每张床每晚应提高 元.
6
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
18.抛物线y= (x-m)2与y轴交于点E,与直线l:y= x+3交于两
点,其中一个交点为F,当线段EF∥x轴时,抛物线的解析式为
.
y= (x-3 )2或y= (x+ )2
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
三、解答题(共66分) 19.(8分)已知二次函数y=- (x+4)2,将此函数的图象向右平移3个单位长
度,再向上平移2个单位长度. (1)请写出平移后图象所对应的函数解析式; (2)在如图所示的平面直角坐标系中,画出平移后的图象.
解:(1)抛物线y=- (x+4)2的顶点坐标是(-4,0),此函数的图象向右平移3个单位长度,再向上平移2个单位长度后的顶点坐标是(-1,2), 则平移后抛物线的解析式为y=- (x+1)2+2. (2)平移后的抛物线如图所示.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
20.(8分)已知抛物线y=-x2+2x+2. (1)写出该抛物线的对称轴; (2)若抛物线上两点A(x1,y1),B(x2,y2)的横坐标满足x1>x2>1,试比较y1
与y2的大小.
解:(1)∵y=-x2+2x+2=-(x-1)2+3, ∴抛物线y=-x2+2x+2的对称轴为直线x=1.
(2)∵抛物线y=-x2+2x+2 的对称轴为直线x=1,图象开口向下, ∴当x>1时,抛物线y=-x2+2x+2的y值随着x的值增大而减小, ∴当x1>x2>1时,y1<y2.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
21.(8分)已知抛物线y=x2+bx+c与x轴只有一个交点,且交点为A(-2,0). (1)求b,c的值; (2)若抛物线与y轴的交点为B,坐标原点为O,求△OAB的面积.
解:(1)∵抛物线y=x2+bx+c与x轴只有一个交点,且交点为A(-2,0), ∴抛物线的解析式为y=(x+2)2,即y=x2+4x+4, ∴b=4,c=4.
(2)∵点A的坐标为(-2,0), ∴OA=2.当x=0时,y=x2+4x+4=4, ∴点B的坐标为(0,4),∴OB=4, ∴S△OAB= OA·OB= ×2×4=4.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
22.(10分)文具店某种文具进价为每件20元.市场调查反映:当售价为每件30
元时,平均每星期可售出140件;而当每件的售价涨1元时,平均每星期
少售出10件.设每件涨价x元,平均每星期的利润为y元. (1)求出y与x的函数关系式,并写出自变量的取值范围;
解:(1)y=(30+x-20)(140-10x)=-10x2+40x+1400(0≤x≤14).
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)如何定价才能使每星期的利润最大?每星期的最大利润是多少?
解:(2)∵y=-10x2+40x+1400=-10(x-2)2+1440, ∴顶点坐标为(2,1440). ∵-10<0, ∴当x=2时,y有最大值,最大值为1440.此时定价为30+2=32(元). 答:定价为32元时,每星期的利润最大,最大利润为1440元.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
23.(10分)如图,二次函数y=(x+2)2+m的图象与y轴交于点C,点B在抛物
线上,且与点C关于抛物线的对称轴对称,已知一次函数y=kx+b的图象
经过该二次函数图象上的点A(-1,0)及点B.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(1)求二次函数与一次函数的解析式;
解:(1)∵抛物线y=(x+2)2+m经过点A(-1,0),∴1+m=0,解得m=-1, ∴抛物线的解析式为y=(x+2)2-1=x2+4x+3, ∴点C的坐标为(0,3). ∵对称轴为直线x=-2,B,C两点关于对称轴对称, ∴点B的坐标为(-4,3). ∵y=kx+b经过点A(-1,0),B(-4,3), ∴ 解得
∴一次函数的解析式为y=-x-1.
k=-1,
b=-1,
-k+b=0,
-4k+b=3,
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)根据图象,写出满足(x+2)2+m≥kx+b的x的取值范围.
(2)由图象可知,满足(x+2)2+m≥kx+b的x的取值范围为x≤-4或x≥-1.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
24.(10分)甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部
分,如图,甲在点O正上方1 m的P处发出一球,羽毛球飞行的高度y(m)
与水平距离x(m)之间满足函数解析式y=a(x-4)2+h.已知点O与球网的水
平距离为5 m,球网的高度为1.55 m.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(1)当a=- 时,①求h的值;②通过计算判断此球能否过网;
解:(1)①当a=- 时,y=- (x-4)2+h,将点P(0,1)代入,得- ×16+h=1,解得h= . ②由①可知h= , ∴y=- (x-4)2+ ,把x=5代入,得y=
- ×(5-4)2+ =1.625. ∵1.625>1.55,∴此球能过网.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7 m,离地面的高度为
m的Q处时,乙扣球成功,求a的值.
解:把(0,1),(7, )代入y=a(x-4)2+h,得
两式相减,得16a-9a=- ,解得a=- .
16a+h=1,
9a+h= ,
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
25.(12分)如图,抛物线y=x2-3x+ 与x轴相交于A,B两点,与y轴相交于
点C,D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC
相交于点E. (1)求直线BC的解析式;
解:(1)令y=0,则x2-3x+ =0,解得x= 或 , ∴点A的坐标为( ,0),点B的坐标( ,0). 令x=0,则y= ,∴点C的坐标为(0, ). 设直线BC的解析式为y=kx+b, 则 解得 ∴直线BC的解析式为y=- x+ .
k+b=0,
b= ,
k=- ,
b= ,
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)当线段DE的长度最大时,求点D的坐标.
解:设点D的坐标为(m,m2-3m+ ),则点E的坐标为(m,- m+ ) .设DE的长度为d. ∵点D是直线BC下方抛物线上一点, 则d=- m+ -(m,m2-3m+ )=-m2+ m. ∵a=-1<0,∴当m=- = 时,d取最大值, 即线段DE的长度最大,此时m2-3m+ =- , ∴点D的坐标为( ,- ).
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
附加题(20分) 已知M为二次函数y=-(x-b)2+4b+1图象的顶点,直线y=mx+5分别交x轴正半轴、y轴于点A,B. (1)如图1,若二次函数图象也经过点A,B,试求该二次函数的解析式,并求m
的值;
上一栏目
附加题
解:(1)在y=mx+5中, 当x=0时,y=5, ∴点B的坐标为B(0,5). 把点B(0,5)代入二次函数解析式,得-b2+4b+1=5,解得b=2, ∴二次函数的解析式为y=-(x-2)2+9. 当y=0时,即-(x-2)2+9=0,解得x1=5,x2=-1. ∵点A在x轴的正半轴上, ∴点A的坐标为(5,0). 把点A(5,0)代入y=mx+5,得m=-1.
上一栏目
附加题
(2)如图2,点A的坐标为(5,0),点M在△AOB内,若点C( ,y1),D( ,y2)
都在二次函数的图象上,试比较y1与y2的大小.
解:∵点A(5,0)在直线y=mx+5上, ∴5m+5=0,解得m=-1, ∴直线AB的解析式为y=-x+5,∴点B的坐标为(0,5). ∵二次函数y=-(x-b)2+4b+1, ∴顶点M的坐标为(b,4b+1). ∵点M在△AOB内部, ∴ 解得0<b< .
0
-b+5>4b+1,
上一栏目
附加题
由抛物线的对称轴为直线x=b,分三种情况讨论: ①当0<b< 时,点C( ,y1),D( ,y2)根据抛物线的对称性和增减性可得y1>y2; ②当b= 时,点C( ,y1),D( ,y2)根据抛物线的对称性和增减性可得y1=y2; ③当 <b< 时,点C( ,y1),D( ,y2)根据抛物线的对称性和增减性可得y1<y2. 综上所述,当0<b< 时,y1>y2; 当b= 时,y1=y2; 当 <b< 时,y1<y2.
上一栏目
附加题
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
