人教版九年级 单元卷(七) 相似 习题课件(共37张PPT)
文档属性
| 名称 | 人教版九年级 单元卷(七) 相似 习题课件(共37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 17:18:43 | ||
图片预览






文档简介
单元卷(七) 相 似
测试范围:第二十七章
选择题
填空题
附加题
解答题
一、选择题(每小题3分,共30分) 1.下列四条线段是成比例线段的是( ) A.1,1,2,3 B.1,2,3,4
C.2,2,3,3 D.2,3,4,5
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
2.已知两个相似三角形的相似比为4∶9,则它们周长的比为( ) A.2∶3 B.4∶9 C.3∶2 D.16∶81
B
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
3.下列各组图形中一定是相似形的是( ) A.两个直角三角形 B.两个等边三角形 C.两个菱形 D.两个矩形
B
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
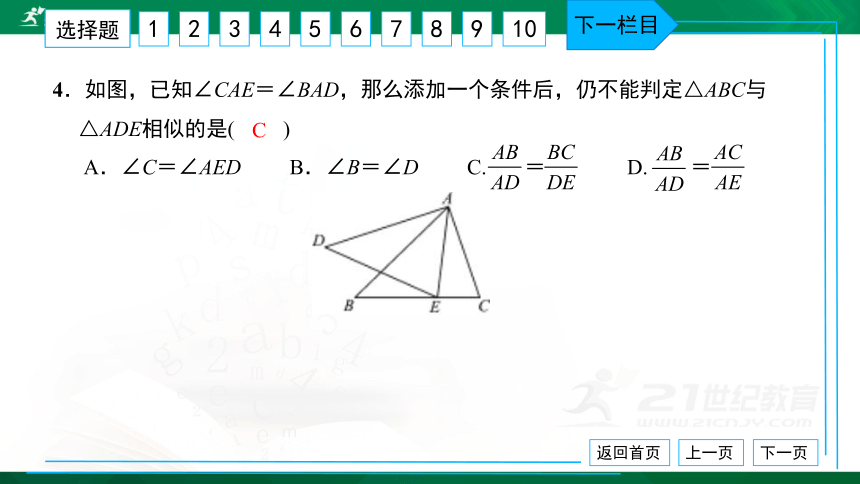
4.如图,已知∠CAE=∠BAD,那么添加一个条件后,仍不能判定△ABC与
△ADE相似的是( ) A.∠C=∠AED B.∠B=∠D C. = D. =
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
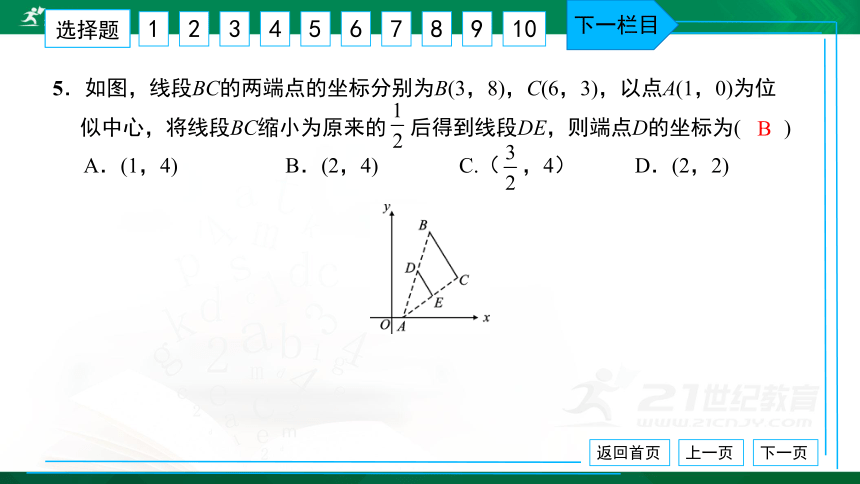
5.如图,线段BC的两端点的坐标分别为B(3,8),C(6,3),以点A(1,0)为位
似中心,将线段BC缩小为原来的 后得到线段DE,则端点D的坐标为( ) A.(1,4) B.(2,4) C.( ,4) D.(2,2)
B
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
6.如图,已知l1∥l2∥l3,AB=3,BC=2,CD=1,那么下列式子中不成立
的是( ) A.EC∶CG=5∶1 B.EF∶FG=1∶1
C.EF∶FC=3∶2 D.EF∶EG=3∶5
D
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
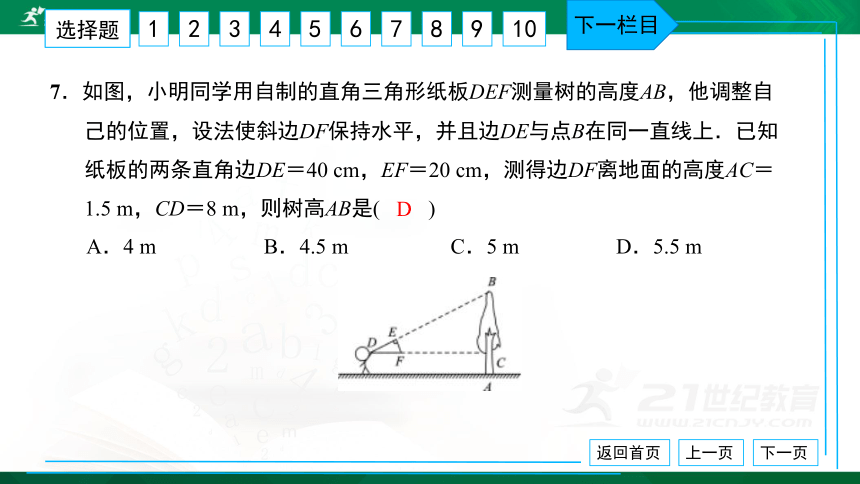
7.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自
己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知
纸板的两条直角边DE=40 cm,EF=20 cm,测得边DF离地面的高度AC=
1.5 m,CD=8 m,则树高AB是( ) A.4 m B.4.5 m C.5 m D.5.5 m
D
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
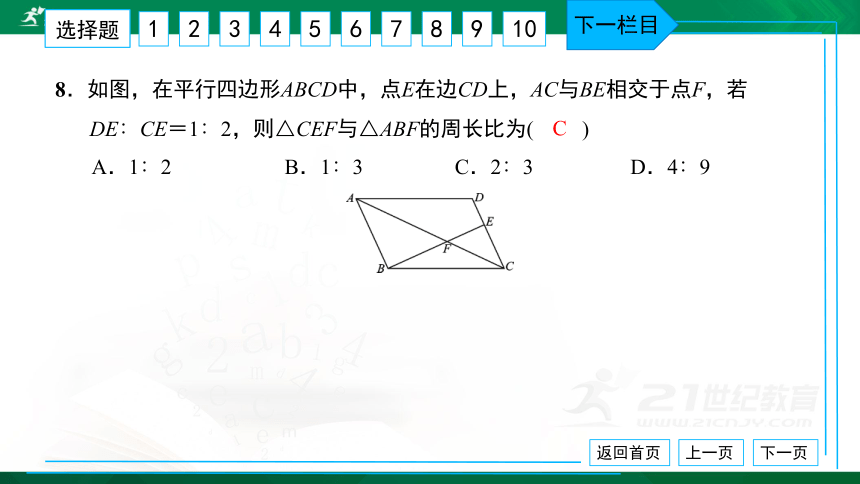
8.如图,在平行四边形ABCD中,点E在边CD上,AC与BE相交于点F,若
DE∶CE=1∶2,则△CEF与△ABF的周长比为( ) A.1∶2 B.1∶3 C.2∶3 D.4∶9
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
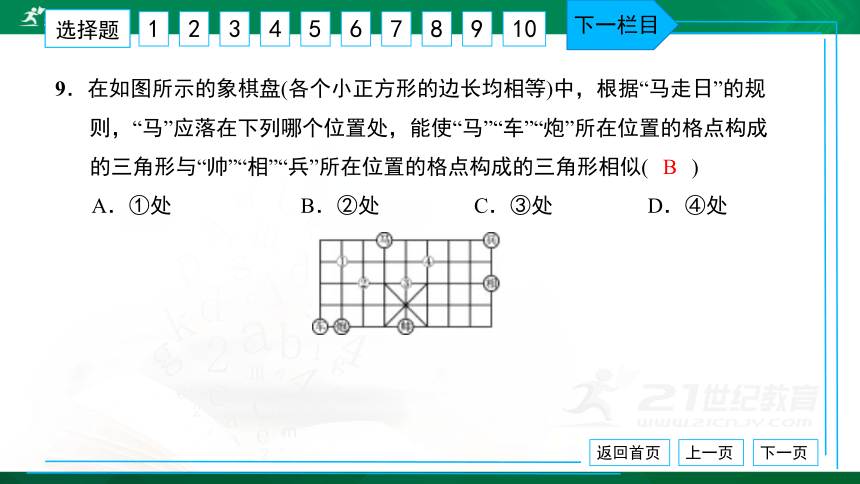
9.在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规
则,“马”应落在下列哪个位置处,能使“马”“车”“炮”所在位置的格点构成
的三角形与“帅”“相”“兵”所在位置的格点构成的三角形相似( ) A.①处 B.②处 C.③处 D.④处
B
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
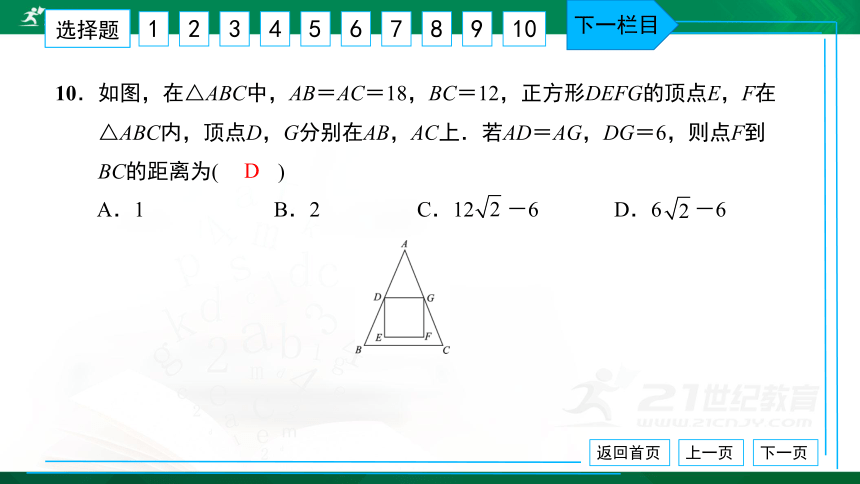
10.如图,在△ABC中,AB=AC=18,BC=12,正方形DEFG的顶点E,F在
△ABC内,顶点D,G分别在AB,AC上.若AD=AG,DG=6,则点F到
BC的距离为( ) A.1 B.2 C.12 -6 D.6 -6
D
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
二、填空题(每小题3分,共24分) 11.若 = ,则 = .
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
12.如图,四边形ABCD与四边形EFGH位似,位似中心是点O,若 = ,
则 = .
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
13.如图,在△ABC中,EF∥BC,AD⊥BC交EF于点G,EF=4,BC=5,AD
=3,则AG= .
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
14.如图是用杠杆撬石头的示意图,C是支点,当用力压杠杆的A端时,杠杆
绕点C转动,另一端B向上翘起,石头就被撬动.现有一块石头,要使其
滚动,杠杆的B端必须向上翘起10 cm.已知杠杆的动力臂AC与阻力臂BC之
比为5∶1,要使这块石头滚动,至少要将杠杆的A端向下压 cm.
50
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
15.如图,在 O中,弦AB与弦CD交于点M,且CM∶BM=3∶2,则DM∶AM
= .
2∶3
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
16.如图,在平行四边形ABCD中,E是BC边延长线上一点,AE交CD于点F,
则图中相似三角形有 对.
4
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
17.如图,已知∠ACB=∠ADC=90°,AD=2,CD= ,当AB的长为 .
时,△ACB与△ADC相似.
3或3
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
18.如图,△ABC是面积为27 cm2的等边三角形,被一平行于BC的矩形所截,
AB被截成三等份,则图中阴影部分的面积为 cm2.
9
解析: ∵矩形平行于BC,∴EH∥FG∥BC, ∴△AEH∽△AFG∽△ABC. ∵AB被截成三等份,∴AF=2AE,AB=3AE, ∴S△AEH∶S△AFG∶S△ABC=1∶4∶9, ∴S△AEH∶S四边形EFGH∶S四边形FBCG=1∶3∶5, ∴图中阴影部分的面积S四边形EFGH= ×27=9 (cm2).
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
三、解答题(共66分) 19.(8分)如图,在10×10的网格图中,△ABC三个顶点的坐标分别为A(-4,1),
B(-1,1),C(-2,4). (1)以A为位似中心,将△ABC放大为原来的2倍得到△AB1C1,请在网格图画
出△AB1C1; (2)直接写出(1)中点B1,C1的坐标.
解:(1)如图所示,△AB1C1即为所作.
(2)B1(2,1),C1(0,7).
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
20.(8分)如图,在△ABC中,AB=AC,∠EDF=∠B.求证:△BED∽△CDF.
证明:∵∠EDC=∠EDF+∠FDC=∠B+∠BED,∠EDF=∠B, ∴∠FDC=∠BED. ∵AB=AC, ∴∠B=∠C, ∴△BED∽△CDF.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
21.(8分)如图,EG∥BC,GF∥CD,AE=3,EB=2,AF=6,求AD的长.
解:∵AE=3,EB=2, ∴AB=5. ∵EG∥BC,GF∥CD, ∴ = = , = = . ∵AF=6, ∴AD=10.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
22.(10分)如图,矩形ABCD为台球桌面,AD=280 cm,AB=140 cm,球目前
在点E处,AE=35 cm,如果小丁瞄准BC边上的点F将球打过去,经过反
弹后,球刚好弹到点D处. (1)求证:△BEF∽△CDF;
证明:∵∠EFG=∠DFG, ∴∠EFB=∠DFC. 又∵∠B=∠C=90°, ∴△BEF∽△CDF.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
22.(10分)如图,矩形ABCD为台球桌面,AD=280 cm,AB=140 cm,球目前
在点E处,AE=35 cm,如果小丁瞄准BC边上的点F将球打过去,经过反
弹后,球刚好弹到点D处. (2)求CF的长.
解:∵△BEF∽△CDF, ∴ = . 设FC=x cm,则 = , 解得x=160, ∴CF的长为160 cm.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
23.(10分)如图,在正方形ABCD中,E,F分别是边AD,CD上的点,且E为
AD的中点,FC=3DF,连接EF并延长交BC的延长线于点G. (1)求证:△ABE∽△DEF;
证明:设正方形的边长为4a. ∵E为AD的中点,∴AE=ED=2a. ∵FC=3DF,∴DF=a,FC=3a, ∴ = = . ∵∠A=∠D=90°, ∴△ABE∽△DEF.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)若正方形的边长为4,求△BEG的面积.
解:∵AD=4,∴DE=2. ∵AD∥BC,∴△EDF∽△GCF, ∴ = =3,∴CG=6, ∴BG=BC+CG=10, ∴S△BEG= ×BG×AB=20.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
24.(10分)如图,小明和大伟想利用所学的几何知识测量学校操场上旗杆的高
度,他们的测量方案如下:他们两次利用镜子,第一次他把镜子放在点C
处,人在点F处正好在镜子中看见旗杆顶端A;第二次把镜子放在点D处,
人在点H处正好在镜子中看到旗杆顶端A.已知图中的所有点均在同一平面内,
AB⊥BH,GH⊥BH,EF⊥BH,小明的眼睛距离地面的距离EF=GH=1.68
米,量得CD=10米,CF=2.4米,DH=3.6米,请你利用这些数据求出旗杆
的高度.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
解:根据反射定律可以推出∠ACB=∠ECF,∠ADB=∠GDH. ∵AB⊥BC,EF⊥BC,GH⊥BC, ∴△BAC∽△FEC,△ADB∽△GDH, ∴ = , = . 设AB=x,BC=y,则 = , = ,解得x=14,y=20, 故旗杆的高度为14米.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
25.(12分)在等腰△ABC中,AB=AC=10,BC=12,D为底边BC的中点,以D
为顶点的角∠PDQ=∠B. (1)如图1,若射线DQ经过点A,DP交AC于点E,写出与△CDE相似的三角
形,并说明理由;
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
解:与△CDE相似的三角形为△ABD,△ACD,△ADE.理由如下: ∵AB=AC,D为底边BC的中点, ∴∠B=∠C,AD⊥BC, ∴∠ADB=∠ADC=90°,∴△ABD∽△ACD. ∵∠PDQ=∠B,∴∠PDQ=∠C. 又∵∠DAE=∠CAD,∴△ADE∽△ACD. ∵∠CDE+∠PDQ=90°,∴∠C+∠PDQ=90°,∴∠CED=90°=∠ADC. 又∵∠C=∠C,∴△CDE∽△CAD,∴△ABD∽△ACD∽△ADE∽△CDE.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)如图2,若射线DQ交AB于点F,DP交AC于点E,设AF=x,AE=y,求y与x的
函数关系式;(不要求写出自变量的取值范围)
∴∠EDC=∠BFD,∴△BDF∽△CED,
∴ = . ∵D为BC的中点,∴BD=CD=6,
∴ = ,∴y= .
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(3)在(2)的条件下,连接EF,则△DEF与△CDE相似吗?试说明理由.
△DEF与△CDE相似.理由如下:由(2)可知△BDF∽△CED, ∴ = . ∵BD=CD,∴ = . 又∵∠EDF=∠B=∠C,∴△DEF∽△CDE.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
附加题(20分) 如图,在△ABC中,AB=BC=10,以AB为直径作 O分别交AC,BC于点D,E,连接DE和DB,过点E作EF⊥AB,垂足为F,交BD于点F. (1)求证:AD=DE;
证明:∵AB是 O的直径, ∴∠ADB=90°. 又∵AB=BC, ∴AD=CD= AC,∠ABD=∠CBD, ∴AD=DE.
上一栏目
附加题
(2)若CE=2,求线段CD的长;
解:∵四边形ABED内接于 O, ∴∠CBA=∠CDE. 又∵∠C=∠C, ∴△CDE∽△CBA, ∴ = . ∵AB=BC=10,CE=2,CD= AC, ∴ = . ∴CD= .
上一栏目
附加题
(3)在(2)的条件下,求△DPE的面积.
解:延长EF,交 O于点M.在Rt△ABD中 , ∵AD= ,AB=10,∴BD=3 . ∵AB⊥EM,AB是直径,∴ = , ∴∠BEP=∠EDB,∴△BPE∽△BED,∴ = , 即 = ,∴BP= , ∴DP=BD-BP= , ∴S△DPE∶S△BDE=DP∶BD=13∶45. ∵S△BDC= × ×3 =15,S△BDE∶S△BDC=BE∶BC=4∶5, ∴S△BDE=12,∴S△DPE= .
上一栏目
附加题
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
测试范围:第二十七章
选择题
填空题
附加题
解答题
一、选择题(每小题3分,共30分) 1.下列四条线段是成比例线段的是( ) A.1,1,2,3 B.1,2,3,4
C.2,2,3,3 D.2,3,4,5
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
2.已知两个相似三角形的相似比为4∶9,则它们周长的比为( ) A.2∶3 B.4∶9 C.3∶2 D.16∶81
B
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
3.下列各组图形中一定是相似形的是( ) A.两个直角三角形 B.两个等边三角形 C.两个菱形 D.两个矩形
B
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
4.如图,已知∠CAE=∠BAD,那么添加一个条件后,仍不能判定△ABC与
△ADE相似的是( ) A.∠C=∠AED B.∠B=∠D C. = D. =
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
5.如图,线段BC的两端点的坐标分别为B(3,8),C(6,3),以点A(1,0)为位
似中心,将线段BC缩小为原来的 后得到线段DE,则端点D的坐标为( ) A.(1,4) B.(2,4) C.( ,4) D.(2,2)
B
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
6.如图,已知l1∥l2∥l3,AB=3,BC=2,CD=1,那么下列式子中不成立
的是( ) A.EC∶CG=5∶1 B.EF∶FG=1∶1
C.EF∶FC=3∶2 D.EF∶EG=3∶5
D
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
7.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自
己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知
纸板的两条直角边DE=40 cm,EF=20 cm,测得边DF离地面的高度AC=
1.5 m,CD=8 m,则树高AB是( ) A.4 m B.4.5 m C.5 m D.5.5 m
D
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
8.如图,在平行四边形ABCD中,点E在边CD上,AC与BE相交于点F,若
DE∶CE=1∶2,则△CEF与△ABF的周长比为( ) A.1∶2 B.1∶3 C.2∶3 D.4∶9
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
9.在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规
则,“马”应落在下列哪个位置处,能使“马”“车”“炮”所在位置的格点构成
的三角形与“帅”“相”“兵”所在位置的格点构成的三角形相似( ) A.①处 B.②处 C.③处 D.④处
B
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
10.如图,在△ABC中,AB=AC=18,BC=12,正方形DEFG的顶点E,F在
△ABC内,顶点D,G分别在AB,AC上.若AD=AG,DG=6,则点F到
BC的距离为( ) A.1 B.2 C.12 -6 D.6 -6
D
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
二、填空题(每小题3分,共24分) 11.若 = ,则 = .
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
12.如图,四边形ABCD与四边形EFGH位似,位似中心是点O,若 = ,
则 = .
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
13.如图,在△ABC中,EF∥BC,AD⊥BC交EF于点G,EF=4,BC=5,AD
=3,则AG= .
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
14.如图是用杠杆撬石头的示意图,C是支点,当用力压杠杆的A端时,杠杆
绕点C转动,另一端B向上翘起,石头就被撬动.现有一块石头,要使其
滚动,杠杆的B端必须向上翘起10 cm.已知杠杆的动力臂AC与阻力臂BC之
比为5∶1,要使这块石头滚动,至少要将杠杆的A端向下压 cm.
50
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
15.如图,在 O中,弦AB与弦CD交于点M,且CM∶BM=3∶2,则DM∶AM
= .
2∶3
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
16.如图,在平行四边形ABCD中,E是BC边延长线上一点,AE交CD于点F,
则图中相似三角形有 对.
4
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
17.如图,已知∠ACB=∠ADC=90°,AD=2,CD= ,当AB的长为 .
时,△ACB与△ADC相似.
3或3
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
18.如图,△ABC是面积为27 cm2的等边三角形,被一平行于BC的矩形所截,
AB被截成三等份,则图中阴影部分的面积为 cm2.
9
解析: ∵矩形平行于BC,∴EH∥FG∥BC, ∴△AEH∽△AFG∽△ABC. ∵AB被截成三等份,∴AF=2AE,AB=3AE, ∴S△AEH∶S△AFG∶S△ABC=1∶4∶9, ∴S△AEH∶S四边形EFGH∶S四边形FBCG=1∶3∶5, ∴图中阴影部分的面积S四边形EFGH= ×27=9 (cm2).
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
三、解答题(共66分) 19.(8分)如图,在10×10的网格图中,△ABC三个顶点的坐标分别为A(-4,1),
B(-1,1),C(-2,4). (1)以A为位似中心,将△ABC放大为原来的2倍得到△AB1C1,请在网格图画
出△AB1C1; (2)直接写出(1)中点B1,C1的坐标.
解:(1)如图所示,△AB1C1即为所作.
(2)B1(2,1),C1(0,7).
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
20.(8分)如图,在△ABC中,AB=AC,∠EDF=∠B.求证:△BED∽△CDF.
证明:∵∠EDC=∠EDF+∠FDC=∠B+∠BED,∠EDF=∠B, ∴∠FDC=∠BED. ∵AB=AC, ∴∠B=∠C, ∴△BED∽△CDF.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
21.(8分)如图,EG∥BC,GF∥CD,AE=3,EB=2,AF=6,求AD的长.
解:∵AE=3,EB=2, ∴AB=5. ∵EG∥BC,GF∥CD, ∴ = = , = = . ∵AF=6, ∴AD=10.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
22.(10分)如图,矩形ABCD为台球桌面,AD=280 cm,AB=140 cm,球目前
在点E处,AE=35 cm,如果小丁瞄准BC边上的点F将球打过去,经过反
弹后,球刚好弹到点D处. (1)求证:△BEF∽△CDF;
证明:∵∠EFG=∠DFG, ∴∠EFB=∠DFC. 又∵∠B=∠C=90°, ∴△BEF∽△CDF.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
22.(10分)如图,矩形ABCD为台球桌面,AD=280 cm,AB=140 cm,球目前
在点E处,AE=35 cm,如果小丁瞄准BC边上的点F将球打过去,经过反
弹后,球刚好弹到点D处. (2)求CF的长.
解:∵△BEF∽△CDF, ∴ = . 设FC=x cm,则 = , 解得x=160, ∴CF的长为160 cm.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
23.(10分)如图,在正方形ABCD中,E,F分别是边AD,CD上的点,且E为
AD的中点,FC=3DF,连接EF并延长交BC的延长线于点G. (1)求证:△ABE∽△DEF;
证明:设正方形的边长为4a. ∵E为AD的中点,∴AE=ED=2a. ∵FC=3DF,∴DF=a,FC=3a, ∴ = = . ∵∠A=∠D=90°, ∴△ABE∽△DEF.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)若正方形的边长为4,求△BEG的面积.
解:∵AD=4,∴DE=2. ∵AD∥BC,∴△EDF∽△GCF, ∴ = =3,∴CG=6, ∴BG=BC+CG=10, ∴S△BEG= ×BG×AB=20.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
24.(10分)如图,小明和大伟想利用所学的几何知识测量学校操场上旗杆的高
度,他们的测量方案如下:他们两次利用镜子,第一次他把镜子放在点C
处,人在点F处正好在镜子中看见旗杆顶端A;第二次把镜子放在点D处,
人在点H处正好在镜子中看到旗杆顶端A.已知图中的所有点均在同一平面内,
AB⊥BH,GH⊥BH,EF⊥BH,小明的眼睛距离地面的距离EF=GH=1.68
米,量得CD=10米,CF=2.4米,DH=3.6米,请你利用这些数据求出旗杆
的高度.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
解:根据反射定律可以推出∠ACB=∠ECF,∠ADB=∠GDH. ∵AB⊥BC,EF⊥BC,GH⊥BC, ∴△BAC∽△FEC,△ADB∽△GDH, ∴ = , = . 设AB=x,BC=y,则 = , = ,解得x=14,y=20, 故旗杆的高度为14米.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
25.(12分)在等腰△ABC中,AB=AC=10,BC=12,D为底边BC的中点,以D
为顶点的角∠PDQ=∠B. (1)如图1,若射线DQ经过点A,DP交AC于点E,写出与△CDE相似的三角
形,并说明理由;
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
解:与△CDE相似的三角形为△ABD,△ACD,△ADE.理由如下: ∵AB=AC,D为底边BC的中点, ∴∠B=∠C,AD⊥BC, ∴∠ADB=∠ADC=90°,∴△ABD∽△ACD. ∵∠PDQ=∠B,∴∠PDQ=∠C. 又∵∠DAE=∠CAD,∴△ADE∽△ACD. ∵∠CDE+∠PDQ=90°,∴∠C+∠PDQ=90°,∴∠CED=90°=∠ADC. 又∵∠C=∠C,∴△CDE∽△CAD,∴△ABD∽△ACD∽△ADE∽△CDE.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)如图2,若射线DQ交AB于点F,DP交AC于点E,设AF=x,AE=y,求y与x的
函数关系式;(不要求写出自变量的取值范围)
∴∠EDC=∠BFD,∴△BDF∽△CED,
∴ = . ∵D为BC的中点,∴BD=CD=6,
∴ = ,∴y= .
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(3)在(2)的条件下,连接EF,则△DEF与△CDE相似吗?试说明理由.
△DEF与△CDE相似.理由如下:由(2)可知△BDF∽△CED, ∴ = . ∵BD=CD,∴ = . 又∵∠EDF=∠B=∠C,∴△DEF∽△CDE.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
附加题(20分) 如图,在△ABC中,AB=BC=10,以AB为直径作 O分别交AC,BC于点D,E,连接DE和DB,过点E作EF⊥AB,垂足为F,交BD于点F. (1)求证:AD=DE;
证明:∵AB是 O的直径, ∴∠ADB=90°. 又∵AB=BC, ∴AD=CD= AC,∠ABD=∠CBD, ∴AD=DE.
上一栏目
附加题
(2)若CE=2,求线段CD的长;
解:∵四边形ABED内接于 O, ∴∠CBA=∠CDE. 又∵∠C=∠C, ∴△CDE∽△CBA, ∴ = . ∵AB=BC=10,CE=2,CD= AC, ∴ = . ∴CD= .
上一栏目
附加题
(3)在(2)的条件下,求△DPE的面积.
解:延长EF,交 O于点M.在Rt△ABD中 , ∵AD= ,AB=10,∴BD=3 . ∵AB⊥EM,AB是直径,∴ = , ∴∠BEP=∠EDB,∴△BPE∽△BED,∴ = , 即 = ,∴BP= , ∴DP=BD-BP= , ∴S△DPE∶S△BDE=DP∶BD=13∶45. ∵S△BDC= × ×3 =15,S△BDE∶S△BDC=BE∶BC=4∶5, ∴S△BDE=12,∴S△DPE= .
上一栏目
附加题
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
