人教版九年级 单元卷(三) 旋转 习题课件(共38张PPT)
文档属性
| 名称 | 人教版九年级 单元卷(三) 旋转 习题课件(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 00:00:00 | ||
图片预览






文档简介
单元卷(三) 旋 转
测试范围:第二十三章
选择题
填空题
附加题
解答题
一、选择题(每小题3分,共30分) 1.下列四个交通标志图案中,是中心对称图形的为( ) A.
B.
C.
D.
B
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
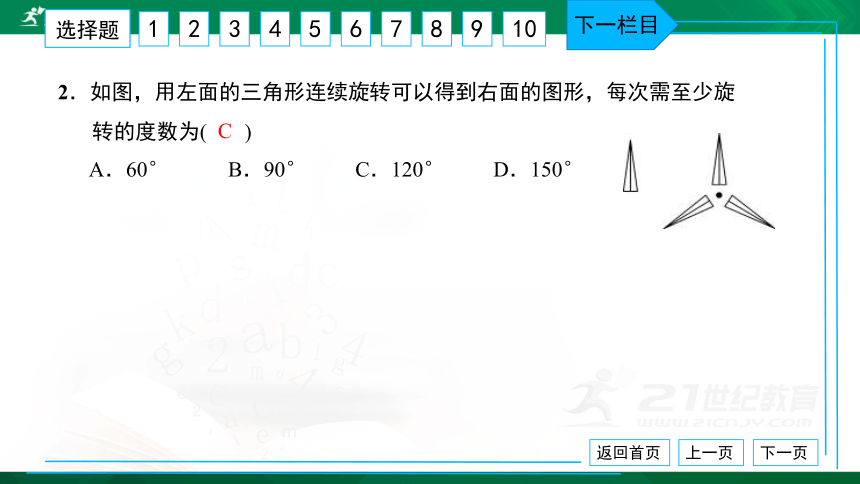
2.如图,用左面的三角形连续旋转可以得到右面的图形,每次需至少旋
转的度数为( ) A.60° B.90° C.120° D.150°
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
3.如图,把△ABC绕点C顺时针旋转某个角度得到△A′B′C,若∠A=30°,
∠1=50°,则∠ACA′等于( ) A.25° B.30° C.19° D.20°
D
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
4.如果点A(3,n)与点B(-m,5)关于原点对称,那么m+n的值为( ) A.8 B.2 C.-2 D.-8
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
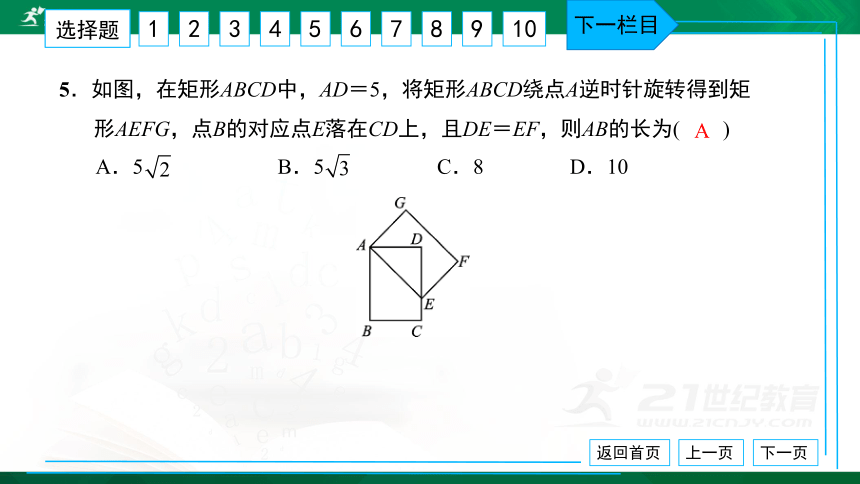
5.如图,在矩形ABCD中,AD=5,将矩形ABCD绕点A逆时针旋转得到矩
形AEFG,点B的对应点E落在CD上,且DE=EF,则AB的长为( ) A.5 B.5 C.8 D.10
A
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
6.如图,在方格纸中选择标有序号①②③④的一个小正方形涂黑,使它与
图中阴影部分组成的新图案为中心对称图形,该小正方形的序号是( ) A.① B.② C.③ D.④
B
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
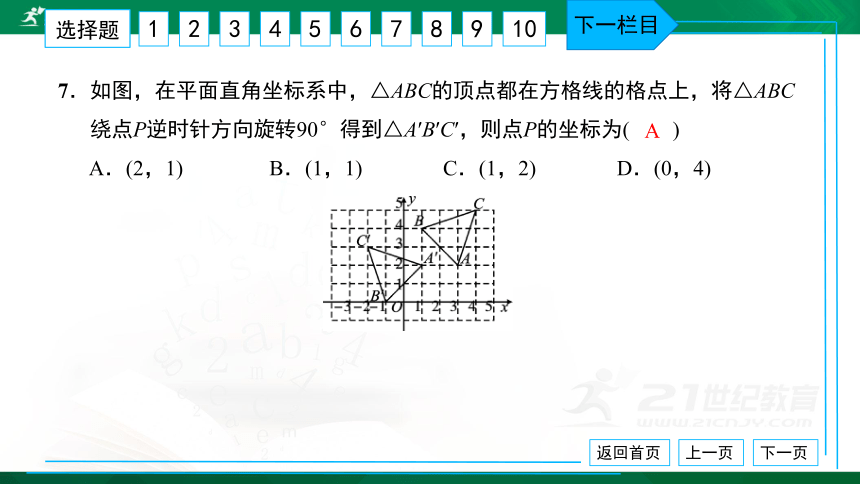
7.如图,在平面直角坐标系中,△ABC的顶点都在方格线的格点上,将△ABC
绕点P逆时针方向旋转90°得到△A′B′C′,则点P的坐标为( ) A.(2,1) B.(1,1) C.(1,2) D.(0,4)
A
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
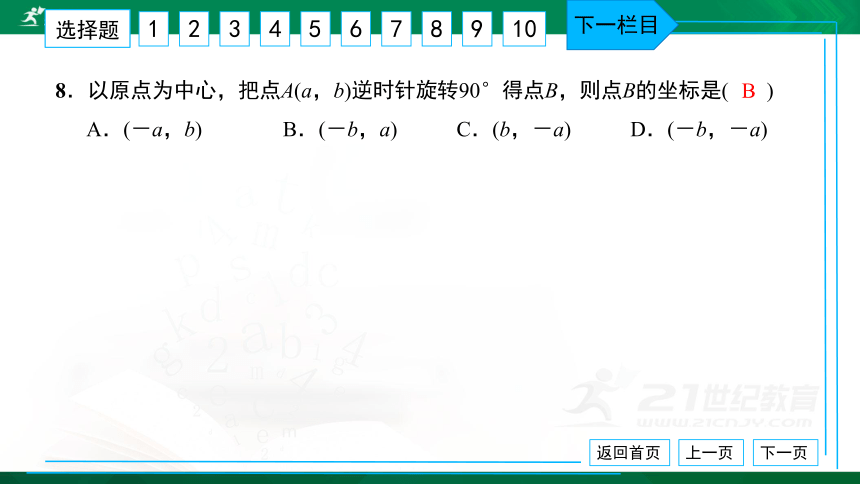
8.以原点为中心,把点A(a,b)逆时针旋转90°得点B,则点B的坐标是( ) A.(-a,b) B.(-b,a) C.(b,-a) D.(-b,-a)
B
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
9.如图,在等边△ABC中,AC=10,点O在AC上,且AO=3,P是AB上一动
点,连接OP,将线段OP绕点O逆时针旋转60°得到线段OD.要使点D恰好
落在BC上,则AP的长是( ) A.5 B.6 C.7 D.9
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
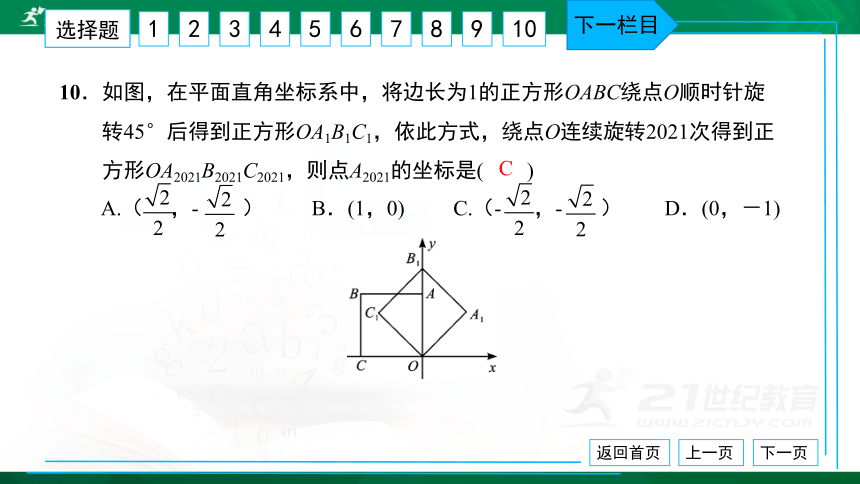
10.如图,在平面直角坐标系中,将边长为1的正方形OABC绕点O顺时针旋
转45°后得到正方形OA1B1C1,依此方式,绕点O连续旋转2021次得到正
方形OA2021B2021C2021,则点A2021的坐标是( ) A.( ,- ) B.(1,0) C.(- ,- ) D.(0,-1)
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
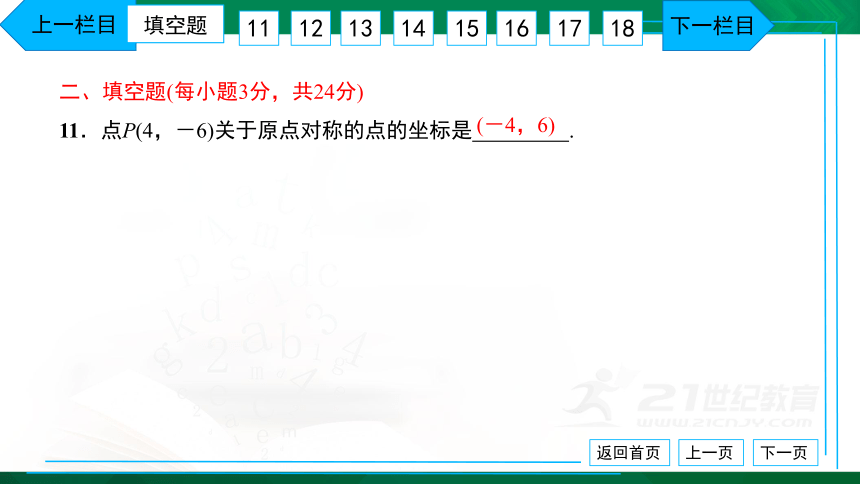
二、填空题(每小题3分,共24分) 11.点P(4,-6)关于原点对称的点的坐标是 .
(-4,6)
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
12.在等边三角形、正方形、直角三角形、等腰梯形中,既是轴对称图形又是
中心对称图形的是 .
正方形
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
13.如图,△ABC为等边三角形,D为BC边上一点,△ABD经过逆时针旋转后
得到△ACP,则旋转中心是点 ,旋转角的大小是 .
A
60°
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
14.若点P(1-2a,a-2)关于原点的对称点在第一象限内,a为整数,则a的
值为 .
1
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
15.如图,将Rt△ABC绕直角顶点C顺时针旋转90°得到△A′B′C,连接BB′,
若∠A′B′B=20°,则∠A的度数是 .
65°
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
16.如图,点O,A,B都在正方形网格的格点上,将△OAB绕点O顺时针旋
转后得到△OA′B′,点A,B的对应点A′,B′也在格点上,则旋转角α(0°
<α<180°)的度数为 °.
90
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
17.如图,在△ABC中,∠ACB=90°,∠B=60°,BC=2.将△ABC绕点C
顺时针旋转得到△A′B′C,连接AB′,且A,B′,A′在同一条直线上,则AA′
= .
6
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
18.如图,在矩形ABCD中,O是对角线AC的中点.将矩形ABCD绕点B顺时
针旋转90°,旋转后的四边形为A′BC′D′,点O的对应点为点O′.若AB=8,
BC=10,则线段CO′的长为 .
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
三、解答题(共66分) 19.(9分)如图,△ABC与△ADE关于点A成中心对称. (1)写出点A,B,C的对应点; (2)判断C,A,E的位置关系; (3)写出图中相等的线段和相等的角.
解: (1)点A,B,C的对应点分别是点A,D,E.
(2)点C,A,E在同一条直线上.
(3)AB=AD,AC=AE,BC=DE,∠B=∠D,∠C=∠E,∠BAC=∠DAE, ∠CAD=∠BAE.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
20.(8分)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,-4),
B(3,-3),C(1,-1).(每个小方格都是边长为一个单位长度的正方形) (1)画出△ABC关于原点对称的图形△A1B1C1,并写出A1,B1,C1的坐标; (2)画出△ABC绕点B逆时针旋转90°后得到的图形△A2B2C2.
解:(1)△A1B1C1如图所示,点A1,B1,C1的坐标分别为(-1,4),(-3,3),(-1,1). (2)△A2B2C2如图所示.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
21.(8分)如图,E是正方形ABCD的边DC上一点,把△ADE顺时针旋转到△ABF
的位置. (1)旋转中心是点 ,旋转角度是 度; (2)连接EF,则△AEF是 三角形,并给予证明.
证明如下: 由旋转的性质,得AF=AE,∠FAB=∠EAD, ∴∠FAB+∠BAE=∠EAD+∠BAE,即∠FAE=∠BAD. ∵四边形ABCD是正方形,∴∠FAE=∠BAD=90°, ∴△AEF是等腰直角三角形.
A
90
等腰直角
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
22.(9分)如图,直线y= x+3交x轴于点B,交y轴于点A,点C与点A,点D与点B
分别关于原点对称. (1)求点C,D的坐标;
解:(1)在y= x+3中, 令x=0,则y=3,令y=0,则x=-2, ∴点A的坐标为(0,3),点B的坐标为(-2,0). ∵点C与点A,点D与点B分别关于原点对称, ∴点C的坐标为(0,-3),点D的坐标为(2,0).
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)线段CD可看作是线段AB绕着点 旋转 得到的; (3)求四边形ABCD的面积.
O
180°
解:S四边形ABCD=S△ABO+S△ADO+S△CDO+S△COB=4S△ABO=4× ×2×3=12.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
23.(10分)如图,在△ABC中,AB=BC,将△ABC绕顶点B逆时针旋转α到△A′BC′
的位置,AB与A′C′相交于点D,AC与A′C′,BC′分别相交于点E,F. (1)求证:△BCF △BA′D;
证明:∵AB=BC,∴∠A=∠C. 由旋转的性质,得 A′B=AB=BC,∠A′=∠A=∠C,∠A′BD=∠CBC′. 在△BCF与△BA′D中,
∴△BCF △BA′D.
∠C=∠A′,
BC=A′B,
∠CBF=∠A′BD,
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)当∠C=α时,判断四边形A′BCE的形状,并说明理由.
解:四边形A′BCE是菱形.理由如下: 由题意,得∠A′=∠A=∠C=α,∠A′BD=α. ∵∠ADE=∠A′DB, ∴∠AED=∠A′BD=α, ∴∠DEC=180°-α. ∴∠A′BC=360°-∠A′-∠C-∠A′EC=180°-α, ∴∠A′BC=∠A′EC. 又∵∠A′=∠C, ∴四边形A′BCE是平行四边形. ∵A′B=BC, ∴四边形A′BCE是菱形.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
24.(10分)如图,在△ABC中,AB=AC,把△ABC绕点A顺时针旋转得到△ADE
(点B,C分别对应点D,E),BD和CE交于点F. (1)求证:CE=BD;
证明:由旋转的性质,得 AD=AB,AE=AC,∠DAE=∠BAC, ∴∠DAE+∠BAE=∠BAC+∠BAE, 即∠DAB=∠EAC. ∵AB=AC,∴AD=AB=AC=AE, ∴△AEC △ADB(SAS),∴CE=BD.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)若AB=2,∠BAC=45°,当四边形ADFC是平行四边形时,求BF的长.
解:∵四边形ADFC是平行四边形, ∴AC=DF,AC∥BD,∴∠ABD=∠BAC=45°. ∵AB=AD,∴∠ADB=∠ABD=45°, ∴∠BAD=90°,∴BD= AB=2 . ∵DF=AC=AB=2,∴BF=BD-DF=2 -2.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
25.(12分)已知O是△ABC内一点,连接OA,OB,OC. (1)如图1,若△ABC是等边三角形,且OA=3,OB=4,OC=5,将△BAO
绕点B顺时针旋转后,得到△BCD,连接OD. ①旋转角的度数为 ; ②线段OD的长为 ;
60°
4
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
③求∠BDC的度数.
解:③由旋转的性质,得∠ABO=∠CBO, ∴∠ABO+∠OBC=∠OBC+∠CBD.即∠ABC=∠OBD=60°. 又∵OB=BD,∴△BOD为等边三角形,∴∠BDO=60°. 由旋转的性质,得CD=OA=3. 在△OCD中,CD=3,OD=4,OC=5, ∴CD2+OD2=OC2,∴△OCD为直角三角形,且∠ODC=90°, ∴∠BDC=∠BDO+∠ODC=60°+90°=150°.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)如图2,若△ABC是等腰直角三角形,且∠ABC=90°,将△BAO绕点B顺时
针旋转后,得到△BCD,连接OD.当OA,OB,OC满足什么条件时,∠ODC
=90°?请给出证明.
当OA2+2OB2=OC2时,∠ODC=90°.证明如下: 由旋转的性质,得∠ABO=∠CBD, ∴∠OBD=∠ABC=90°,OB=BD,CD=AO, ∴△OBD为等腰直角三角形,∴OD= =OB. ∵当CD2+OD2=OC2时,△OCD为直角三角形,∠ODC=90°, ∴OA2+2OB2=OC2, ∴当OA,OB,OC满足OA2+2OB2=OC2时,∠ODC=90°.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
附加题(20分) 将两块斜边长相等的等腰直角三角板ACB和CDE按如图1摆放,斜边AB分别交CD,CE于点M,N.
上一栏目
附加题
(1)如图2,把图1中的△BCN绕点C逆时针旋转90°得到△ACF,连接FM,求
证:△CMF △CMN;
(1)证明:由旋转性质,得 ∴CF=CN,∠ACF=∠BCN. ∵△ACB和△DCE是等腰直角三角形, ∴∠ACB=90°,∠DCE=45°, ∴∠ACM+∠BCN=∠ACB-∠DCE=90°-45°=45°, ∴∠ACM+∠ACF=45°,即∠MCF=45°,∴∠MCF=∠MCN. 在△CMF和△CMN中,
∴△CMF △CMN.
CF=CN,
∠MCF=∠MCN,
CM=CM,
上一栏目
附加题
(2)将△CED绕点C旋转. ①当点M,N在AB上(不与点A,B重合)时,线段AM,MN与BN之间有一个不变
的关系式,请你写出这个关系式,并说明理由;
①AM2+BN2=MN2.理由如下: 由(1)知△CMF △CMN,∴MF=MN. ∵△ACB是等腰直角三角形, ∴∠B=∠BAC=45°. 由旋转的性质,得AF=BN,∠CAF=∠B=45°, ∴∠FAM=∠CAF+∠BAC=45°+45°=90°, ∴AM2+AF2=MF2,∴AM2+BN2=MN2.
上一栏目
附加题
②如图3,当点M在AB上,点N在AB的延长线上时,①中的关系式是否仍然成
立?请说明理由.
②仍然成立.理由如下: 如图,把△BCN绕点C逆时针旋转90°,得到△ACF, 则AF=BN,CF=CN,∠BCN=∠ACF. ∵∠MCF=∠ACB-∠MCB-∠ACF =90°-(45°-∠BCN)-∠ACF =45°+∠BCN-∠ACF=45°, ∴∠MCF=∠MCN.
上一栏目
附加题
②如图3,当点M在AB上,点N在AB的延长线上时,①中的关系式是否仍然成
立?请说明理由.
在△CMF和△CMN中, ∴△CMF △CMN,∴MF=MN. ∵∠ABC=45°,∴∠CAF=∠CBN=180°-∠ABC=135°. 又∵∠BAC=45°,∴∠FAM=∠CAF-∠BAC=90°, ∴AM2+AF2=MF2,∴AM2+BN2=MN2.
CF=CN,
∠MCF=∠MCN,
CM=CM,
上一栏目
附加题
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
测试范围:第二十三章
选择题
填空题
附加题
解答题
一、选择题(每小题3分,共30分) 1.下列四个交通标志图案中,是中心对称图形的为( ) A.
B.
C.
D.
B
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
2.如图,用左面的三角形连续旋转可以得到右面的图形,每次需至少旋
转的度数为( ) A.60° B.90° C.120° D.150°
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
3.如图,把△ABC绕点C顺时针旋转某个角度得到△A′B′C,若∠A=30°,
∠1=50°,则∠ACA′等于( ) A.25° B.30° C.19° D.20°
D
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
4.如果点A(3,n)与点B(-m,5)关于原点对称,那么m+n的值为( ) A.8 B.2 C.-2 D.-8
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
5.如图,在矩形ABCD中,AD=5,将矩形ABCD绕点A逆时针旋转得到矩
形AEFG,点B的对应点E落在CD上,且DE=EF,则AB的长为( ) A.5 B.5 C.8 D.10
A
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
6.如图,在方格纸中选择标有序号①②③④的一个小正方形涂黑,使它与
图中阴影部分组成的新图案为中心对称图形,该小正方形的序号是( ) A.① B.② C.③ D.④
B
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
7.如图,在平面直角坐标系中,△ABC的顶点都在方格线的格点上,将△ABC
绕点P逆时针方向旋转90°得到△A′B′C′,则点P的坐标为( ) A.(2,1) B.(1,1) C.(1,2) D.(0,4)
A
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
8.以原点为中心,把点A(a,b)逆时针旋转90°得点B,则点B的坐标是( ) A.(-a,b) B.(-b,a) C.(b,-a) D.(-b,-a)
B
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
9.如图,在等边△ABC中,AC=10,点O在AC上,且AO=3,P是AB上一动
点,连接OP,将线段OP绕点O逆时针旋转60°得到线段OD.要使点D恰好
落在BC上,则AP的长是( ) A.5 B.6 C.7 D.9
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
10.如图,在平面直角坐标系中,将边长为1的正方形OABC绕点O顺时针旋
转45°后得到正方形OA1B1C1,依此方式,绕点O连续旋转2021次得到正
方形OA2021B2021C2021,则点A2021的坐标是( ) A.( ,- ) B.(1,0) C.(- ,- ) D.(0,-1)
C
选择题
1
2
3
4
5
6
7
8
9
10
下一栏目
二、填空题(每小题3分,共24分) 11.点P(4,-6)关于原点对称的点的坐标是 .
(-4,6)
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
12.在等边三角形、正方形、直角三角形、等腰梯形中,既是轴对称图形又是
中心对称图形的是 .
正方形
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
13.如图,△ABC为等边三角形,D为BC边上一点,△ABD经过逆时针旋转后
得到△ACP,则旋转中心是点 ,旋转角的大小是 .
A
60°
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
14.若点P(1-2a,a-2)关于原点的对称点在第一象限内,a为整数,则a的
值为 .
1
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
15.如图,将Rt△ABC绕直角顶点C顺时针旋转90°得到△A′B′C,连接BB′,
若∠A′B′B=20°,则∠A的度数是 .
65°
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
16.如图,点O,A,B都在正方形网格的格点上,将△OAB绕点O顺时针旋
转后得到△OA′B′,点A,B的对应点A′,B′也在格点上,则旋转角α(0°
<α<180°)的度数为 °.
90
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
17.如图,在△ABC中,∠ACB=90°,∠B=60°,BC=2.将△ABC绕点C
顺时针旋转得到△A′B′C,连接AB′,且A,B′,A′在同一条直线上,则AA′
= .
6
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
18.如图,在矩形ABCD中,O是对角线AC的中点.将矩形ABCD绕点B顺时
针旋转90°,旋转后的四边形为A′BC′D′,点O的对应点为点O′.若AB=8,
BC=10,则线段CO′的长为 .
上一栏目
填空题
11
12
13
14
15
16
17
18
下一栏目
三、解答题(共66分) 19.(9分)如图,△ABC与△ADE关于点A成中心对称. (1)写出点A,B,C的对应点; (2)判断C,A,E的位置关系; (3)写出图中相等的线段和相等的角.
解: (1)点A,B,C的对应点分别是点A,D,E.
(2)点C,A,E在同一条直线上.
(3)AB=AD,AC=AE,BC=DE,∠B=∠D,∠C=∠E,∠BAC=∠DAE, ∠CAD=∠BAE.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
20.(8分)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,-4),
B(3,-3),C(1,-1).(每个小方格都是边长为一个单位长度的正方形) (1)画出△ABC关于原点对称的图形△A1B1C1,并写出A1,B1,C1的坐标; (2)画出△ABC绕点B逆时针旋转90°后得到的图形△A2B2C2.
解:(1)△A1B1C1如图所示,点A1,B1,C1的坐标分别为(-1,4),(-3,3),(-1,1). (2)△A2B2C2如图所示.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
21.(8分)如图,E是正方形ABCD的边DC上一点,把△ADE顺时针旋转到△ABF
的位置. (1)旋转中心是点 ,旋转角度是 度; (2)连接EF,则△AEF是 三角形,并给予证明.
证明如下: 由旋转的性质,得AF=AE,∠FAB=∠EAD, ∴∠FAB+∠BAE=∠EAD+∠BAE,即∠FAE=∠BAD. ∵四边形ABCD是正方形,∴∠FAE=∠BAD=90°, ∴△AEF是等腰直角三角形.
A
90
等腰直角
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
22.(9分)如图,直线y= x+3交x轴于点B,交y轴于点A,点C与点A,点D与点B
分别关于原点对称. (1)求点C,D的坐标;
解:(1)在y= x+3中, 令x=0,则y=3,令y=0,则x=-2, ∴点A的坐标为(0,3),点B的坐标为(-2,0). ∵点C与点A,点D与点B分别关于原点对称, ∴点C的坐标为(0,-3),点D的坐标为(2,0).
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)线段CD可看作是线段AB绕着点 旋转 得到的; (3)求四边形ABCD的面积.
O
180°
解:S四边形ABCD=S△ABO+S△ADO+S△CDO+S△COB=4S△ABO=4× ×2×3=12.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
23.(10分)如图,在△ABC中,AB=BC,将△ABC绕顶点B逆时针旋转α到△A′BC′
的位置,AB与A′C′相交于点D,AC与A′C′,BC′分别相交于点E,F. (1)求证:△BCF △BA′D;
证明:∵AB=BC,∴∠A=∠C. 由旋转的性质,得 A′B=AB=BC,∠A′=∠A=∠C,∠A′BD=∠CBC′. 在△BCF与△BA′D中,
∴△BCF △BA′D.
∠C=∠A′,
BC=A′B,
∠CBF=∠A′BD,
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)当∠C=α时,判断四边形A′BCE的形状,并说明理由.
解:四边形A′BCE是菱形.理由如下: 由题意,得∠A′=∠A=∠C=α,∠A′BD=α. ∵∠ADE=∠A′DB, ∴∠AED=∠A′BD=α, ∴∠DEC=180°-α. ∴∠A′BC=360°-∠A′-∠C-∠A′EC=180°-α, ∴∠A′BC=∠A′EC. 又∵∠A′=∠C, ∴四边形A′BCE是平行四边形. ∵A′B=BC, ∴四边形A′BCE是菱形.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
24.(10分)如图,在△ABC中,AB=AC,把△ABC绕点A顺时针旋转得到△ADE
(点B,C分别对应点D,E),BD和CE交于点F. (1)求证:CE=BD;
证明:由旋转的性质,得 AD=AB,AE=AC,∠DAE=∠BAC, ∴∠DAE+∠BAE=∠BAC+∠BAE, 即∠DAB=∠EAC. ∵AB=AC,∴AD=AB=AC=AE, ∴△AEC △ADB(SAS),∴CE=BD.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)若AB=2,∠BAC=45°,当四边形ADFC是平行四边形时,求BF的长.
解:∵四边形ADFC是平行四边形, ∴AC=DF,AC∥BD,∴∠ABD=∠BAC=45°. ∵AB=AD,∴∠ADB=∠ABD=45°, ∴∠BAD=90°,∴BD= AB=2 . ∵DF=AC=AB=2,∴BF=BD-DF=2 -2.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
25.(12分)已知O是△ABC内一点,连接OA,OB,OC. (1)如图1,若△ABC是等边三角形,且OA=3,OB=4,OC=5,将△BAO
绕点B顺时针旋转后,得到△BCD,连接OD. ①旋转角的度数为 ; ②线段OD的长为 ;
60°
4
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
③求∠BDC的度数.
解:③由旋转的性质,得∠ABO=∠CBO, ∴∠ABO+∠OBC=∠OBC+∠CBD.即∠ABC=∠OBD=60°. 又∵OB=BD,∴△BOD为等边三角形,∴∠BDO=60°. 由旋转的性质,得CD=OA=3. 在△OCD中,CD=3,OD=4,OC=5, ∴CD2+OD2=OC2,∴△OCD为直角三角形,且∠ODC=90°, ∴∠BDC=∠BDO+∠ODC=60°+90°=150°.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
(2)如图2,若△ABC是等腰直角三角形,且∠ABC=90°,将△BAO绕点B顺时
针旋转后,得到△BCD,连接OD.当OA,OB,OC满足什么条件时,∠ODC
=90°?请给出证明.
当OA2+2OB2=OC2时,∠ODC=90°.证明如下: 由旋转的性质,得∠ABO=∠CBD, ∴∠OBD=∠ABC=90°,OB=BD,CD=AO, ∴△OBD为等腰直角三角形,∴OD= =OB. ∵当CD2+OD2=OC2时,△OCD为直角三角形,∠ODC=90°, ∴OA2+2OB2=OC2, ∴当OA,OB,OC满足OA2+2OB2=OC2时,∠ODC=90°.
上一栏目
解答题
19
20
21
22
23
24
25
下一栏目
附加题(20分) 将两块斜边长相等的等腰直角三角板ACB和CDE按如图1摆放,斜边AB分别交CD,CE于点M,N.
上一栏目
附加题
(1)如图2,把图1中的△BCN绕点C逆时针旋转90°得到△ACF,连接FM,求
证:△CMF △CMN;
(1)证明:由旋转性质,得 ∴CF=CN,∠ACF=∠BCN. ∵△ACB和△DCE是等腰直角三角形, ∴∠ACB=90°,∠DCE=45°, ∴∠ACM+∠BCN=∠ACB-∠DCE=90°-45°=45°, ∴∠ACM+∠ACF=45°,即∠MCF=45°,∴∠MCF=∠MCN. 在△CMF和△CMN中,
∴△CMF △CMN.
CF=CN,
∠MCF=∠MCN,
CM=CM,
上一栏目
附加题
(2)将△CED绕点C旋转. ①当点M,N在AB上(不与点A,B重合)时,线段AM,MN与BN之间有一个不变
的关系式,请你写出这个关系式,并说明理由;
①AM2+BN2=MN2.理由如下: 由(1)知△CMF △CMN,∴MF=MN. ∵△ACB是等腰直角三角形, ∴∠B=∠BAC=45°. 由旋转的性质,得AF=BN,∠CAF=∠B=45°, ∴∠FAM=∠CAF+∠BAC=45°+45°=90°, ∴AM2+AF2=MF2,∴AM2+BN2=MN2.
上一栏目
附加题
②如图3,当点M在AB上,点N在AB的延长线上时,①中的关系式是否仍然成
立?请说明理由.
②仍然成立.理由如下: 如图,把△BCN绕点C逆时针旋转90°,得到△ACF, 则AF=BN,CF=CN,∠BCN=∠ACF. ∵∠MCF=∠ACB-∠MCB-∠ACF =90°-(45°-∠BCN)-∠ACF =45°+∠BCN-∠ACF=45°, ∴∠MCF=∠MCN.
上一栏目
附加题
②如图3,当点M在AB上,点N在AB的延长线上时,①中的关系式是否仍然成
立?请说明理由.
在△CMF和△CMN中, ∴△CMF △CMN,∴MF=MN. ∵∠ABC=45°,∴∠CAF=∠CBN=180°-∠ABC=135°. 又∵∠BAC=45°,∴∠FAM=∠CAF-∠BAC=90°, ∴AM2+AF2=MF2,∴AM2+BN2=MN2.
CF=CN,
∠MCF=∠MCN,
CM=CM,
上一栏目
附加题
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
