直线和圆的位置关系

(共16张PPT)
复习提问：
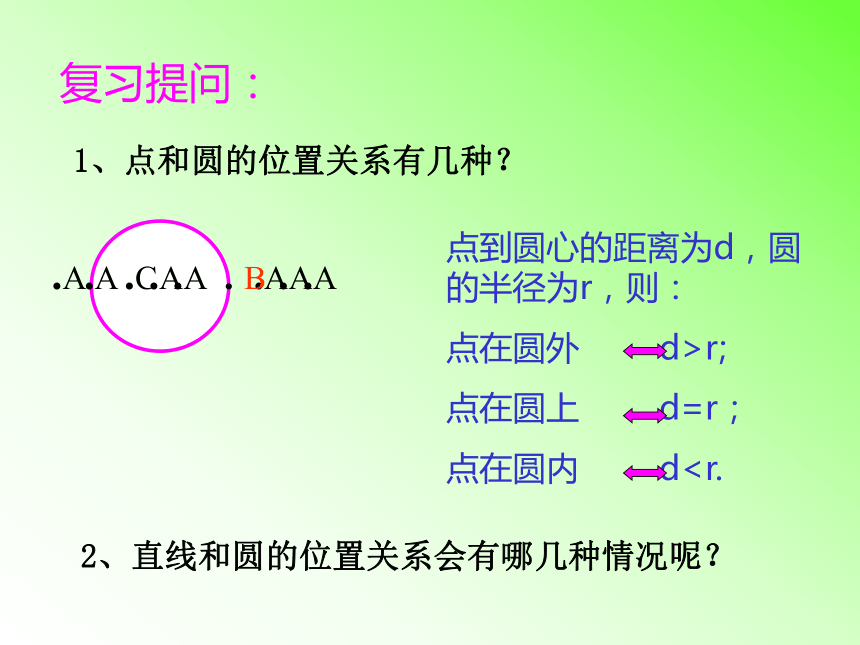
1、点和圆的位置关系有几种？
.A
.A
.A
. B
.A
.A
.C
.A
.A
点到圆心的距离为d，圆的半径为r，则：
点在圆外 d>r;
点在圆上 d=r；
点在圆内 d2、直线和圆的位置关系会有哪几种情况呢？
太阳与地平线的位置关系,列车的轮子与铁轨之间的关系,都给我们直线与圆的位置关系的印象.
试一试
. 在纸上画一个圆，把直尺看作直线，
移动直尺。
你能发现直线与圆的公共点个数的变化情况吗？公共点最少时有几个？最多时有几个？
l5
l4
l3
l2
l1
l8
l9
l7
l6
通过实验，你认为直线和圆的位置关系会有哪几种情况？
.O
l
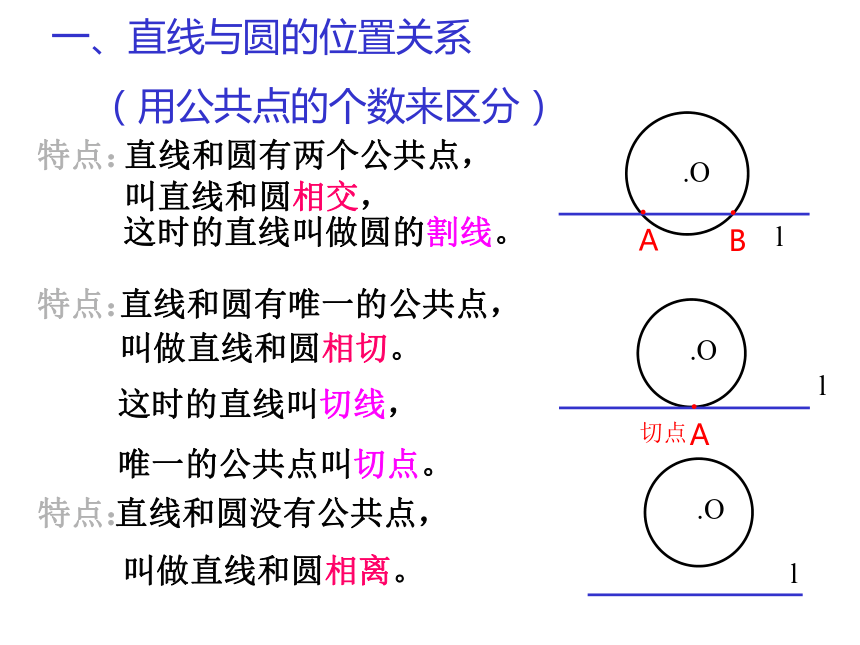
特点：
.O
叫做直线和圆相离。
直线和圆没有公共点，
l
特点：
直线和圆有唯一的公共点，
叫做直线和圆相切。
这时的直线叫切线，
唯一的公共点叫切点。
.O
l
特点：
直线和圆有两个公共点，
叫直线和圆相交，
这时的直线叫做圆的割线。
一、直线与圆的位置关系
（用公共点的个数来区分）
.A
.A
.B
切点
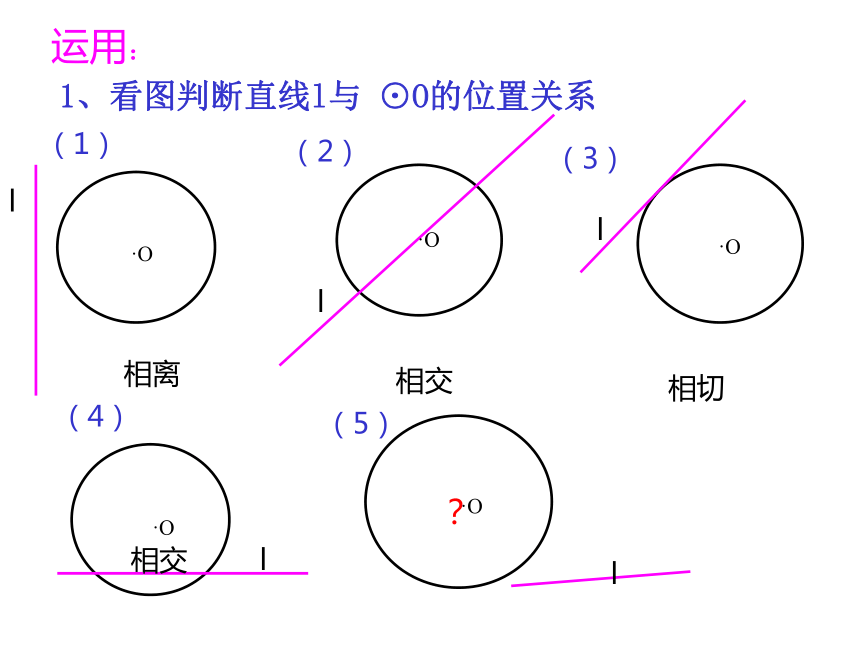
运用：
1、看图判断直线l与 ⊙O的位置关系
（1）
（2）
（3）
（4）
（5）
相离
相切
相交
相交
？
l
l
l
l
l
·O
·O
·O
·O
·O
（5）
如果，公共点的个数不好判断，该怎么办？
“直线和圆的位置关系”能否像“点和圆的位置关系”一样进行数量分析？
？
l
·O
·
A
·
B
．Ｏ
l
┐
d
r
．ｏ
l
2、直线和圆相切
┐
d
r
d = r
．O
l
3、直线和圆相交
d < r
d
┐
r
二、直线和圆的位置关系（用圆心o到直线l的距离d与圆的半径r的关系来区分）
1、直线和圆相离
d > r
二、直线与圆的位置关系的性质和判定
解决问题1: 设⊙O的半径为r，直线a上一点到圆心的距离为d，若d=r，则直线a与⊙O的位置关系是（ ）
（A）相交 （B）相切 （C）相离 （D）相切或相交
D

解决问题2:已知圆的半径等于5,直线l与圆没有交点,则圆心到直线的距离d的取值范围是 .
解决问题3:直线l与半径为r的⊙O相交,且点O到直线l的距离为8,则r的取值范围是 .
d>5
r>8
思考：求圆心A到X轴、
Y轴的距离各是多少
A.(-3,-4)
O
X
Y
解决问题4: 已知⊙A的直径为6，点A的坐标为
（-3，-4），则X轴与⊙A的位置关系是_____, Y轴与⊙A的位置关系是______。
B
C
4
3
相离
相切
解决问题5: 在Rt△ABC中，∠C=90°，AC=3cm，BC=4cm。以C为圆心，r为半径的圆与AB有怎样的位置关系？为什么？
(1)r=2cm (2)r=2.4cm (3)r=3cm
B
4
C 3 A
D
解：圆心C到AB的距离d=2.4cm
(1)当r=2cm时,
有d>r,
因此⊙C和AB相离。
5
2.4
思考：图中线段AB的长度为多少？
.
(2)当r=2.4cm 时,
有d=r,
因此⊙C和AB相切。
D
B
C A
2.4
(3)当r=3cm 时，
有d因此⊙C和AB相交。
D
B
C A
2.4
怎样求圆心C到直线AB的距离？
说说收获
直线与圆的位置关系
直线与圆的
位置关系 相交 相切 相离
图 形
公共点个数
公共点名称
直线名称
圆心到直线距离d与半径r的关系
2 个
交点
割线
1 个
切点
切线
d < r
d = r
d > r
没有
判定直线 与圆的位置关系的方法有____种：
（1）根据定义，由__________________的个数来判断；
（2）根据性质，_____________________ ______________的关系来判断。
在实际应用中，常采用第二种方法判定。
两
直线 与圆的公共点
圆心到直线的距离d
与半径r
小结：
随堂检测
1．⊙O的半径为3 ,圆心O到直线l的距离为d,若直线l　
　与⊙O没有公共点，则d为（　）：
　A．d ＞3 B．d<3 C．d ≤3 D．d =3
2．圆心O到直线的距离等于⊙O的半径，则直线
和⊙O的位置 关系是（　　）：
A．相离 B.相交 C.相切 D.相切或相交
3.判断:若直线和圆相切,则该直线和圆一定有一个公共点.( )
4.等边三角形ABC的边长为2,则以A为圆心,半径为1.73的圆
与直线BC的位置关系是 ,以A为圆心,
为半径的圆与直线BC相切.
A
C
√
相离
思考题:已知点A的坐标为(1,2),⊙A的半径为3.
(1)若要使⊙A与y轴相切,则要把⊙A向右平移几个单 位 此时,⊙A与x轴、⊙A与点O分别有怎样的位置关系 若把⊙A向左平移呢
(2)若要使⊙A与x轴、y轴都相切,则圆心A应当移到 什么位置 请写出点A所有可能位置的坐标.