人教版数学八年级上册 第12章 12.1全等三角形同步测试题(一)(Word版 含解析)
文档属性
| 名称 | 人教版数学八年级上册 第12章 12.1全等三角形同步测试题(一)(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 146.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-26 17:04:31 | ||
图片预览


文档简介
全等三角形同步测试题(一)
一.选择题
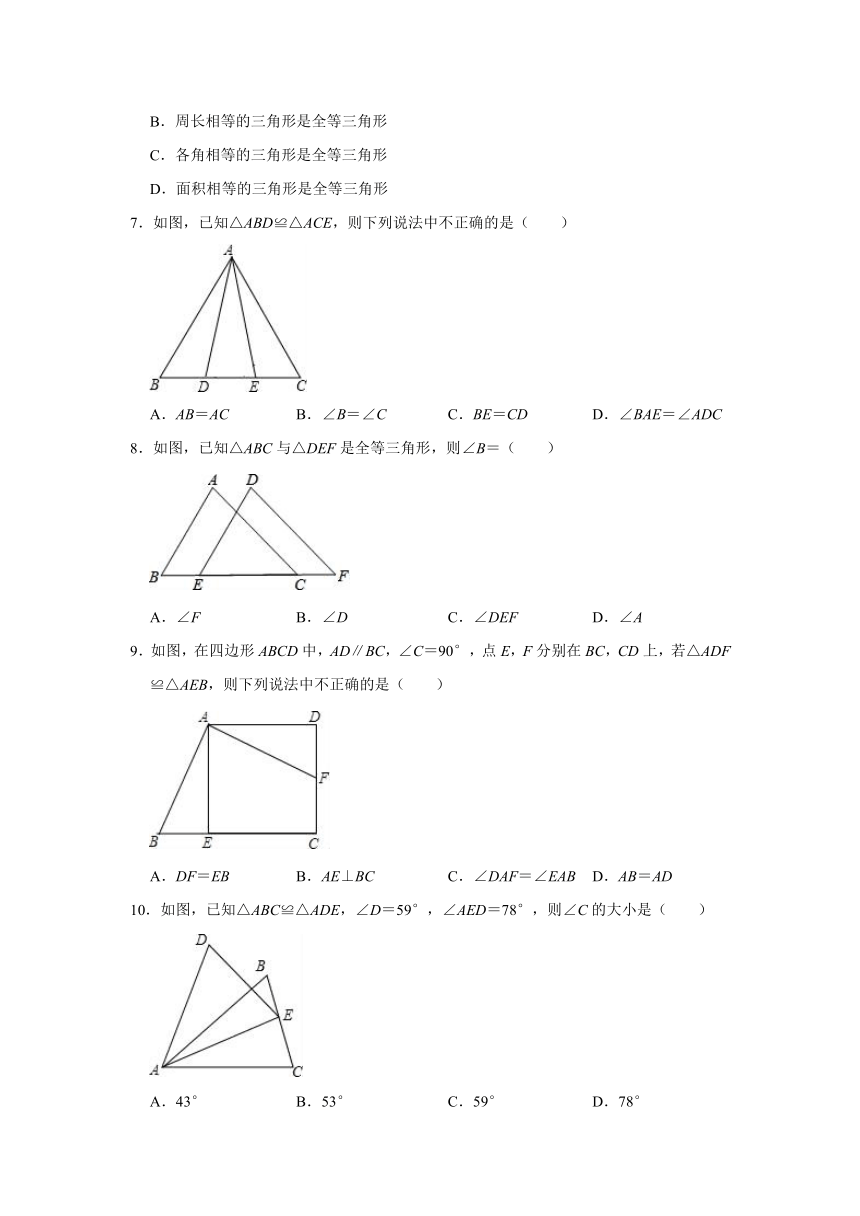
1.如图,△ABC≌△BAD,若AB=6,AC=4,BC=5,则AD的长为( )
A.4 B.5 C.6 D.以上都不对
2.下列说法错误的是( )
A.两个面积相等的圆一定全等
B.全等三角形是指形状、大小都相同的三角形
C.底边相等的两个等腰三角形全等
D.斜边上中线和一条直角边对应相等的两直角三角形全等
3.全等图形是指两个图形( )
A.能够重合 B.形状相同 C.大小相同 D.相等
4.如图,△ABC≌△EFD,AB=EF,AE=15,CD=3,则AC=( )
A.5 B.6 C.9 D.12
5.如图,△ABC≌△AED,点D落在BC上,且∠B=60°,则∠EDC的度数等于( )
A.45° B.30° C.60° D.75°
6.下列说法正确的是( )
A.能够完全重合的两个图形叫做全等图形
B.周长相等的三角形是全等三角形
C.各角相等的三角形是全等三角形
D.面积相等的三角形是全等三角形
7.如图,已知△ABD≌△ACE,则下列说法中不正确的是( )
A.AB=AC B.∠B=∠C C.BE=CD D.∠BAE=∠ADC
8.如图,已知△ABC与△DEF是全等三角形,则∠B=( )
A.∠F B.∠D C.∠DEF D.∠A
9.如图,在四边形ABCD中,AD∥BC,∠C=90°,点E,F分别在BC,CD上,若△ADF≌△AEB,则下列说法中不正确的是( )
A.DF=EB B.AE⊥BC C.∠DAF=∠EAB D.AB=AD
10.如图,已知△ABC≌△ADE,∠D=59°,∠AED=78°,则∠C的大小是( )
A.43° B.53° C.59° D.78°
二.填空题
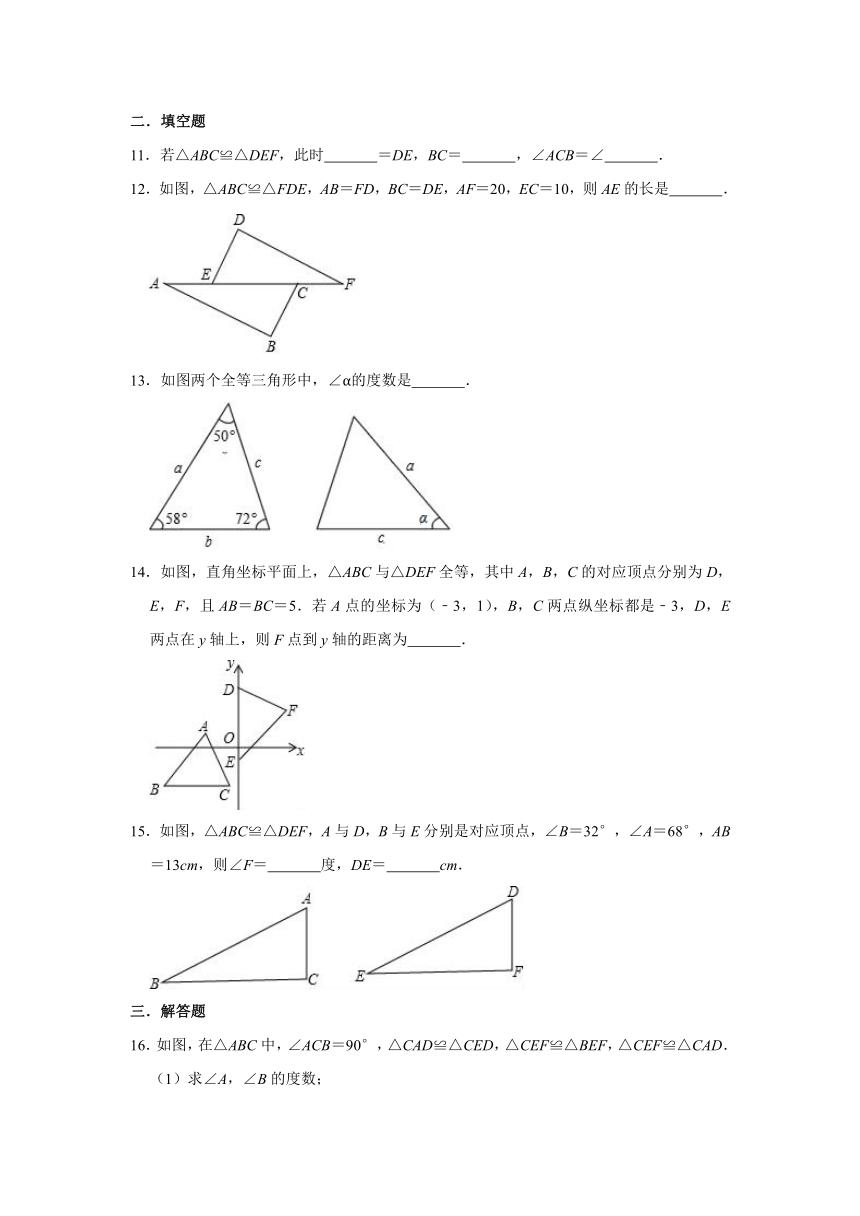
11.若△ABC≌△DEF,此时 =DE,BC= ,∠ACB=∠ .
12.如图,△ABC≌△FDE,AB=FD,BC=DE,AF=20,EC=10,则AE的长是 .
13.如图两个全等三角形中,∠α的度数是 .
14.如图,直角坐标平面上,△ABC与△DEF全等,其中A,B,C的对应顶点分别为D,E,F,且AB=BC=5.若A点的坐标为(﹣3,1),B,C两点纵坐标都是﹣3,D,E两点在y轴上,则F点到y轴的距离为 .
15.如图,△ABC≌△DEF,A与D,B与E分别是对应顶点,∠B=32°,∠A=68°,AB=13cm,则∠F= 度,DE= cm.
三.解答题
16.如图,在△ABC中,∠ACB=90°,△CAD≌△CED,△CEF≌△BEF,△CEF≌△CAD.
(1)求∠A,∠B的度数;
(2)猜想AC,EF的位置关系,并说明理由.
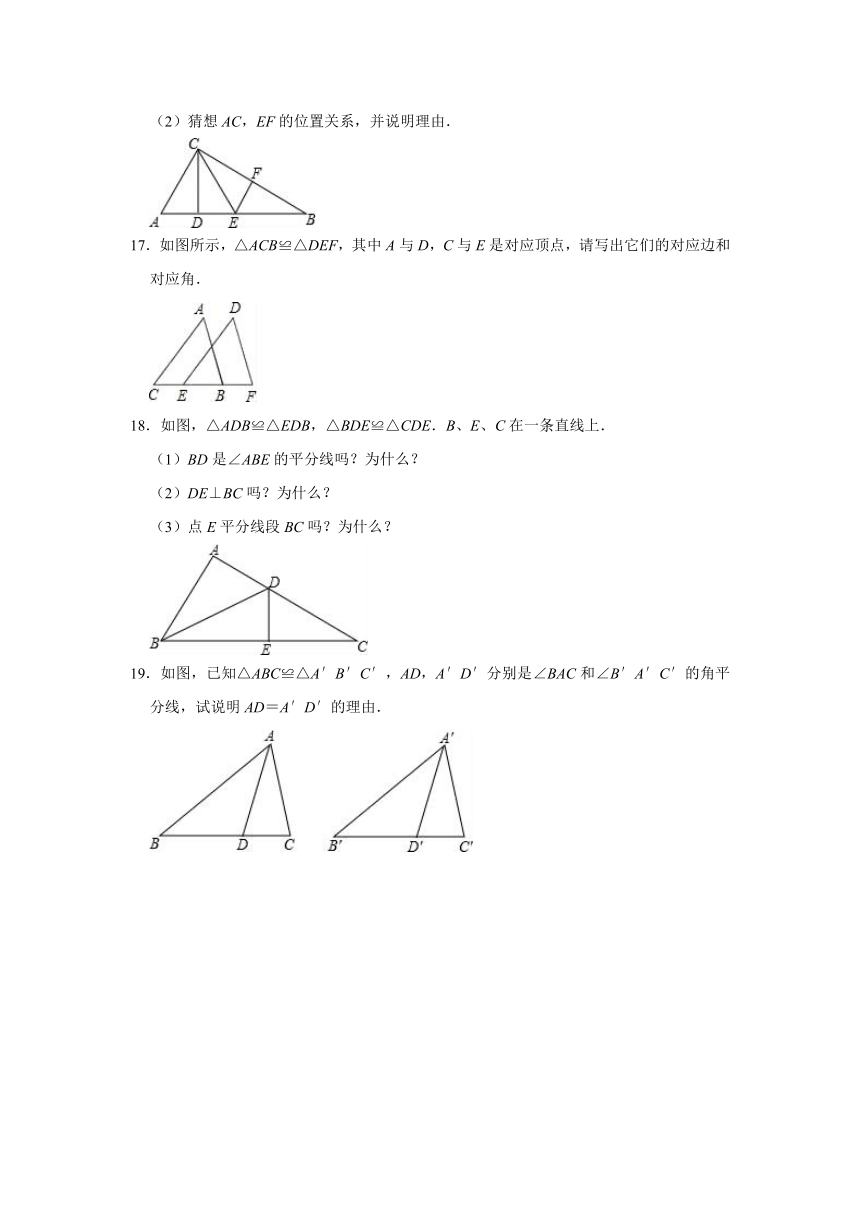
17.如图所示,△ACB≌△DEF,其中A与D,C与E是对应顶点,请写出它们的对应边和对应角.
18.如图,△ADB≌△EDB,△BDE≌△CDE.B、E、C在一条直线上.
(1)BD是∠ABE的平分线吗?为什么?
(2)DE⊥BC吗?为什么?
(3)点E平分线段BC吗?为什么?
19.如图,已知△ABC≌△A′B′C′,AD,A′D′分别是∠BAC和∠B′A′C′的角平分线,试说明AD=A′D′的理由.
参考答案与试题解析
一.选择题
1.【解答】解:∵△ABC≌△BAD,
∴AD=BC,
∵BC=5,
∴AD=5,
故选:B.
2.【解答】解:A、两个面积相等的圆一定全等,说法正确;
B、全等三角形是指形状、大小都相同的三角形,说法正确;
C、底边相等的两个等腰三角形全等,说法错误;
D、斜边上中线和一条直角边对应相等的两直角三角形全等,说法正确;
故选:C.
3.【解答】解:全等图形是指两个图形能够重合,
故选:A.
4.【解答】解:∵△ABC≌△EFD,
∴AC=DE,
∴AC﹣CD=DE﹣CD,
∴AD=CE,
∵AD+CD+CE=AE,AE=15,CD=3,
∴AD=CE=6,
∴AC=6+3=9,
故选:C.
5.【解答】解:∵△ABC≌△ADE,
∴∠B=∠ADE=60°,AB=AD,
∴∠ADB=∠B=60°,
∴∠EDC=180°﹣∠ADE﹣∠ADB=60°.
故选:C.
6.【解答】解:A、能够完全重合的两个图形叫做全等图形正确,故本选项正确;
B、周长相等的三角形是全等三角形错误,故本选项错误;
C、各角相等的三角形是全等三角形错误,故本选项错误;
D、面积相等的三角形是全等三角形错误,故本选项错误.
故选:A.
7.【解答】解:∵△ABD≌△ACE,
∴AB=AC,∠B=∠C,BD=CE,
∴BE=CD,
但不能得∠BAE=∠ADC.
故选:D.
8.【解答】解:∵△ABC≌△DEF,
∴∠B=∠DEF,
故选:C.
9.【解答】解:∵AD∥BC,∠C=90°,
∴∠D=180°﹣∠C=90°.
∵△ADF≌△AEB,
∴DF=EB,AD=AE,AF=AB,
∠AEB=∠D=90°,∠DAF=∠EAB,
∴A、B与C都正确,D错误.
故选:D.
10.【解答】解:∵△ABC≌△ADE,
∴∠C=∠AED=78°;
故选:D.
二.填空题(共5小题)
11.【解答】解:∵△ABC≌△DEF,
∴AB=DE,BC=EF,∠ACB=∠DFE.
12.【解答】解:∵△ABC≌△FDE,
∴AC=EF,
∴AE=FC,
∵AF=20,EC=10,
∴AE+FC=10,
∴AE=5.
故答案为:5.
13.【解答】解:如图两个全等三角形中,∠α=∠50°.
故答案是:50°.
14.【解答】解:如图,作AH、CK、FP分别垂直BC、AB、DE于H、K、P,
∴∠DPF=∠AKC=∠CHA=90°,
∵AB=BC,
∴∠BAC=∠BCA,
在△AKC和△CHA中,
,
∴△AKC≌△CHA(AAS),
∴KC=HA,
∵B、C两点在方程式y=﹣3的图形上,且A点的坐标为(﹣3,1),
∴AH=4,
∴KC=4,
∵△ABC≌△DEF,
∴∠BAC=∠EDF,AC=DF,
在△AKC和△DPF中,
,
∴△AKC≌△DPF(AAS),
∴KC=PF=4.
故答案为:4.
15.【解答】解:∵∠B=32°,∠A=68°
∴∠C=180°﹣32°﹣68°=80°
又△ABC≌△DEF
∴∠F=80度,DE=13cm.
三.解答题(共4小题)
16.【解答】解:(1)∵△CAD≌△CED,△CEF≌△CAD,
∴∠ADC=∠ACD=∠ECD,∠ECF=∠ACD,
∴∠ACB=∠ACD+∠ECD+∠ECF=3∠ECF=90°,
解得∠ECF=30°,
∵△CEF≌△BEF,
∴∠ECF=∠B=30°,
∴∠A=90°﹣∠B=60°;
(2)EF∥AC,理由如下:
∵△CEF≌△BEF,
∴∠CFE=∠BFE,
∵∠CFE+∠BFE=180°,
∴∠CFE=90°.
∴EF∥AC.
17.【解答】解:由△ACB和△DEF全等,可得:
AC的对应边是DE,BC的对应边是FE,AB的对应边是DF,∠ABC的对应角是∠DFE,∠A的对应角是∠D,∠ACB的对应角是∠DEF.
18.【解答】解:(1)BD是∠ABE的平分线,理由如下:
因为△ADB≌△EDB,
所以∠ABD=∠EBD,
即BD是∠ABE的平分线;
(2)DE⊥BC,理由如下:
因为△BDE≌△CDE,
所以BD=CD,BE=CE,
所以DE⊥BC;
(3)点E平分线段BC,理由如下:
因为△BDE≌△CDE,
所以BE=CE,
即点E平分线段BC.
19.【解答】证明:∵△ABC≌△A′B′C′,
∴AB=A′B′,∠B=∠B′,∠BAC=∠B′A′C′,
∵AD和A′D′分别是△ABC和△A′B′C′的角平分线,
∴∠BAD=∠BAC,∠B′A′D′=∠B′A′C′,
∴∠BAD=∠B′A′D′.
在△ABD和△A′B′D′中,
,
∴△ABD≌△A′B′D′(ASA),
∴AD=A′D′.
一.选择题
1.如图,△ABC≌△BAD,若AB=6,AC=4,BC=5,则AD的长为( )
A.4 B.5 C.6 D.以上都不对
2.下列说法错误的是( )
A.两个面积相等的圆一定全等
B.全等三角形是指形状、大小都相同的三角形
C.底边相等的两个等腰三角形全等
D.斜边上中线和一条直角边对应相等的两直角三角形全等
3.全等图形是指两个图形( )
A.能够重合 B.形状相同 C.大小相同 D.相等
4.如图,△ABC≌△EFD,AB=EF,AE=15,CD=3,则AC=( )
A.5 B.6 C.9 D.12
5.如图,△ABC≌△AED,点D落在BC上,且∠B=60°,则∠EDC的度数等于( )
A.45° B.30° C.60° D.75°
6.下列说法正确的是( )
A.能够完全重合的两个图形叫做全等图形
B.周长相等的三角形是全等三角形
C.各角相等的三角形是全等三角形
D.面积相等的三角形是全等三角形
7.如图,已知△ABD≌△ACE,则下列说法中不正确的是( )
A.AB=AC B.∠B=∠C C.BE=CD D.∠BAE=∠ADC
8.如图,已知△ABC与△DEF是全等三角形,则∠B=( )
A.∠F B.∠D C.∠DEF D.∠A
9.如图,在四边形ABCD中,AD∥BC,∠C=90°,点E,F分别在BC,CD上,若△ADF≌△AEB,则下列说法中不正确的是( )
A.DF=EB B.AE⊥BC C.∠DAF=∠EAB D.AB=AD
10.如图,已知△ABC≌△ADE,∠D=59°,∠AED=78°,则∠C的大小是( )
A.43° B.53° C.59° D.78°
二.填空题
11.若△ABC≌△DEF,此时 =DE,BC= ,∠ACB=∠ .
12.如图,△ABC≌△FDE,AB=FD,BC=DE,AF=20,EC=10,则AE的长是 .
13.如图两个全等三角形中,∠α的度数是 .
14.如图,直角坐标平面上,△ABC与△DEF全等,其中A,B,C的对应顶点分别为D,E,F,且AB=BC=5.若A点的坐标为(﹣3,1),B,C两点纵坐标都是﹣3,D,E两点在y轴上,则F点到y轴的距离为 .
15.如图,△ABC≌△DEF,A与D,B与E分别是对应顶点,∠B=32°,∠A=68°,AB=13cm,则∠F= 度,DE= cm.
三.解答题
16.如图,在△ABC中,∠ACB=90°,△CAD≌△CED,△CEF≌△BEF,△CEF≌△CAD.
(1)求∠A,∠B的度数;
(2)猜想AC,EF的位置关系,并说明理由.
17.如图所示,△ACB≌△DEF,其中A与D,C与E是对应顶点,请写出它们的对应边和对应角.
18.如图,△ADB≌△EDB,△BDE≌△CDE.B、E、C在一条直线上.
(1)BD是∠ABE的平分线吗?为什么?
(2)DE⊥BC吗?为什么?
(3)点E平分线段BC吗?为什么?
19.如图,已知△ABC≌△A′B′C′,AD,A′D′分别是∠BAC和∠B′A′C′的角平分线,试说明AD=A′D′的理由.
参考答案与试题解析
一.选择题
1.【解答】解:∵△ABC≌△BAD,
∴AD=BC,
∵BC=5,
∴AD=5,
故选:B.
2.【解答】解:A、两个面积相等的圆一定全等,说法正确;
B、全等三角形是指形状、大小都相同的三角形,说法正确;
C、底边相等的两个等腰三角形全等,说法错误;
D、斜边上中线和一条直角边对应相等的两直角三角形全等,说法正确;
故选:C.
3.【解答】解:全等图形是指两个图形能够重合,
故选:A.
4.【解答】解:∵△ABC≌△EFD,
∴AC=DE,
∴AC﹣CD=DE﹣CD,
∴AD=CE,
∵AD+CD+CE=AE,AE=15,CD=3,
∴AD=CE=6,
∴AC=6+3=9,
故选:C.
5.【解答】解:∵△ABC≌△ADE,
∴∠B=∠ADE=60°,AB=AD,
∴∠ADB=∠B=60°,
∴∠EDC=180°﹣∠ADE﹣∠ADB=60°.
故选:C.
6.【解答】解:A、能够完全重合的两个图形叫做全等图形正确,故本选项正确;
B、周长相等的三角形是全等三角形错误,故本选项错误;
C、各角相等的三角形是全等三角形错误,故本选项错误;
D、面积相等的三角形是全等三角形错误,故本选项错误.
故选:A.
7.【解答】解:∵△ABD≌△ACE,
∴AB=AC,∠B=∠C,BD=CE,
∴BE=CD,
但不能得∠BAE=∠ADC.
故选:D.
8.【解答】解:∵△ABC≌△DEF,
∴∠B=∠DEF,
故选:C.
9.【解答】解:∵AD∥BC,∠C=90°,
∴∠D=180°﹣∠C=90°.
∵△ADF≌△AEB,
∴DF=EB,AD=AE,AF=AB,
∠AEB=∠D=90°,∠DAF=∠EAB,
∴A、B与C都正确,D错误.
故选:D.
10.【解答】解:∵△ABC≌△ADE,
∴∠C=∠AED=78°;
故选:D.
二.填空题(共5小题)
11.【解答】解:∵△ABC≌△DEF,
∴AB=DE,BC=EF,∠ACB=∠DFE.
12.【解答】解:∵△ABC≌△FDE,
∴AC=EF,
∴AE=FC,
∵AF=20,EC=10,
∴AE+FC=10,
∴AE=5.
故答案为:5.
13.【解答】解:如图两个全等三角形中,∠α=∠50°.
故答案是:50°.
14.【解答】解:如图,作AH、CK、FP分别垂直BC、AB、DE于H、K、P,
∴∠DPF=∠AKC=∠CHA=90°,
∵AB=BC,
∴∠BAC=∠BCA,
在△AKC和△CHA中,
,
∴△AKC≌△CHA(AAS),
∴KC=HA,
∵B、C两点在方程式y=﹣3的图形上,且A点的坐标为(﹣3,1),
∴AH=4,
∴KC=4,
∵△ABC≌△DEF,
∴∠BAC=∠EDF,AC=DF,
在△AKC和△DPF中,
,
∴△AKC≌△DPF(AAS),
∴KC=PF=4.
故答案为:4.
15.【解答】解:∵∠B=32°,∠A=68°
∴∠C=180°﹣32°﹣68°=80°
又△ABC≌△DEF
∴∠F=80度,DE=13cm.
三.解答题(共4小题)
16.【解答】解:(1)∵△CAD≌△CED,△CEF≌△CAD,
∴∠ADC=∠ACD=∠ECD,∠ECF=∠ACD,
∴∠ACB=∠ACD+∠ECD+∠ECF=3∠ECF=90°,
解得∠ECF=30°,
∵△CEF≌△BEF,
∴∠ECF=∠B=30°,
∴∠A=90°﹣∠B=60°;
(2)EF∥AC,理由如下:
∵△CEF≌△BEF,
∴∠CFE=∠BFE,
∵∠CFE+∠BFE=180°,
∴∠CFE=90°.
∴EF∥AC.
17.【解答】解:由△ACB和△DEF全等,可得:
AC的对应边是DE,BC的对应边是FE,AB的对应边是DF,∠ABC的对应角是∠DFE,∠A的对应角是∠D,∠ACB的对应角是∠DEF.
18.【解答】解:(1)BD是∠ABE的平分线,理由如下:
因为△ADB≌△EDB,
所以∠ABD=∠EBD,
即BD是∠ABE的平分线;
(2)DE⊥BC,理由如下:
因为△BDE≌△CDE,
所以BD=CD,BE=CE,
所以DE⊥BC;
(3)点E平分线段BC,理由如下:
因为△BDE≌△CDE,
所以BE=CE,
即点E平分线段BC.
19.【解答】证明:∵△ABC≌△A′B′C′,
∴AB=A′B′,∠B=∠B′,∠BAC=∠B′A′C′,
∵AD和A′D′分别是△ABC和△A′B′C′的角平分线,
∴∠BAD=∠BAC,∠B′A′D′=∠B′A′C′,
∴∠BAD=∠B′A′D′.
在△ABD和△A′B′D′中,
,
∴△ABD≌△A′B′D′(ASA),
∴AD=A′D′.
