苏科版九年级下册数学 6.5相似三角形的性质 同步练习(word含解析)
文档属性
| 名称 | 苏科版九年级下册数学 6.5相似三角形的性质 同步练习(word含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 213.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-26 00:00:00 | ||
图片预览


文档简介
6.5相似三角形的性质
同步练习
一.选择题
1.如图,△OAB∽△OCD,OA:OC=3:2.△OAB与△OCD的面积分别是S1与S2,周长分别是C1与C2.则下列说法正确的是( )
A.=
B.=
C.=
D.=
2.如图,在△ABC中,点D在AB上,∠ACD=∠B.若AD=2,BD=3,则AC等于
( )
A.5
B.6
C.
D.
3.如图,AC⊥BC,AC:BC=3:4,D是AC上一点,连接BD,与∠ACB的平分线交于点E,连接AE,若S△ADE=,S△BCE=,则BC=( )
A.4
B.8
C.5
D.10
4.如图,在矩形ABCD中,AB=3,BC=10,点E在BC边上,DF⊥AE,垂足为F.若DF=6,则线段EF的长为( )
A.2
B.3
C.4
D.5
5.如图,在△ABC中,AB=AC=6,D是AC中点,E是BC上一点,BE=,∠AED=∠B,则CE的长为( )
A.
B.
C.
D.
6.已知两个相似三角形的面积之比为4:9,则这两个相似三角形的对应边之比是( )
A.16:81
B.4:9
C.9:4
D.2:3
7.如图,在平行四边形ABCD中,AD=BD=5,AB=6,E为AB的中点,F为CD上一点,连接EF交BD于点G,若S△FDG:S△EDG=2:3,则EF的长是( )
A.
B.2
C.2
D.5
8.在圆内接四边形ABCD中,∠ACB=∠ACD=60°,对角线AC、BD交于点E.已知BC=4,CD=2,则CE=( )
A.
B.
C.
D.
9.如图,在△ABC中,DE∥AC,AE、DC交于点F,则下列结论一定正确的是( )
A.
B.
C.
D.
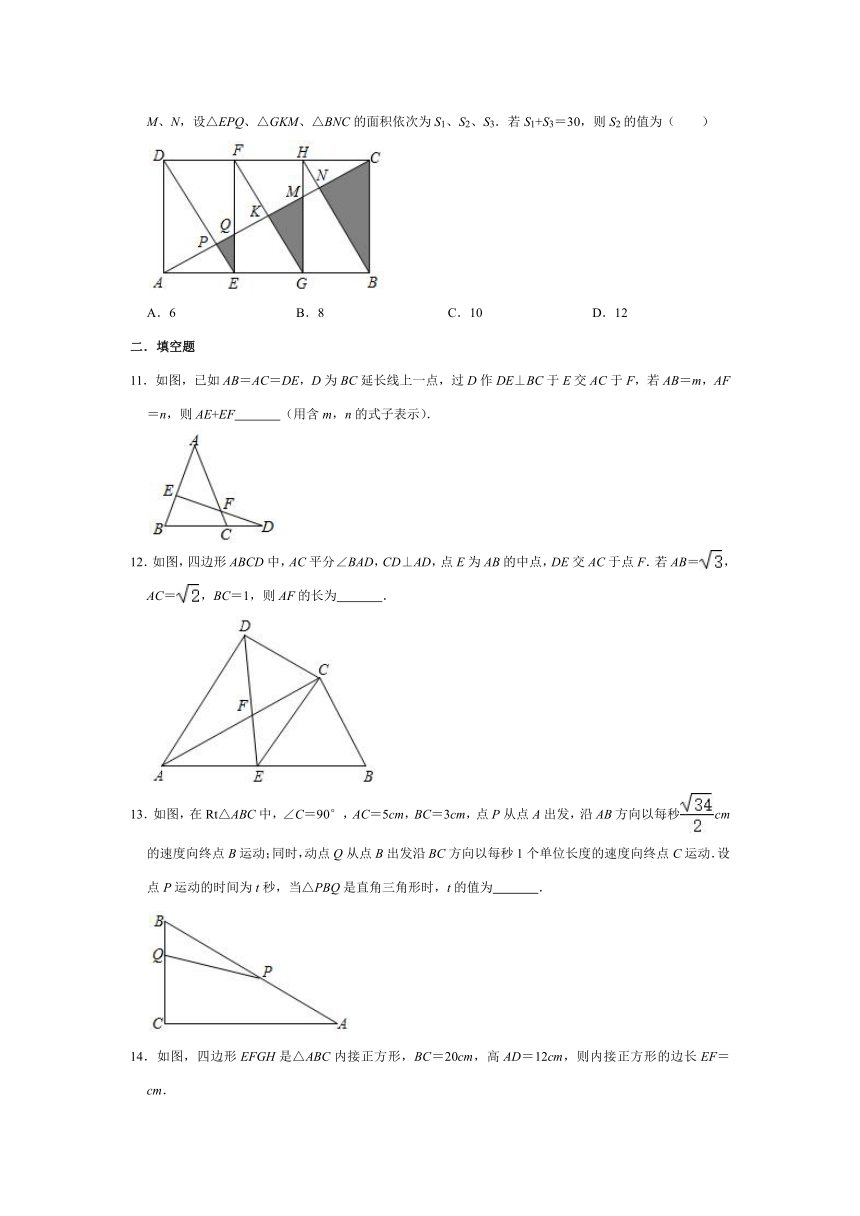
10.如图,矩形ABCD是由三个全等矩形拼成的,AC与DE、EF、FG、HG、HB分别交于点P、Q、K、M、N,设△EPQ、△GKM、△BNC的面积依次为S1、S2、S3.若S1+S3=30,则S2的值为( )
A.6
B.8
C.10
D.12
二.填空题
11.如图,已如AB=AC=DE,D为BC延长线上一点,过D作DE⊥BC于E交AC于F,若AB=m,AF=n,则AE+EF
(用含m,n的式子表示).
12.如图,四边形ABCD中,AC平分∠BAD,CD⊥AD,点E为AB的中点,DE交AC于点F.若AB=,AC=,BC=1,则AF的长为
.
13.如图,在Rt△ABC中,∠C=90°,AC=5cm,BC=3cm,点P从点A出发,沿AB方向以每秒cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1个单位长度的速度向终点C运动.设点P运动的时间为t秒,当△PBQ是直角三角形时,t的值为
.
14.如图,四边形EFGH是△ABC内接正方形,BC=20cm,高AD=12cm,则内接正方形的边长EF=
cm.
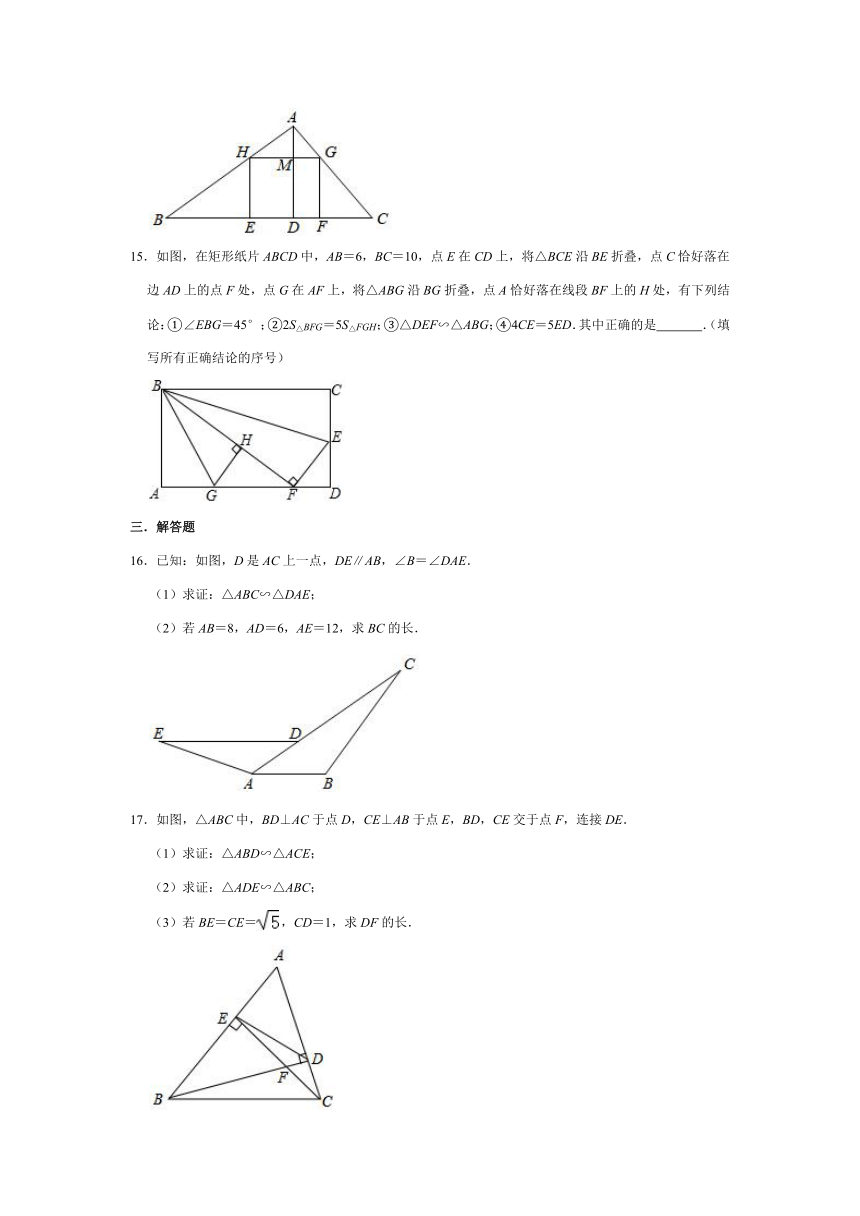
15.如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰好落在边AD上的点F处,点G在AF上,将△ABG沿BG折叠,点A恰好落在线段BF上的H处,有下列结论:①∠EBG=45°;②2S△BFG=5S△FGH;③△DEF∽△ABG;④4CE=5ED.其中正确的是
.(填写所有正确结论的序号)
三.解答题
16.已知:如图,D是AC上一点,DE∥AB,∠B=∠DAE.
(1)求证:△ABC∽△DAE;
(2)若AB=8,AD=6,AE=12,求BC的长.
17.如图,△ABC中,BD⊥AC于点D,CE⊥AB于点E,BD,CE交于点F,连接DE.
(1)求证:△ABD∽△ACE;
(2)求证:△ADE∽△ABC;
(3)若BE=CE=,CD=1,求DF的长.
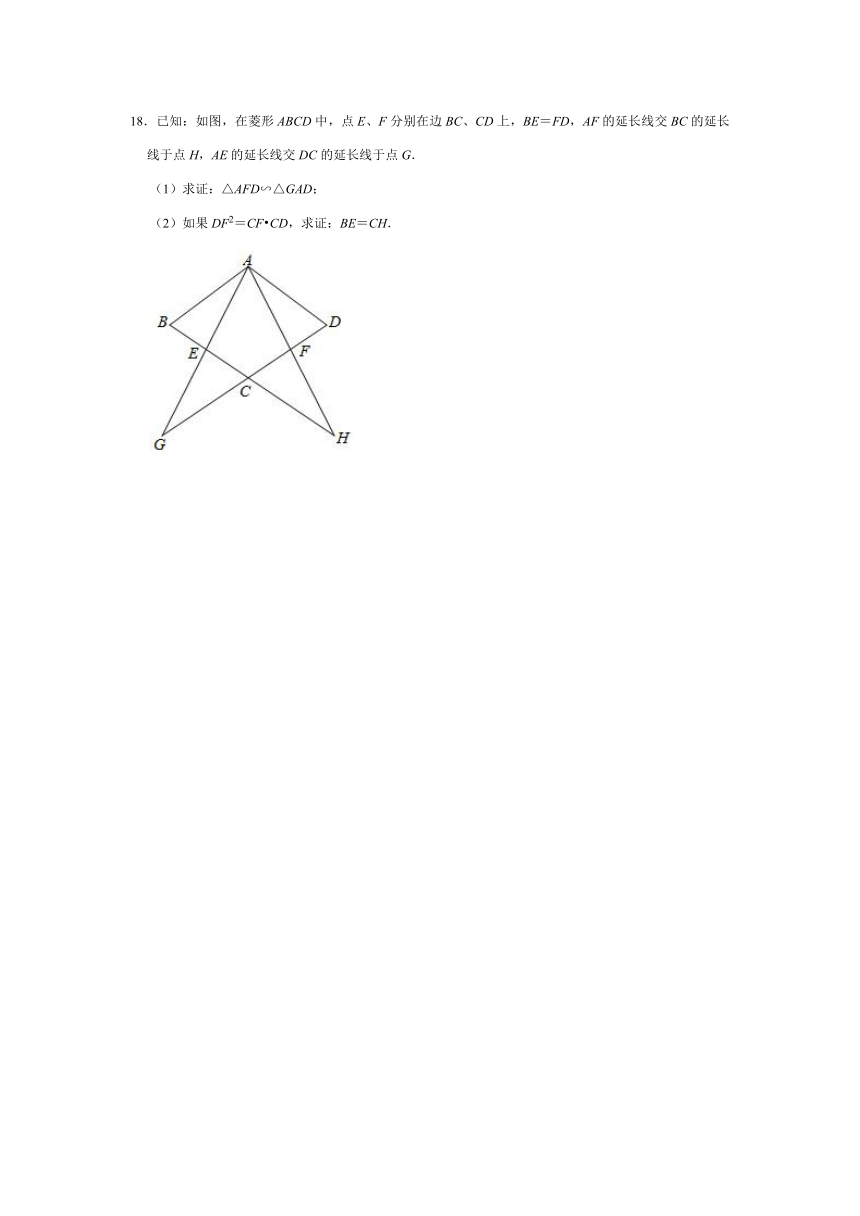
18.已知:如图,在菱形ABCD中,点E、F分别在边BC、CD上,BE=FD,AF的延长线交BC的延长线于点H,AE的延长线交DC的延长线于点G.
(1)求证:△AFD∽△GAD;
(2)如果DF2=CF?CD,求证:BE=CH.
参考答案
一.选择题
1.解:∵△OAB∽△OCD,OA:OC=3:2,
∴==,=()2=,
∴选项C正确,选项D错误,
∵无法确定,的值,故选项A,B错误,
故选:C.
2.解:在△ADC和△ACB中,
∵∠ACD=∠B,∠A=∠A,
∴△ADC∽△ACB,
∴AC:AB=AD:AC,
∴AC2=AB?AD,
∵AD=2,AB=AD+BD=2+3=5,
∴AC2=5×2=10,
∵AC>0,
∴AC=,
故选:D.
3.解:过点E作BC,AC的垂线,垂足分别为F,G,
设BC=4x,则AC=3x,
∵CE是∠ACB的平分线,EF⊥BC,EG⊥AC,
∴EF=EG,
又S△BCE=,S△ADE=,
∴AD=BC=x,
∴CD=2x,
∵四边形EFCG是正方形,
∴EF=FC,
∵EF∥CD,
∴△BEF∽△BDC,
∴=,即=,
解得,EF=x,
则×4x×x=,
解得,x=2,
则BC=4x=8,
故选:B.
4.解:∵四边形ABCD为矩形,
∴AB=CD=3,BC=AD=10,AD∥BC,
∴∠AEB=∠DAF,
∴△AFD∽△EBA,
∴,
∵DF=6,
∴AF==,
∴,
∴AE=5,
∴EF=AF﹣AE=8﹣5=3.
故选:B.
5.解:∵AB=AC,
∴∠B=∠C,
∵∠AEC=∠AED+∠DEC=∠B+∠BAE,∠AED=∠B,
∴∠DEC=∠BAE,
∴△BAE∽△CED,
∴=,
∵AB=AC=6,AD=DC=3,BE=,
∴=,
∴CE=,
故选:C.
6.解:∵相似三角形的面积的比等于相似比的平方.
∴两个相似三角形的面积之比为4:9时,
这两个相似三角形的对应边之比是2:3.
故选:D.
7.解:∵AD=BD,E为AB的中点,
∴DE⊥AB,AE=BE=AB=3,
∴DE===4,
∵S△FDG:S△EDG=2:3,
∴FG:EG=2:3,
∵AB∥CD,
∴△DFG∽△BEG,
∴==,
∴DF=2,
∵AB∥CD,DE⊥AB,
∴DE⊥CD,
∴EF===2.
故选:B.
8.解:∵∠ABD=∠ACD=60°,∠ADB=∠ACB=60°,
∴△ABD为等边三角形,
∴DA=DB,
在AC上截取AF=BC=4,如图,
在△ADF和△BCD中
,
∴△ADF≌△BCD(SAS),
∴DF=CD,
而∠DCF=60°,
∴△DCF为等边三角形,
∴CF=CD=2,
∴AC=AF+CF=4+2=6,
∵∠CBE=∠CAD,∠BCE=∠ACD,
∴△BCE∽△ACD,
∴BC:AC=CE:CD,即4:6=CE:2,
∴CE=.
故选:D.
9.解:∵DE∥AC
∴=,而AD是否等于BC不清楚,故A错误;
∵DE∥AC
∴△DEF∽△ACF
∴=,而FC未必等于FE,故B错误;
∵DE∥AC
∴△BDE∽△BAC
∴=
故C正确;
∵△DEF∽△ACF
∴=,无法得知的值是否等于,故D错误.
综上,只有C正确.
故选:C.
10.解:∵矩形ABCD是由三个全等矩形拼成,
∴△ADE≌△EFG≌△GHB,
∴∠AED=∠EGF=∠GBH,
∴∠DEF=∠FGH=∠HBC,
∵FE∥HG∥BC,
∴∠AQE=∠AMG=∠ACB,
∴△EPQ∽△GKM∽△BNC,
∵QE∥MG,
∴△AEQ∽△AGM,
∴==,
∴=()2=,
∴S1=S2,
∵MG∥CB,
∴△AGM∽△ABC,
∴==,
∴=()2=,
∴S3=S2,
∵S1+S3=30,
∴S2+S2=30,
∴S2=12.
故选:D.
二.填空题
11.解:过F点作FH∥AB交BD于H,
∴△DFH∽△DEB,∠B=∠FHC,
设AE=x,EF=y,则x2+y2=n2,
∵AB=AC,
∴∠B=∠ACB,
∴∠FHC=∠ACB,
∴FH=FC=m﹣n,
∵△DFH∽△DEB,
∴=,
∵AB=AC=DE,AB=m,AF=n,
∴=,
∴m(m﹣n)=(m﹣EF)(m﹣AE),
即m2﹣mn=m2﹣m(AE+EF)+AE×EF,
∵DE⊥BC,
∴∠DEA=90°,
∴n2=AE2+EF2,
∵(AE+EF)2=AE2+2AE×EF+EF2=n2+2AE×EF,
∴AE×EF=[(AE+EF)2﹣n2],
∴m2﹣mn=m2﹣m(AE+EF)+[(AE+EF)2﹣n2],
∴(AE+EF)2﹣2m(AE+EF)+2mn﹣n2=0,
(AE+EF﹣n)(AE+EF﹣2m+n)=0,
∴AE+EF=n,AE+EF=2m﹣n,
∵AE+EF=n时,AE+EF=(n2﹣n2)=0,不合题意舍去,
∴AE+EF=2m﹣n.
故答案为:=2m﹣n.
12.解:在△ACB中,AB=,AC=,BC=1,
∴()2=()2+12,
∴△ACB是直角三角形,即∠ACB=90°,
∵CD⊥AD,
∴∠ADC=90°,
∴∠ADC=∠ACB,
∵AC平分∠BAD,
∴∠DAC=∠CAB,
∴△ADC∽△ACB(AA),
∴=,即=,
解得AD=,
∵点E为AB的中点,
∴AE=CE=AB=,
∴∠ACE=∠CAB,
∴∠ACE=∠CAD,
∵∠AFD=∠CFE,
∴△FCE∽△FAD(AA),
∴===,
∴AF=AC=.
故答案为:.
13.解:在Rt△ABC中,∠C=90°,AC=5cm,BC=3cm,
∴AB==(cm).
由题意可知点P运动时间t秒时,AP=tcm,BQ=tcm,
∴BP=(﹣t)cm,BQ=tcm,
当△PBQ是直角三角形时,有两种情况:
①当∠BQ1P1=90°时,如图1:
∵∠C=90°,∠BQ1P1=90°,
∴∠C=∠BQ1P1,
又∵∠B=∠B,
∴△BQ1P1∽△BCA,
∴=,
∴=,
解得:t=;
②当∠BP2Q2=90°时,如图2:
∵∠C=90°,∠BP2Q2=90°,
∴∠C=∠BP2Q2,
又∵∠B=∠B,
∴△BP2Q2∽△BCA,
∴=,
∴=,
解得:t=.
故答案为:或.
14.解:设EF=xcm,则HG=MD=xcm,
∵四边形EFGH是△ABC内接正方形,
∴HG∥BC,
∴△AHG∽△ABC,
∴,
∵BC=20cm,高AD=12cm,
∴AM=(12﹣x)cm,
∴,
解得x=7.5,
即EF的长为7.5cm,
故答案为:7.5.
15.解:①由折叠的性质可知:∠CBE=∠FBE,∠ABG=∠FBG,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∴∠EBG=∠GBH+∠EBF=∠CBF+∠ABF=∠ABC=45°.
故①正确;
②由折叠的性质可知:BF=BC=10,BH=AB=6,
∴HF=BF﹣BH=4,
∴===,
∴2S△BFG=5S△FGH;
故②正确;
③∵四边形ABCD是矩形,
∴∠A=∠D=90°,
在Rt△ABF中,AF==8,
设GF=x,即HG=AG=8﹣x,
在Rt△HGF中,HG2+HF2=GF2,
即(8﹣x)2+42=x2,解得x=5,
∴AG=3,
∴FD=2;
同理可得ED=,
∴==2,
==,
∴≠,
∴△ABG与△DEF不相似,
故③错误;
④∵CD=AB=6,ED=,
∴CE=CD﹣ED=,
∴=,
∴4CE=5ED.
故④正确.
综上所述,正确的结论的序号为①②④.
三.解答题
16.解:(1)证明:∵DE∥AB,
∴∠EDA=∠CAB,
∵∠B=∠DAE,
∴△ABC∽△DAE;
(2)∵△ABC∽△DAE,
∴,
即,
∴BC=16.
17.(1)证明;∵BD⊥AC于点D,CE⊥AB于点E,
∴∠ADB=∠AEC=90°,
∵∠A=∠A,
∴△ADB∽△AEC.
(2)证明:∵△ADB∽△AEC,
∴=,
∴=,
∵∠A=∠A,
∴△ADE∽△ABC.
(3)解:过点E作EN⊥ED交BD于N,过点E作EM⊥DN于M.
在Rt△BEC中,∵BE=EC=,∠BEC=90°,
∴BC=BE=,∠BCF=45°,
∵∠BDC=90°,
∴BD===3,
∵∠EFB=∠DFC,∠BEF=∠CDF=90°,
∴△BFE∽△CFD,
∴=,
∴=,
∵∠EFD=∠BFC,
∴△EFD∽△BFC,
∴∠EDF=∠BCF=45°,
∵∠NED=90°,
∴∠END=∠EDN=45°,
∴EN=ED,
∵∠BEC=∠NED=90°,
∴∠BEN=∠CED,
∵BE=CE,
∴△BEN≌△CED(SAS),
∴BN=CD=1,DN=BD﹣BN=2,
∵EN=ED,EM⊥DN,
∴MN=DM=1,
∴EM=MN=MD=1,
∵∠EMF=∠CDF=90°,∠EFM=∠CFD,EM=CD,
∴△EMF≌△CDF(AAS),
∴MF=DF,
∴DF=.
18.(1)证明:∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D,
又∵BE=DF,
∴△ABE≌△ADF(SAS),
∴∠BAE=∠DAF.
∵AB∥CD,
∴∠G=∠BAE=∠DAF,
又∵∠D=∠D,
∴△AFD∽△GAD.
(2)证明:∵DF2=CF?CD,
∴=,
∵AD∥BH,
∴=,
∴=,
∵AD=CD,
∴CH=DF,
∵△ABE≌△ADF,
∴BE=DF,
∴BE=CH.
同步练习
一.选择题
1.如图,△OAB∽△OCD,OA:OC=3:2.△OAB与△OCD的面积分别是S1与S2,周长分别是C1与C2.则下列说法正确的是( )
A.=
B.=
C.=
D.=
2.如图,在△ABC中,点D在AB上,∠ACD=∠B.若AD=2,BD=3,则AC等于
( )
A.5
B.6
C.
D.
3.如图,AC⊥BC,AC:BC=3:4,D是AC上一点,连接BD,与∠ACB的平分线交于点E,连接AE,若S△ADE=,S△BCE=,则BC=( )
A.4
B.8
C.5
D.10
4.如图,在矩形ABCD中,AB=3,BC=10,点E在BC边上,DF⊥AE,垂足为F.若DF=6,则线段EF的长为( )
A.2
B.3
C.4
D.5
5.如图,在△ABC中,AB=AC=6,D是AC中点,E是BC上一点,BE=,∠AED=∠B,则CE的长为( )
A.
B.
C.
D.
6.已知两个相似三角形的面积之比为4:9,则这两个相似三角形的对应边之比是( )
A.16:81
B.4:9
C.9:4
D.2:3
7.如图,在平行四边形ABCD中,AD=BD=5,AB=6,E为AB的中点,F为CD上一点,连接EF交BD于点G,若S△FDG:S△EDG=2:3,则EF的长是( )
A.
B.2
C.2
D.5
8.在圆内接四边形ABCD中,∠ACB=∠ACD=60°,对角线AC、BD交于点E.已知BC=4,CD=2,则CE=( )
A.
B.
C.
D.
9.如图,在△ABC中,DE∥AC,AE、DC交于点F,则下列结论一定正确的是( )
A.
B.
C.
D.
10.如图,矩形ABCD是由三个全等矩形拼成的,AC与DE、EF、FG、HG、HB分别交于点P、Q、K、M、N,设△EPQ、△GKM、△BNC的面积依次为S1、S2、S3.若S1+S3=30,则S2的值为( )
A.6
B.8
C.10
D.12
二.填空题
11.如图,已如AB=AC=DE,D为BC延长线上一点,过D作DE⊥BC于E交AC于F,若AB=m,AF=n,则AE+EF
(用含m,n的式子表示).
12.如图,四边形ABCD中,AC平分∠BAD,CD⊥AD,点E为AB的中点,DE交AC于点F.若AB=,AC=,BC=1,则AF的长为
.
13.如图,在Rt△ABC中,∠C=90°,AC=5cm,BC=3cm,点P从点A出发,沿AB方向以每秒cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1个单位长度的速度向终点C运动.设点P运动的时间为t秒,当△PBQ是直角三角形时,t的值为
.
14.如图,四边形EFGH是△ABC内接正方形,BC=20cm,高AD=12cm,则内接正方形的边长EF=
cm.
15.如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰好落在边AD上的点F处,点G在AF上,将△ABG沿BG折叠,点A恰好落在线段BF上的H处,有下列结论:①∠EBG=45°;②2S△BFG=5S△FGH;③△DEF∽△ABG;④4CE=5ED.其中正确的是
.(填写所有正确结论的序号)
三.解答题
16.已知:如图,D是AC上一点,DE∥AB,∠B=∠DAE.
(1)求证:△ABC∽△DAE;
(2)若AB=8,AD=6,AE=12,求BC的长.
17.如图,△ABC中,BD⊥AC于点D,CE⊥AB于点E,BD,CE交于点F,连接DE.
(1)求证:△ABD∽△ACE;
(2)求证:△ADE∽△ABC;
(3)若BE=CE=,CD=1,求DF的长.
18.已知:如图,在菱形ABCD中,点E、F分别在边BC、CD上,BE=FD,AF的延长线交BC的延长线于点H,AE的延长线交DC的延长线于点G.
(1)求证:△AFD∽△GAD;
(2)如果DF2=CF?CD,求证:BE=CH.
参考答案
一.选择题
1.解:∵△OAB∽△OCD,OA:OC=3:2,
∴==,=()2=,
∴选项C正确,选项D错误,
∵无法确定,的值,故选项A,B错误,
故选:C.
2.解:在△ADC和△ACB中,
∵∠ACD=∠B,∠A=∠A,
∴△ADC∽△ACB,
∴AC:AB=AD:AC,
∴AC2=AB?AD,
∵AD=2,AB=AD+BD=2+3=5,
∴AC2=5×2=10,
∵AC>0,
∴AC=,
故选:D.
3.解:过点E作BC,AC的垂线,垂足分别为F,G,
设BC=4x,则AC=3x,
∵CE是∠ACB的平分线,EF⊥BC,EG⊥AC,
∴EF=EG,
又S△BCE=,S△ADE=,
∴AD=BC=x,
∴CD=2x,
∵四边形EFCG是正方形,
∴EF=FC,
∵EF∥CD,
∴△BEF∽△BDC,
∴=,即=,
解得,EF=x,
则×4x×x=,
解得,x=2,
则BC=4x=8,
故选:B.
4.解:∵四边形ABCD为矩形,
∴AB=CD=3,BC=AD=10,AD∥BC,
∴∠AEB=∠DAF,
∴△AFD∽△EBA,
∴,
∵DF=6,
∴AF==,
∴,
∴AE=5,
∴EF=AF﹣AE=8﹣5=3.
故选:B.
5.解:∵AB=AC,
∴∠B=∠C,
∵∠AEC=∠AED+∠DEC=∠B+∠BAE,∠AED=∠B,
∴∠DEC=∠BAE,
∴△BAE∽△CED,
∴=,
∵AB=AC=6,AD=DC=3,BE=,
∴=,
∴CE=,
故选:C.
6.解:∵相似三角形的面积的比等于相似比的平方.
∴两个相似三角形的面积之比为4:9时,
这两个相似三角形的对应边之比是2:3.
故选:D.
7.解:∵AD=BD,E为AB的中点,
∴DE⊥AB,AE=BE=AB=3,
∴DE===4,
∵S△FDG:S△EDG=2:3,
∴FG:EG=2:3,
∵AB∥CD,
∴△DFG∽△BEG,
∴==,
∴DF=2,
∵AB∥CD,DE⊥AB,
∴DE⊥CD,
∴EF===2.
故选:B.
8.解:∵∠ABD=∠ACD=60°,∠ADB=∠ACB=60°,
∴△ABD为等边三角形,
∴DA=DB,
在AC上截取AF=BC=4,如图,
在△ADF和△BCD中
,
∴△ADF≌△BCD(SAS),
∴DF=CD,
而∠DCF=60°,
∴△DCF为等边三角形,
∴CF=CD=2,
∴AC=AF+CF=4+2=6,
∵∠CBE=∠CAD,∠BCE=∠ACD,
∴△BCE∽△ACD,
∴BC:AC=CE:CD,即4:6=CE:2,
∴CE=.
故选:D.
9.解:∵DE∥AC
∴=,而AD是否等于BC不清楚,故A错误;
∵DE∥AC
∴△DEF∽△ACF
∴=,而FC未必等于FE,故B错误;
∵DE∥AC
∴△BDE∽△BAC
∴=
故C正确;
∵△DEF∽△ACF
∴=,无法得知的值是否等于,故D错误.
综上,只有C正确.
故选:C.
10.解:∵矩形ABCD是由三个全等矩形拼成,
∴△ADE≌△EFG≌△GHB,
∴∠AED=∠EGF=∠GBH,
∴∠DEF=∠FGH=∠HBC,
∵FE∥HG∥BC,
∴∠AQE=∠AMG=∠ACB,
∴△EPQ∽△GKM∽△BNC,
∵QE∥MG,
∴△AEQ∽△AGM,
∴==,
∴=()2=,
∴S1=S2,
∵MG∥CB,
∴△AGM∽△ABC,
∴==,
∴=()2=,
∴S3=S2,
∵S1+S3=30,
∴S2+S2=30,
∴S2=12.
故选:D.
二.填空题
11.解:过F点作FH∥AB交BD于H,
∴△DFH∽△DEB,∠B=∠FHC,
设AE=x,EF=y,则x2+y2=n2,
∵AB=AC,
∴∠B=∠ACB,
∴∠FHC=∠ACB,
∴FH=FC=m﹣n,
∵△DFH∽△DEB,
∴=,
∵AB=AC=DE,AB=m,AF=n,
∴=,
∴m(m﹣n)=(m﹣EF)(m﹣AE),
即m2﹣mn=m2﹣m(AE+EF)+AE×EF,
∵DE⊥BC,
∴∠DEA=90°,
∴n2=AE2+EF2,
∵(AE+EF)2=AE2+2AE×EF+EF2=n2+2AE×EF,
∴AE×EF=[(AE+EF)2﹣n2],
∴m2﹣mn=m2﹣m(AE+EF)+[(AE+EF)2﹣n2],
∴(AE+EF)2﹣2m(AE+EF)+2mn﹣n2=0,
(AE+EF﹣n)(AE+EF﹣2m+n)=0,
∴AE+EF=n,AE+EF=2m﹣n,
∵AE+EF=n时,AE+EF=(n2﹣n2)=0,不合题意舍去,
∴AE+EF=2m﹣n.
故答案为:=2m﹣n.
12.解:在△ACB中,AB=,AC=,BC=1,
∴()2=()2+12,
∴△ACB是直角三角形,即∠ACB=90°,
∵CD⊥AD,
∴∠ADC=90°,
∴∠ADC=∠ACB,
∵AC平分∠BAD,
∴∠DAC=∠CAB,
∴△ADC∽△ACB(AA),
∴=,即=,
解得AD=,
∵点E为AB的中点,
∴AE=CE=AB=,
∴∠ACE=∠CAB,
∴∠ACE=∠CAD,
∵∠AFD=∠CFE,
∴△FCE∽△FAD(AA),
∴===,
∴AF=AC=.
故答案为:.
13.解:在Rt△ABC中,∠C=90°,AC=5cm,BC=3cm,
∴AB==(cm).
由题意可知点P运动时间t秒时,AP=tcm,BQ=tcm,
∴BP=(﹣t)cm,BQ=tcm,
当△PBQ是直角三角形时,有两种情况:
①当∠BQ1P1=90°时,如图1:
∵∠C=90°,∠BQ1P1=90°,
∴∠C=∠BQ1P1,
又∵∠B=∠B,
∴△BQ1P1∽△BCA,
∴=,
∴=,
解得:t=;
②当∠BP2Q2=90°时,如图2:
∵∠C=90°,∠BP2Q2=90°,
∴∠C=∠BP2Q2,
又∵∠B=∠B,
∴△BP2Q2∽△BCA,
∴=,
∴=,
解得:t=.
故答案为:或.
14.解:设EF=xcm,则HG=MD=xcm,
∵四边形EFGH是△ABC内接正方形,
∴HG∥BC,
∴△AHG∽△ABC,
∴,
∵BC=20cm,高AD=12cm,
∴AM=(12﹣x)cm,
∴,
解得x=7.5,
即EF的长为7.5cm,
故答案为:7.5.
15.解:①由折叠的性质可知:∠CBE=∠FBE,∠ABG=∠FBG,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∴∠EBG=∠GBH+∠EBF=∠CBF+∠ABF=∠ABC=45°.
故①正确;
②由折叠的性质可知:BF=BC=10,BH=AB=6,
∴HF=BF﹣BH=4,
∴===,
∴2S△BFG=5S△FGH;
故②正确;
③∵四边形ABCD是矩形,
∴∠A=∠D=90°,
在Rt△ABF中,AF==8,
设GF=x,即HG=AG=8﹣x,
在Rt△HGF中,HG2+HF2=GF2,
即(8﹣x)2+42=x2,解得x=5,
∴AG=3,
∴FD=2;
同理可得ED=,
∴==2,
==,
∴≠,
∴△ABG与△DEF不相似,
故③错误;
④∵CD=AB=6,ED=,
∴CE=CD﹣ED=,
∴=,
∴4CE=5ED.
故④正确.
综上所述,正确的结论的序号为①②④.
三.解答题
16.解:(1)证明:∵DE∥AB,
∴∠EDA=∠CAB,
∵∠B=∠DAE,
∴△ABC∽△DAE;
(2)∵△ABC∽△DAE,
∴,
即,
∴BC=16.
17.(1)证明;∵BD⊥AC于点D,CE⊥AB于点E,
∴∠ADB=∠AEC=90°,
∵∠A=∠A,
∴△ADB∽△AEC.
(2)证明:∵△ADB∽△AEC,
∴=,
∴=,
∵∠A=∠A,
∴△ADE∽△ABC.
(3)解:过点E作EN⊥ED交BD于N,过点E作EM⊥DN于M.
在Rt△BEC中,∵BE=EC=,∠BEC=90°,
∴BC=BE=,∠BCF=45°,
∵∠BDC=90°,
∴BD===3,
∵∠EFB=∠DFC,∠BEF=∠CDF=90°,
∴△BFE∽△CFD,
∴=,
∴=,
∵∠EFD=∠BFC,
∴△EFD∽△BFC,
∴∠EDF=∠BCF=45°,
∵∠NED=90°,
∴∠END=∠EDN=45°,
∴EN=ED,
∵∠BEC=∠NED=90°,
∴∠BEN=∠CED,
∵BE=CE,
∴△BEN≌△CED(SAS),
∴BN=CD=1,DN=BD﹣BN=2,
∵EN=ED,EM⊥DN,
∴MN=DM=1,
∴EM=MN=MD=1,
∵∠EMF=∠CDF=90°,∠EFM=∠CFD,EM=CD,
∴△EMF≌△CDF(AAS),
∴MF=DF,
∴DF=.
18.(1)证明:∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D,
又∵BE=DF,
∴△ABE≌△ADF(SAS),
∴∠BAE=∠DAF.
∵AB∥CD,
∴∠G=∠BAE=∠DAF,
又∵∠D=∠D,
∴△AFD∽△GAD.
(2)证明:∵DF2=CF?CD,
∴=,
∵AD∥BH,
∴=,
∴=,
∵AD=CD,
∴CH=DF,
∵△ABE≌△ADF,
∴BE=DF,
∴BE=CH.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
