人教版八年级数学 下册课件:18.1.2-2平行四边形的判定(第二课时 共18张PPT)
文档属性
| 名称 | 人教版八年级数学 下册课件:18.1.2-2平行四边形的判定(第二课时 共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 304.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-26 23:09:43 | ||
图片预览





文档简介
18.1.2
平行四边形的判定
第2课时
第十八章
平行四边形
18.1
平行四边形
课前预习:课本46----47
预习目标:
1、我们学行四边形哪些判定方法?
2、还有其他的判定方法吗?
3、猜想其它判定方法并证明。
4、平行四边形判定方法的应用。
5、总结
活动一:温故知新,引入新课
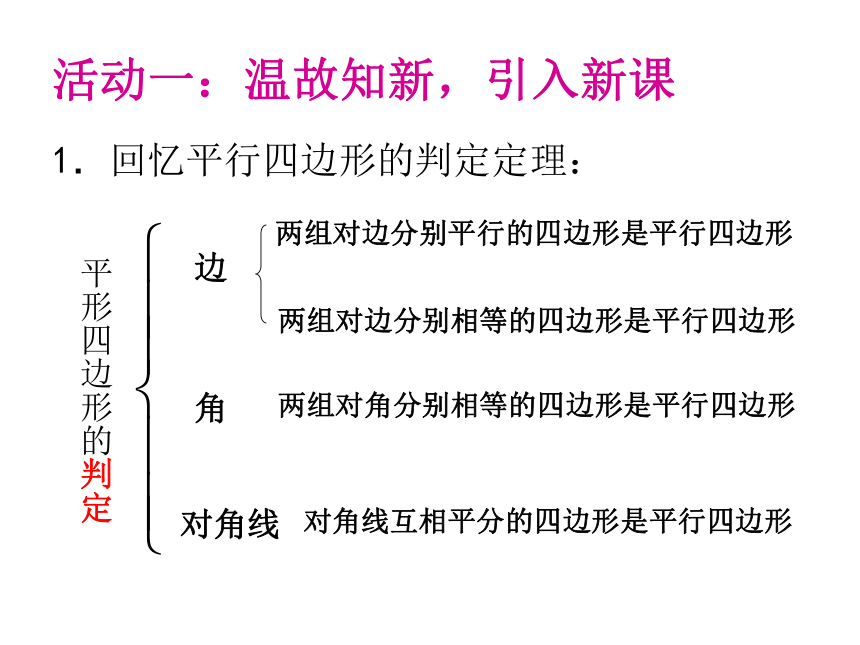
1.回忆平行四边形的判定定理:
平形四边形的判定
两组对边分别平行的四边形是平行四边形
边
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
角
对角线
2.思考问题,引入新课.
以小组讨论的形式探讨这一问题.
我们知道两组对边分别平行或相等的四边形是平行四边形.
请同学们猜想一下,如果只考虑四边形的一组对边,当它满足什么条件时这个四边形是平行四边形?
问题1:一组对边平行的四边形是平行四边形吗?如果是请给出证明,如果不是请举出反例说明.
活动二:猜想证明,探索新知
小学学习过的梯形满足一组对边平行的条件,但梯形不是平行四边形.
问题2:满足一组对边相等的四边形是平行四边形吗?
如图1
,这个四边形EFGH满足一组对边EF=HG相等的条件,但它不是平行四边形.
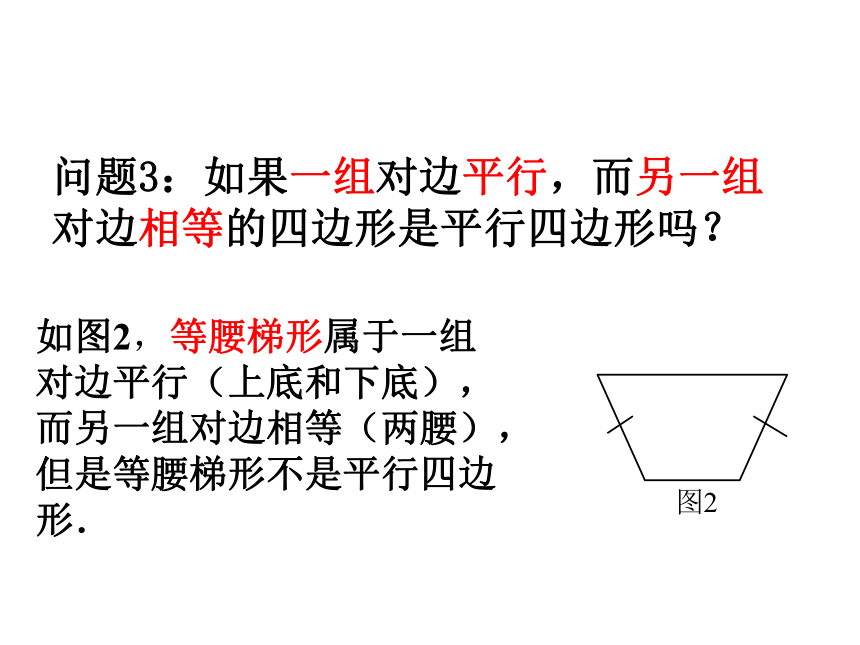
问题3:如果一组对边平行,而另一组对边相等的四边形是平行四边形吗?
如图2,等腰梯形属于一组对边平行(上底和下底),而另一组对边相等(两腰),但是等腰梯形不是平行四边形.
图2
请你猜想,这个命题成立吗?若成立,写出证明方法。
命题:一组对边平行且相等的四边形是平行四边形.
命题:一组对边平行且相等的四边形是平行四边形.
请你将上述命题改写成已知、求证,并画出图形,然后思考如何证明.
图3
已知:如图3
,在四边
形ABCD中,AB//CD,
AB=CD.
求证:四边形ABCD是
平行四边形.
已知:如图,在四边形ABCD中,AB//CD,
AB=CD,
求证:四边形ABCD是平行四边形.
证明:方法1:如图,
连接
AC.
∵AB
//CD
,
∴∠1=∠2.
又
∵AB
=CD
,
AC
=CA
,
∴△ABC≌△CDA.
∴BC
=DA
.
∴四边形ABCD是平行四边形.
方法2:
∵AB
//CD
,
∴∠1=∠2
.
又
∵AB
=CD
,
AC
=CA
,
∴△ABC≌△CDA
.
∴∠BCA=∠DAC
.
∴AD
//BC
.
∴四边形ABCD是平行四边形.
如图,连接
AC.
平行四边形的判定定理:
一组对边平行且相等的四边形是平行四边形.
在四边形ABCD中,
∵AB//CD,AB
=CD,
∴四边形ABCD是平行四边形.
符号语言:
强调:同一组对边平行且相等.
活动三:归纳定理
活动四:学以致用
为了保证铁路的两条直铺的铁轨互相平行,只要使互相平行的夹在铁轨之间的枕木长相等就可以了.你能说出其中的道理吗?
贴上图片
证明:
∵四边形ABCD是平行四边形,
∴AB
=CD,EB
//FD.
又
∵EB
=
AB
,FD
=
CD,
∴EB
=FD
.
∴四边形EBFD是平行四边形.
例
如图
,在平行四边形ABCD中,E,F分别是AB,CD的中点.
求证:四边形EBFD是平行四边形.
2.
已知:如图,在四边形
ABCD中,对角线AC和BD相交于O,AO=OC,BA⊥AC,DC⊥AC.
求证:四边形ABCD是平行四边形.
活动五:应用新知,巩固提高
1.教材第47页练习第4题.
Z````x``xk
习题18.1第4、6题.
活动六:课堂检测
两组对边分别平行的四边形是平行四边形
平形四边形的判定
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
边
角
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
对角线
判定一个四边形是平行四边形的方法:
活动七:总结
1.本节课你学习了哪些知识?
2.你获得了哪些研究问题的方法?
3.你有什么收获?
平行四边形的判定
第2课时
第十八章
平行四边形
18.1
平行四边形
课前预习:课本46----47
预习目标:
1、我们学行四边形哪些判定方法?
2、还有其他的判定方法吗?
3、猜想其它判定方法并证明。
4、平行四边形判定方法的应用。
5、总结
活动一:温故知新,引入新课
1.回忆平行四边形的判定定理:
平形四边形的判定
两组对边分别平行的四边形是平行四边形
边
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
角
对角线
2.思考问题,引入新课.
以小组讨论的形式探讨这一问题.
我们知道两组对边分别平行或相等的四边形是平行四边形.
请同学们猜想一下,如果只考虑四边形的一组对边,当它满足什么条件时这个四边形是平行四边形?
问题1:一组对边平行的四边形是平行四边形吗?如果是请给出证明,如果不是请举出反例说明.
活动二:猜想证明,探索新知
小学学习过的梯形满足一组对边平行的条件,但梯形不是平行四边形.
问题2:满足一组对边相等的四边形是平行四边形吗?
如图1
,这个四边形EFGH满足一组对边EF=HG相等的条件,但它不是平行四边形.
问题3:如果一组对边平行,而另一组对边相等的四边形是平行四边形吗?
如图2,等腰梯形属于一组对边平行(上底和下底),而另一组对边相等(两腰),但是等腰梯形不是平行四边形.
图2
请你猜想,这个命题成立吗?若成立,写出证明方法。
命题:一组对边平行且相等的四边形是平行四边形.
命题:一组对边平行且相等的四边形是平行四边形.
请你将上述命题改写成已知、求证,并画出图形,然后思考如何证明.
图3
已知:如图3
,在四边
形ABCD中,AB//CD,
AB=CD.
求证:四边形ABCD是
平行四边形.
已知:如图,在四边形ABCD中,AB//CD,
AB=CD,
求证:四边形ABCD是平行四边形.
证明:方法1:如图,
连接
AC.
∵AB
//CD
,
∴∠1=∠2.
又
∵AB
=CD
,
AC
=CA
,
∴△ABC≌△CDA.
∴BC
=DA
.
∴四边形ABCD是平行四边形.
方法2:
∵AB
//CD
,
∴∠1=∠2
.
又
∵AB
=CD
,
AC
=CA
,
∴△ABC≌△CDA
.
∴∠BCA=∠DAC
.
∴AD
//BC
.
∴四边形ABCD是平行四边形.
如图,连接
AC.
平行四边形的判定定理:
一组对边平行且相等的四边形是平行四边形.
在四边形ABCD中,
∵AB//CD,AB
=CD,
∴四边形ABCD是平行四边形.
符号语言:
强调:同一组对边平行且相等.
活动三:归纳定理
活动四:学以致用
为了保证铁路的两条直铺的铁轨互相平行,只要使互相平行的夹在铁轨之间的枕木长相等就可以了.你能说出其中的道理吗?
贴上图片
证明:
∵四边形ABCD是平行四边形,
∴AB
=CD,EB
//FD.
又
∵EB
=
AB
,FD
=
CD,
∴EB
=FD
.
∴四边形EBFD是平行四边形.
例
如图
,在平行四边形ABCD中,E,F分别是AB,CD的中点.
求证:四边形EBFD是平行四边形.
2.
已知:如图,在四边形
ABCD中,对角线AC和BD相交于O,AO=OC,BA⊥AC,DC⊥AC.
求证:四边形ABCD是平行四边形.
活动五:应用新知,巩固提高
1.教材第47页练习第4题.
Z````x``xk
习题18.1第4、6题.
活动六:课堂检测
两组对边分别平行的四边形是平行四边形
平形四边形的判定
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
边
角
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
对角线
判定一个四边形是平行四边形的方法:
活动七:总结
1.本节课你学习了哪些知识?
2.你获得了哪些研究问题的方法?
3.你有什么收获?
